Приведение подобных слагаемых
Чтобы привести подобные слагаемые с помощью меню:
1. Ввести выражение.
2. Выделить в выражении имя переменной, относительно которой надо привести подобные слагаемые.
3. Выберите команду Symbolics/Collect (Символика/Привести подобные).
Также эту операцию можно выполнить с помощью оператора символьного вывода и ключевого слова collect.
Разложение на элементарные дроби
Чтобы разложить сложную дробь на более простые дроби, следует либо выполнить команду Symbolics/Variable/Convert to Partial Fractions (Символика/Переменная/Разложить на элементарные дроби), либо указать ключевое слово parfrac. Применяя первый способ необходимо перед выбором команды выделить переменную, относительно которой будет производиться разложение (см.рис.5).
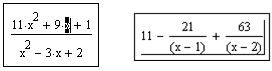
Рис.5. Разложение сложной дроби на элементарные дроби
Интегрирование
Интегрирование в Mathcad реализовано в виде вычислительного оператора. Для вычисления неопределенного интеграла от некоторого выражения по определенной переменной выделите в выражении переменную и выполните команду Symbolics/Variable/Integrate (Символика/Переменная/Интегрировать). Вычисленное аналитическое представление неопределенного интеграла появиться ниже.
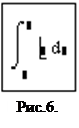 Чтобы вычислить определенный интеграл, следует напечатать его обычную математическую форму в документе. Делается это с помощью панели Calculus (Вычисления) нажатием кнопки со значком интеграла или вводом с клавиатуры сочетания клавиш <Shift>+<7>. Появится символ интеграла с несколькими местозаполнителями (рис.6), в которые нужно ввести нижний и верхний интервалы интегрирования, подынтегральную функцию и переменную интегрирования. Чтобы получить результат интегрирования, следует ввести знак равенства (=) или символьного равенства (®).
Чтобы вычислить определенный интеграл, следует напечатать его обычную математическую форму в документе. Делается это с помощью панели Calculus (Вычисления) нажатием кнопки со значком интеграла или вводом с клавиатуры сочетания клавиш <Shift>+<7>. Появится символ интеграла с несколькими местозаполнителями (рис.6), в которые нужно ввести нижний и верхний интервалы интегрирования, подынтегральную функцию и переменную интегрирования. Чтобы получить результат интегрирования, следует ввести знак равенства (=) или символьного равенства (®).
Дифференцирование
 С помощью Mathcad можно вычислять производные скалярных функций любого количества аргументов, от 0-го до 5-го порядка включительно. И функции, и аргументы могут быть как действительными, так и комплексными.
С помощью Mathcad можно вычислять производные скалярных функций любого количества аргументов, от 0-го до 5-го порядка включительно. И функции, и аргументы могут быть как действительными, так и комплексными.
Для того чтобы продифференцировать функцию f(x) необходимо:
1. Ввести оператор дифференцирования нажатием кнопки Derivative (Производная) на панели Calculus (Вычисления) или введите с клавиатуры вопросительный знак <?>,
2.  В появившихся местозаполнителях (рис.7) ввести функцию f(x) и имя самого аргумента x.
В появившихся местозаполнителях (рис.7) ввести функцию f(x) и имя самого аргумента x.
3. Ввести оператор (®) символьного вывода для получении ответа.
Чтобы вычислить производную n-го порядка, нужно проделать те же самые действия, что и при взятии первой производной, за тем исключением, что вместо оператора первой производной необходимо применить оператор n-й производной – NthDerivative на панели Calculus (Вычисления) или нажать сочетание клавиш <Ctrl>+<?>.
Решение уравнений
Рассмотрим алгебраическое уравнение f(x)=0. Данное уравнение можно решить двумя способами:
I. способ:
1. Ввести выражение f(x);
2. Выделить переменную, относительно которой будет решаться уравнение, приравнивающее выражение к нулю - х;
3. Выбрать в меню Symbolics (Символика) пункт Variable / Solve (Переменная/Решить).
II. способ:
Щелкните по кнопке решения уравнений solve в панели символьных вычислений Symbolic. Введите в местозаполнитель слева от ключевого словаsolve (решить) выражение для правой части уравнения, а в позиции справа отsolve (решить) — имя переменной, относительно которой нужно решить уравнение, и щелкните по свободному месту в рабочем документе. Результат — значение корня уравнения — будет отображен в рабочем документе справа от стрелки
