Закон распределения Пуассона

Если число испытаний увеличивается, то увеличивается число и членов биномиального распределения. Так как сумма вероятностей всех возможных значений остается равной единице, то значение вероятности каждого отдельного значения уменьшается. Этим объясняется то, что закон Пуассона иногда называют законом редких событий.

Определение. Дискретная случайная величина , возможными значениями которой являются 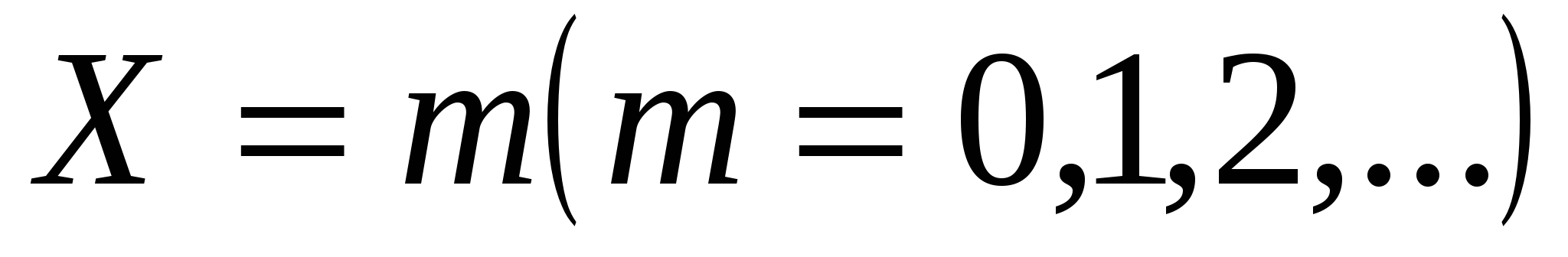, а вероятности соответствующих значений определяются по формуле Пуассона

,

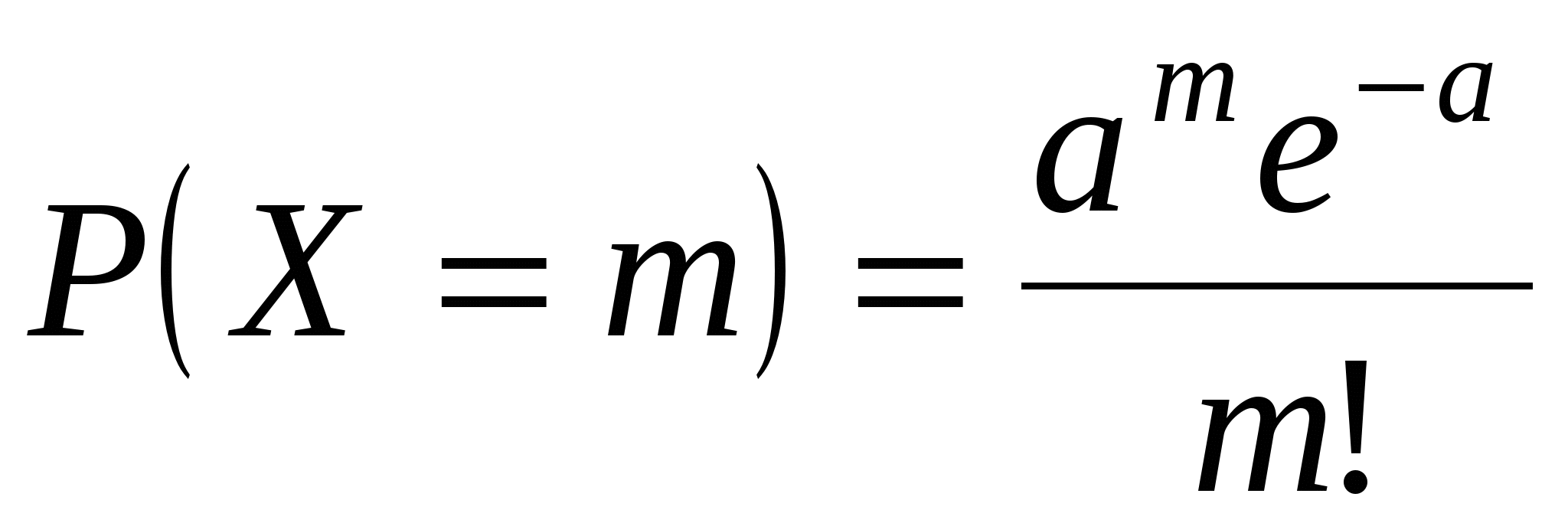называется пуассоновской случайной величинойс параметром .

Пуассоновское распределение широко используется в теории массового обслуживания. Число называется интенсивностью.

Закон распределения Пуассона случайной величины можно записать в виде таблицы 2:

Таблица 2.

				…		…
				…		…

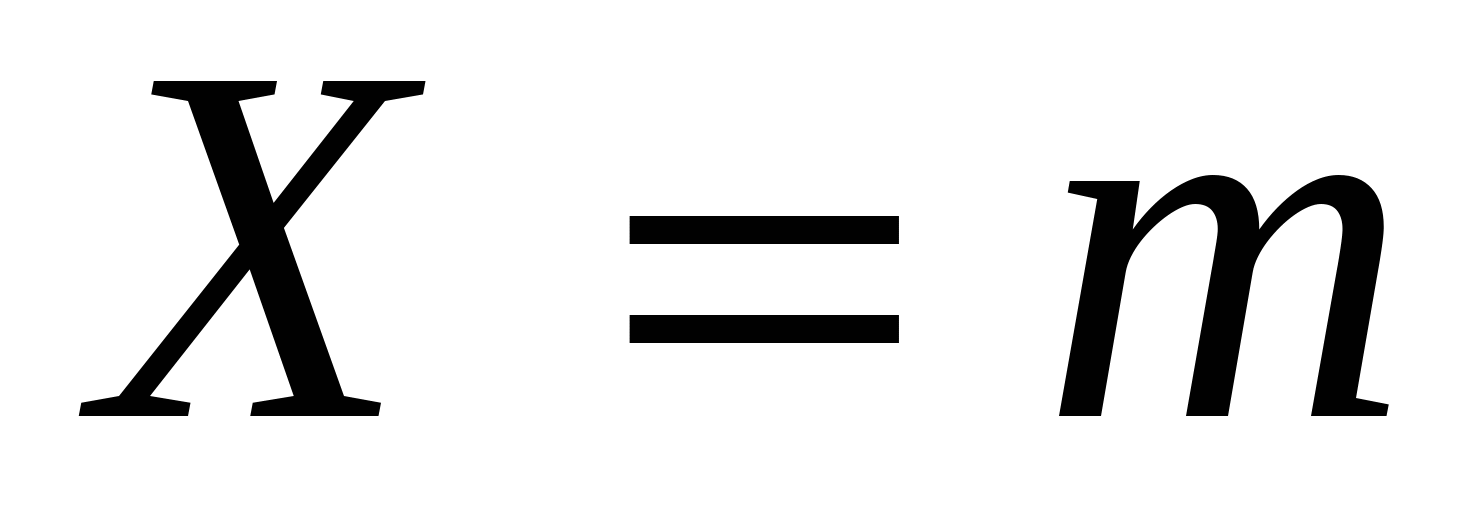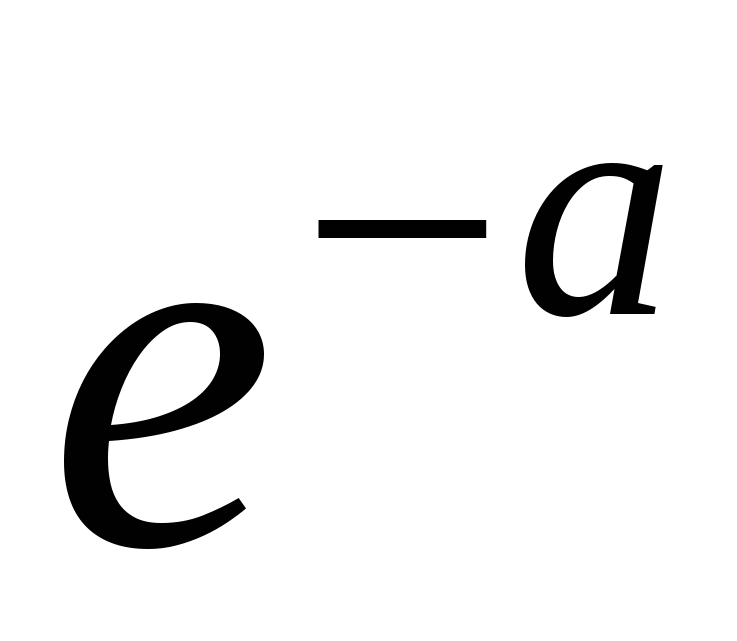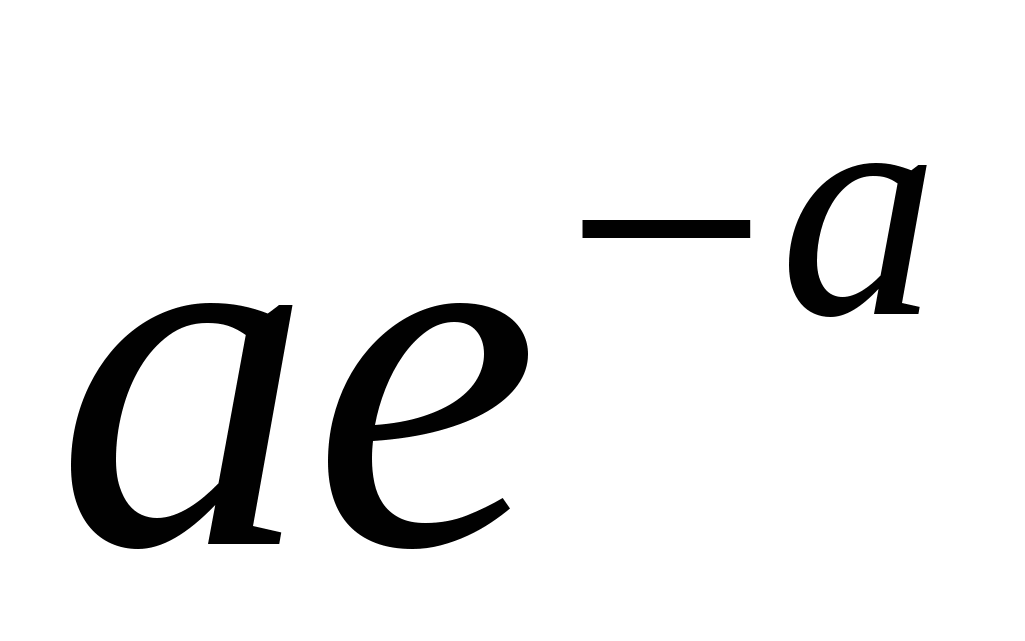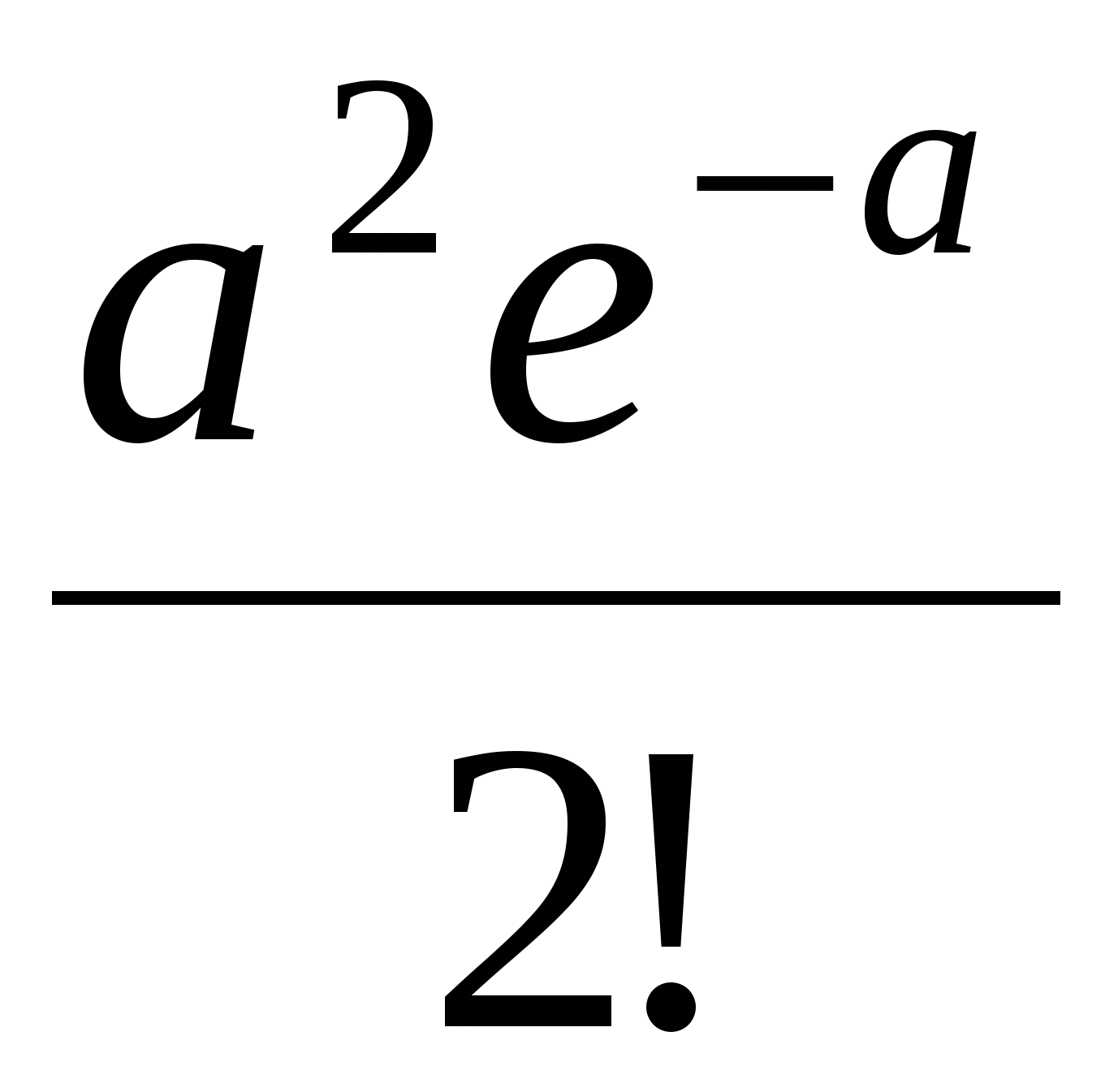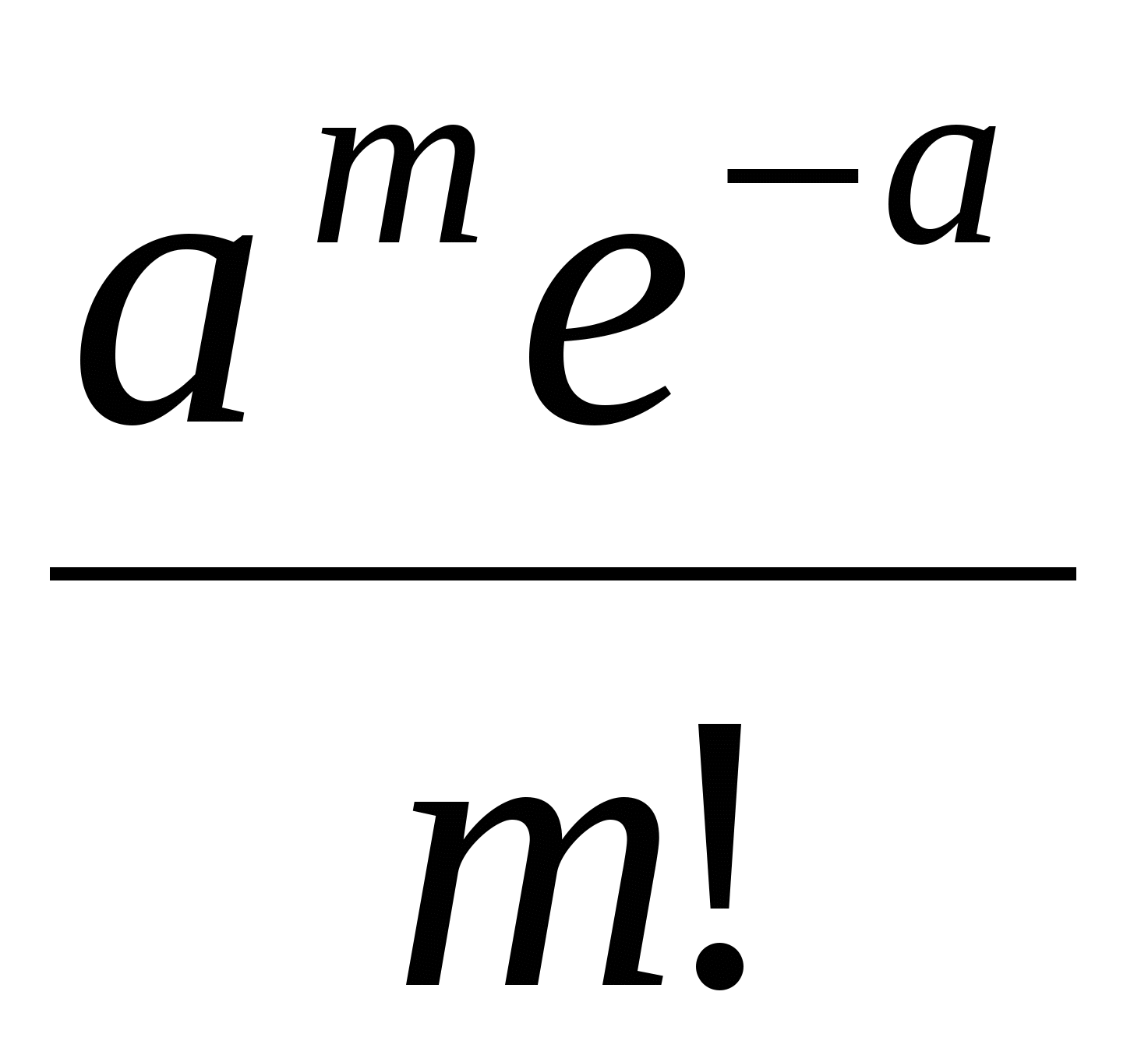Свойства закона распределения Пуассона.

Свойство 1. Сумма вероятностей всех возможных значений пуассоновской случайной величины равна единице, т.е.

.

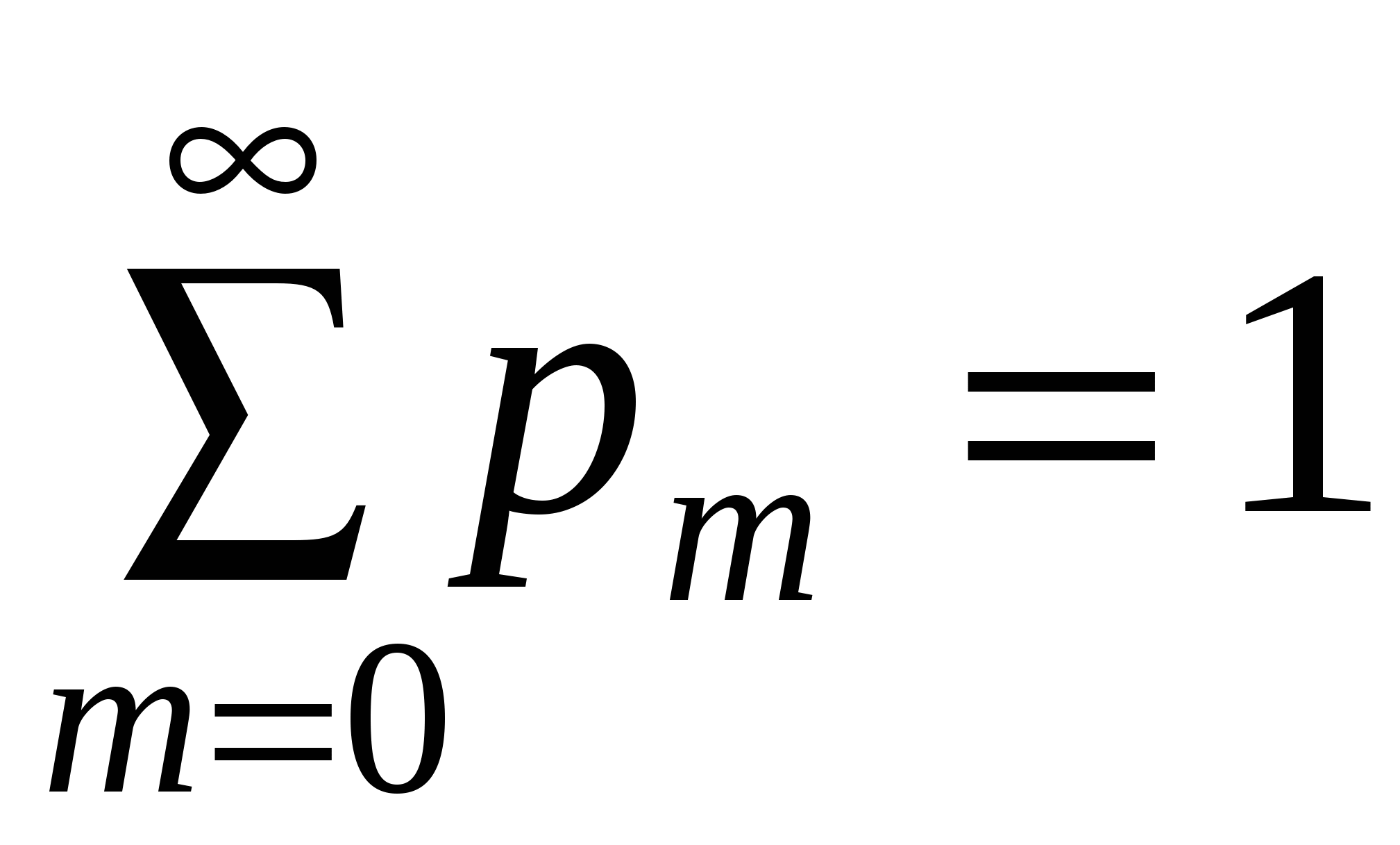Доказательство.Найдем сумму ряда

.●

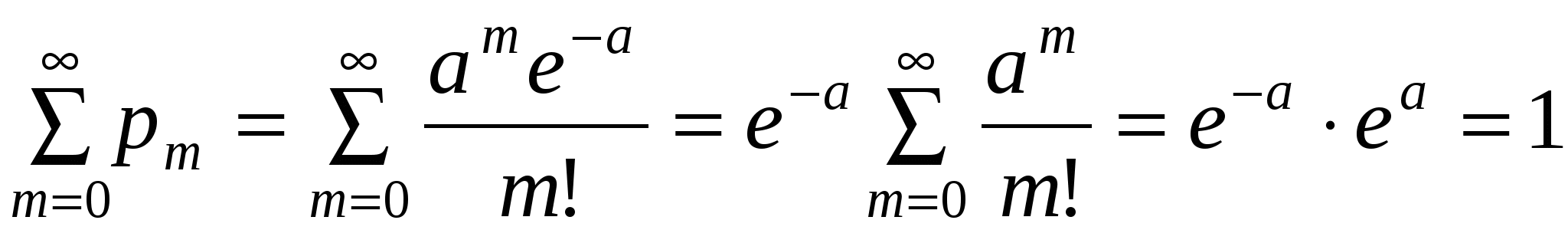Установим теперь теоретико-вероятностный смысл параметра закона распределения Пуассона.

Свойство 2. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, равны между собой, причем имеют место равенства

.

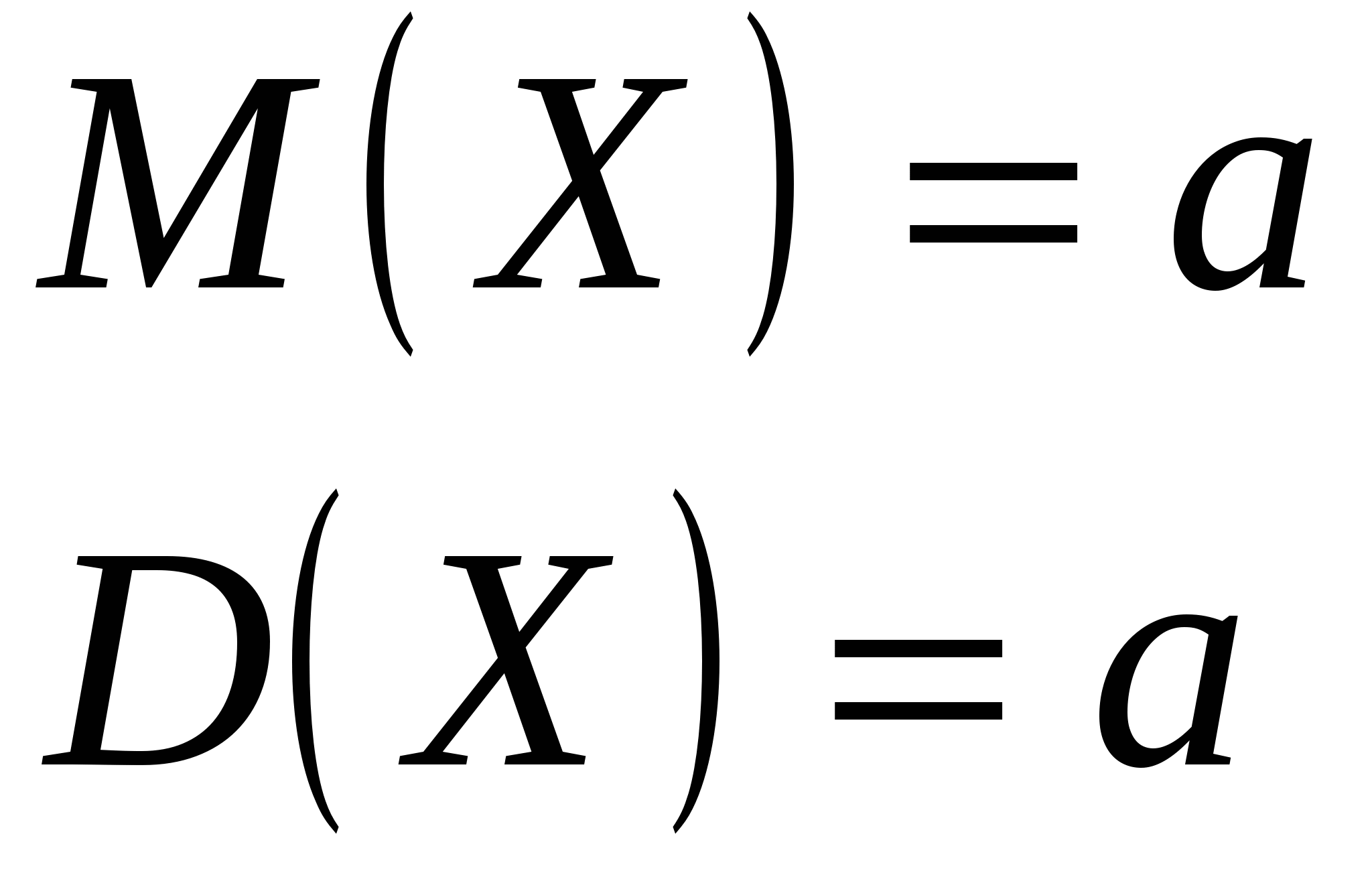Доказательство.Пользуясь определением математического ожидания, находим математическое ожидание пуассоновской случайной величины, заданной таблицей 2.

.

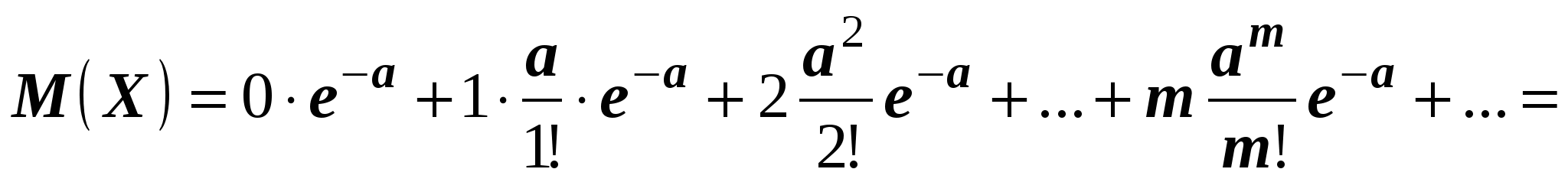
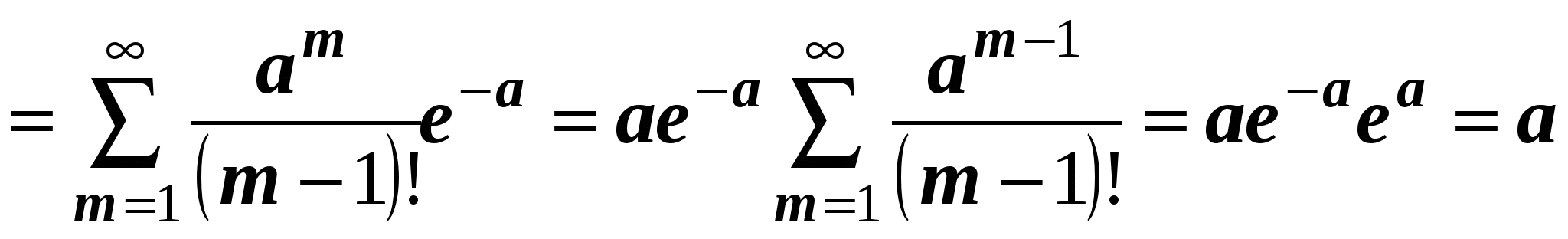Итак, доказано, что

.

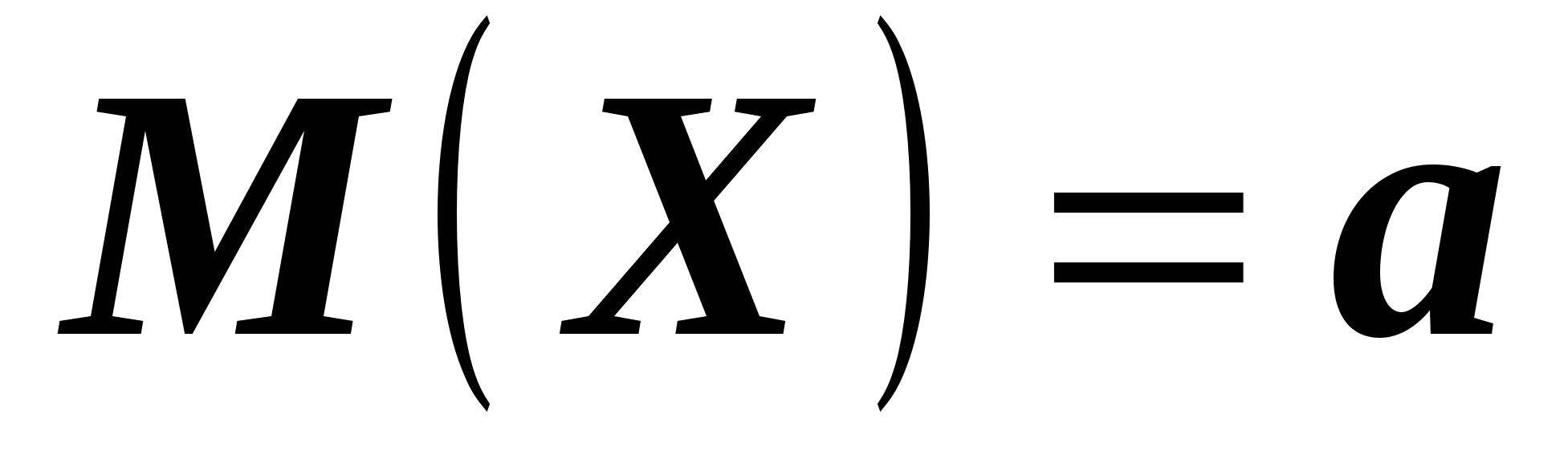Найдем теперь дисперсию пуассоновской случайной величины

.

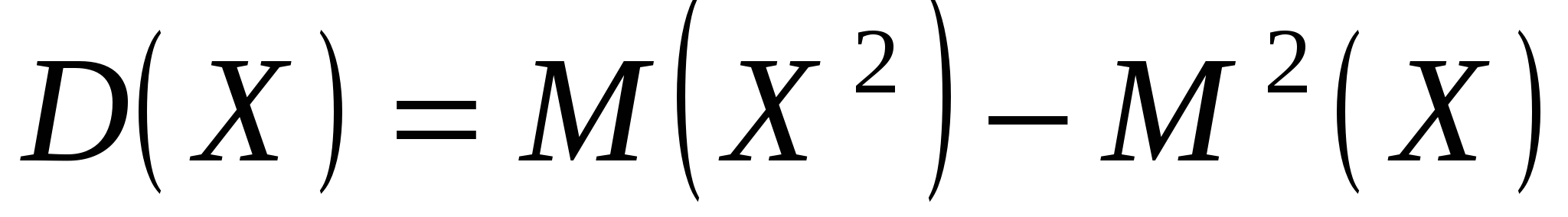Вычислим 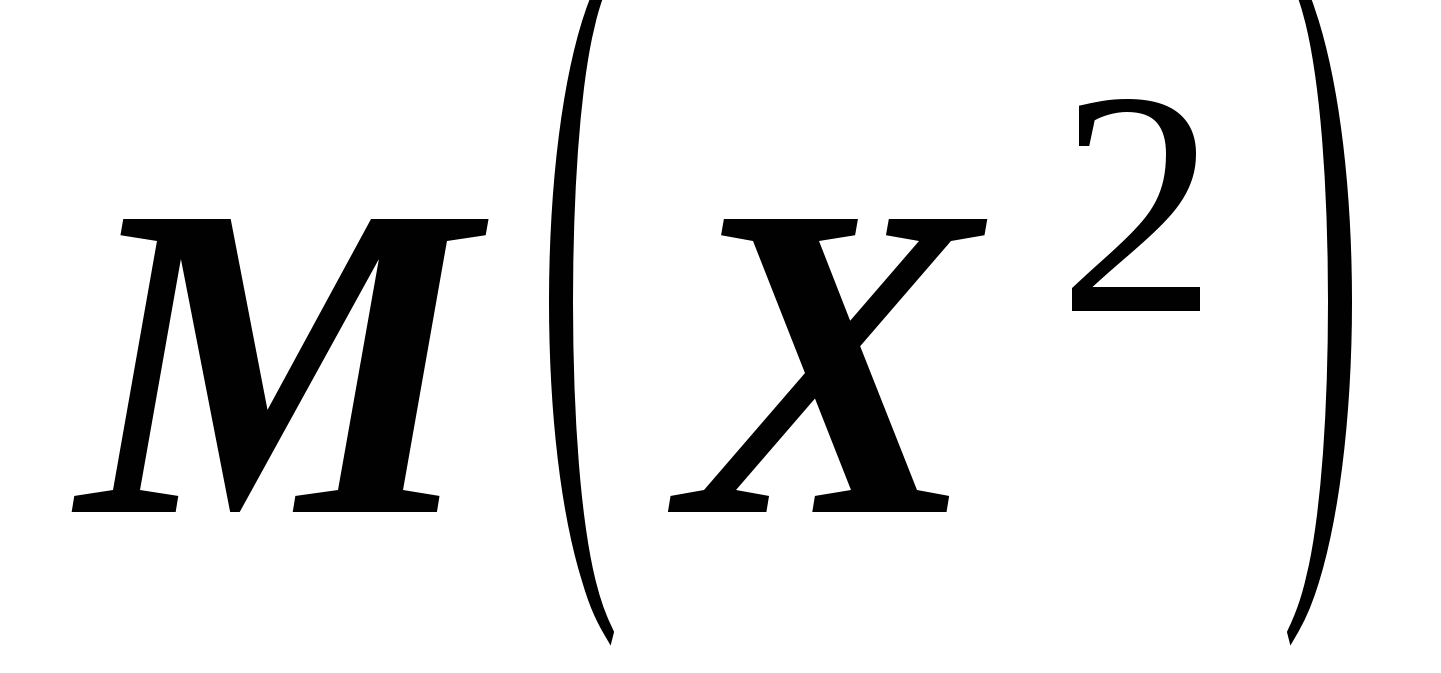, получим

.

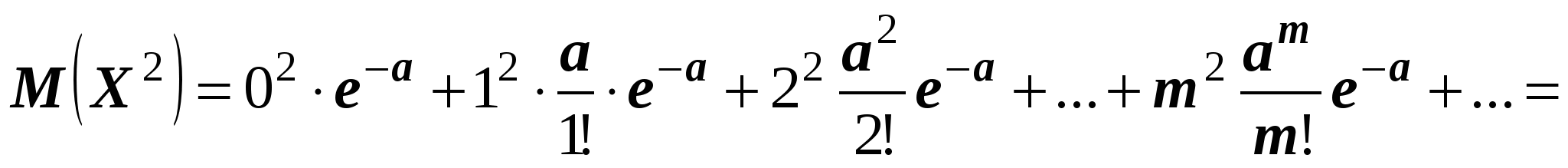
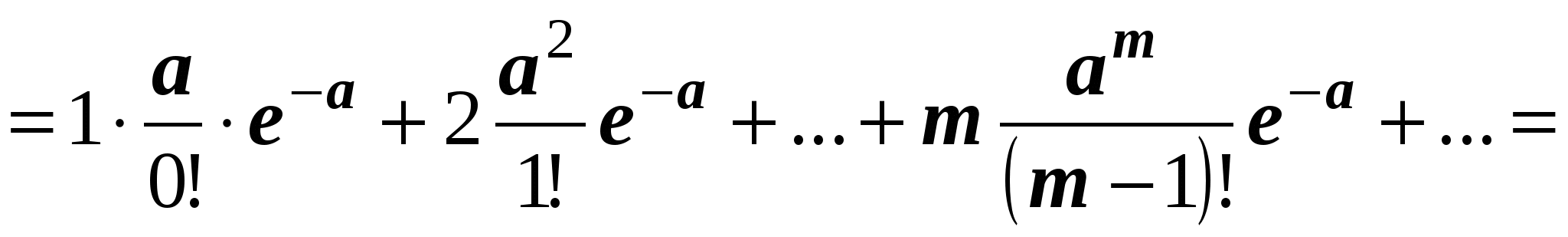
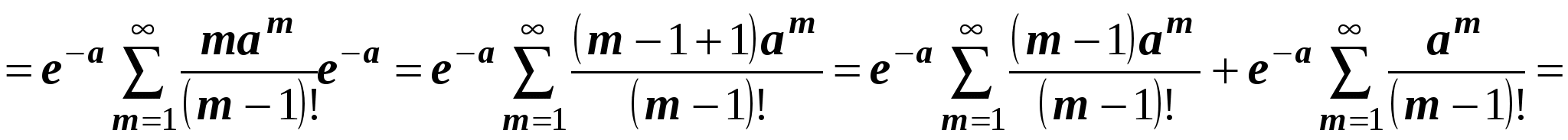
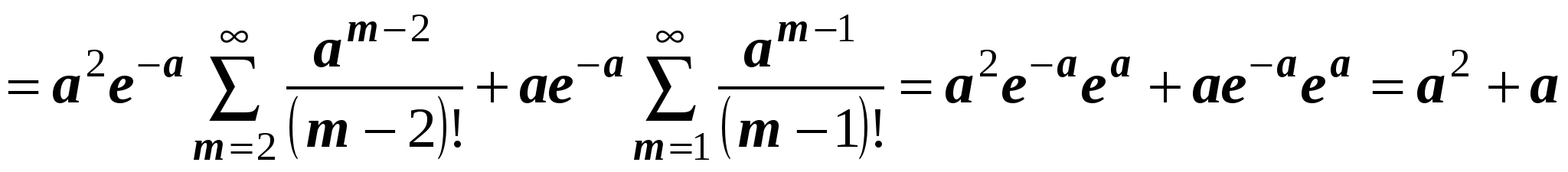Поэтому

. ●

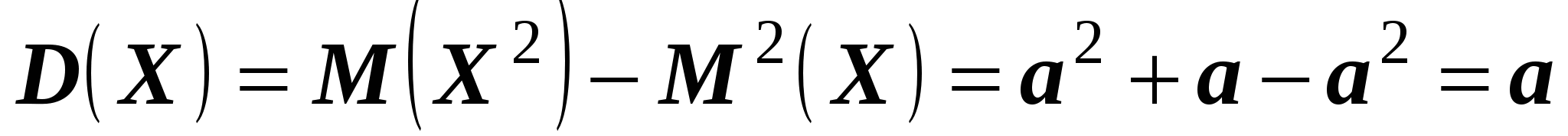Равномерное распределение

Определение. Непрерывная случайная величина называетсяравномерно распределеннойна отрезке 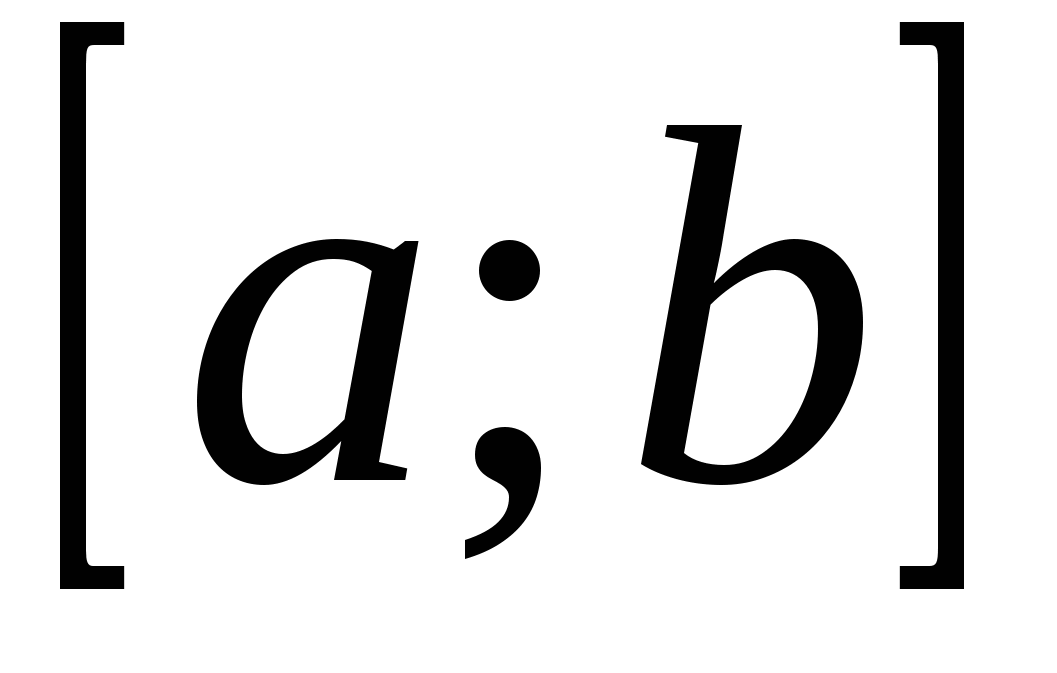, если все ее возможные значения содержатся на этом отрезке и плотность распределения вероятности постоянна.

Из определения следует, что дифференциальная функция равномерно распределенной случайной величины имеет вид

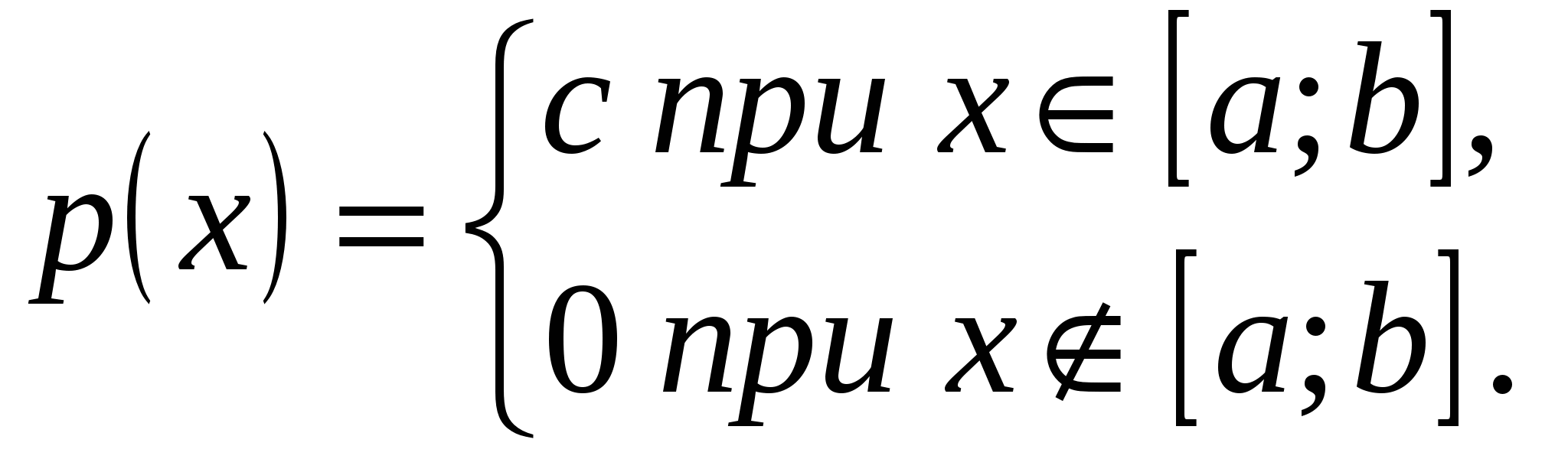
Свойства равномерного распределения

Свойство 1.Дифференциальная функция равномерно распределенной на отрезке случайной величины записывается в виде

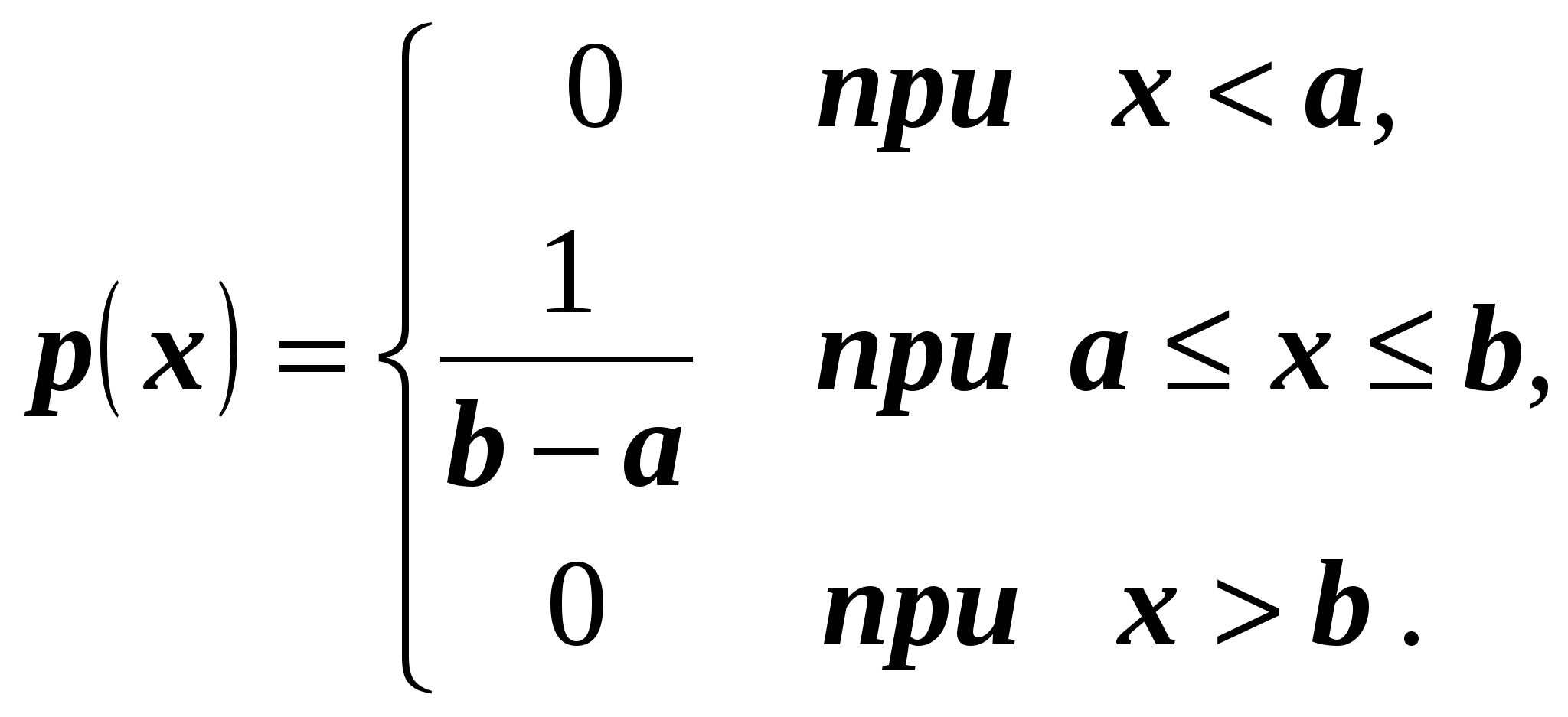(1)

Доказательство.

График плотности вероятности 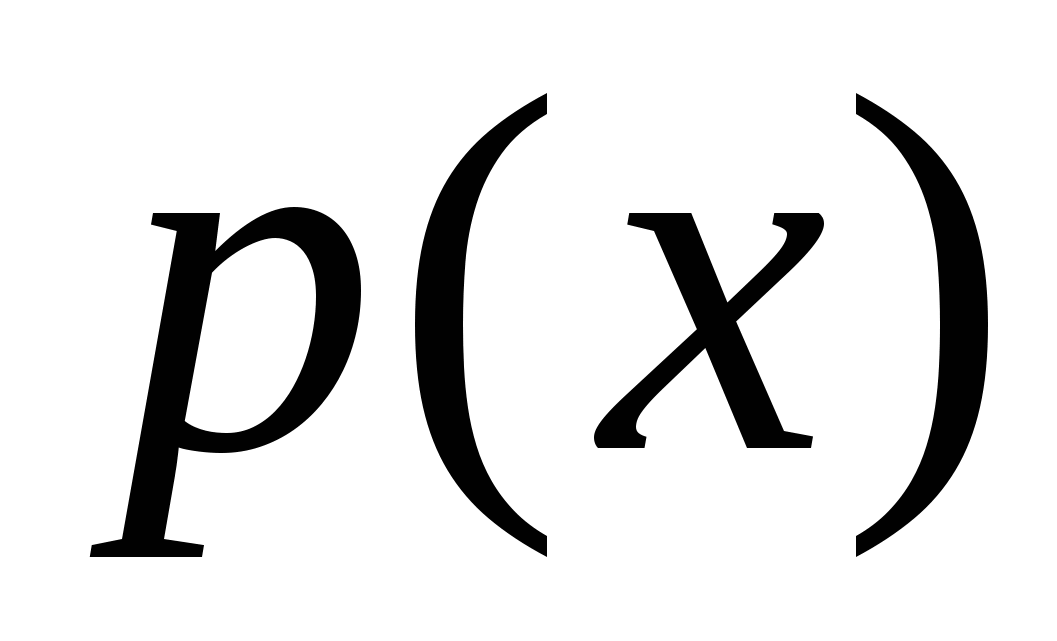равномерно распределенной случайной величины изображен на рисунке 1

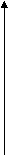
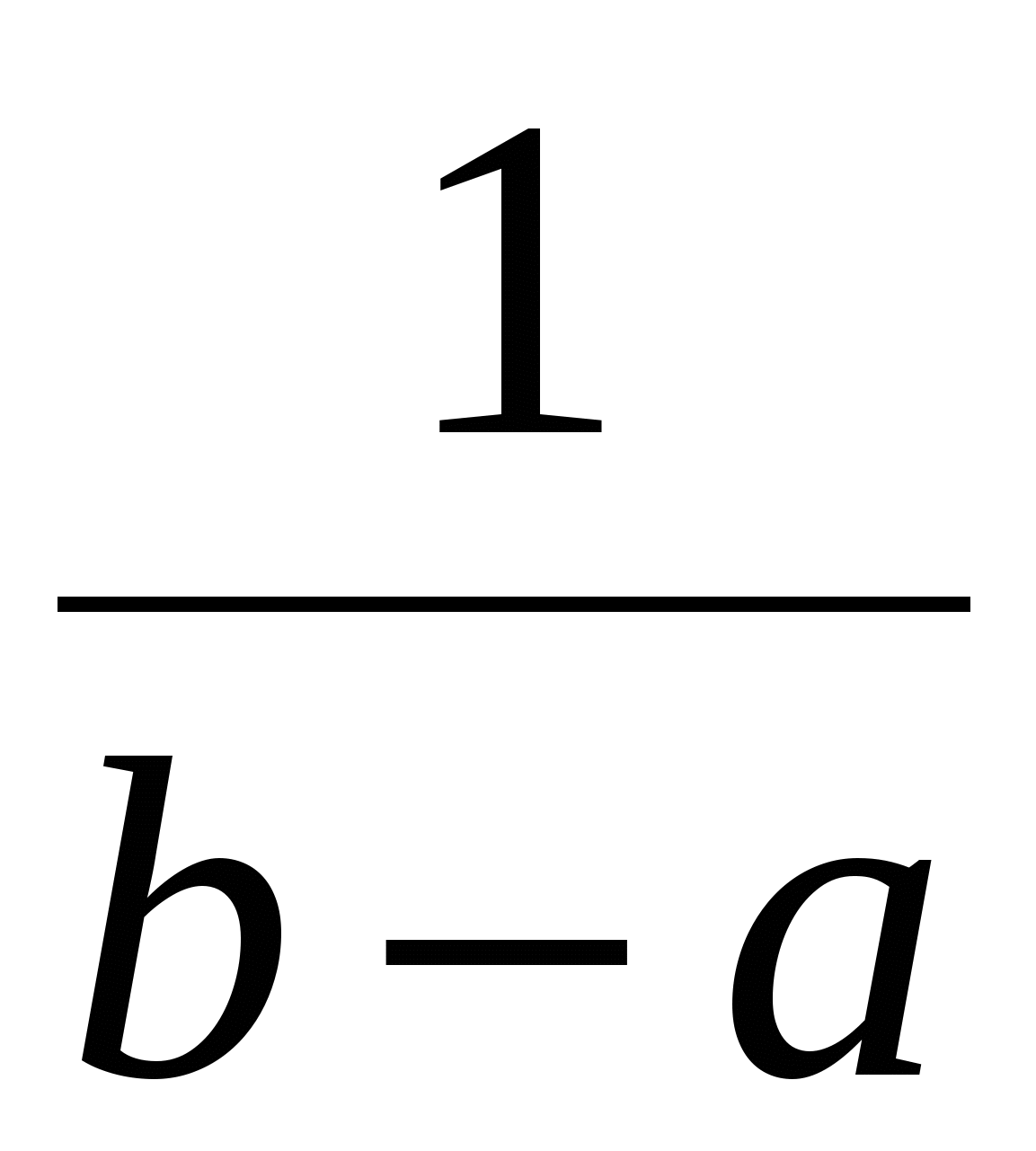
Рис. 1.

Свойство 2.Интегральная функция распределения случайной величины, равномерно распределенной на отрезке , записывается в виде

.

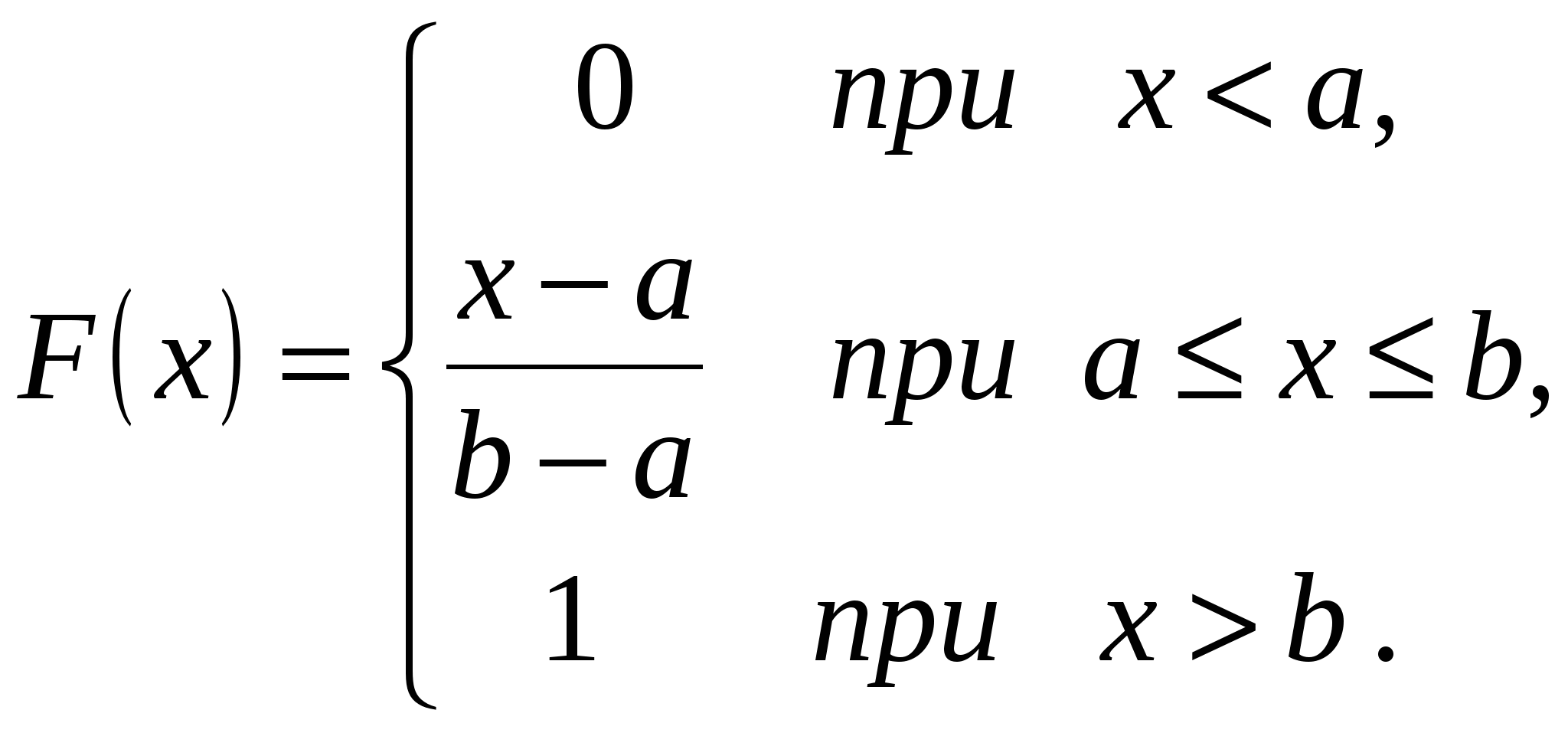Доказательство.

График интегральной функции равномерно распределенной случайной

величины изображен на рисунке 2.

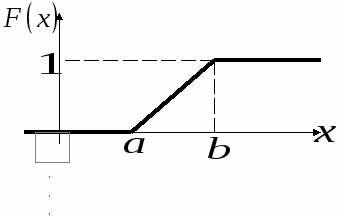Рис. 2.

Свойство 3. Математическое ожидание случайной величины, равномерно распределенной на отрезке , определяется по формуле

.

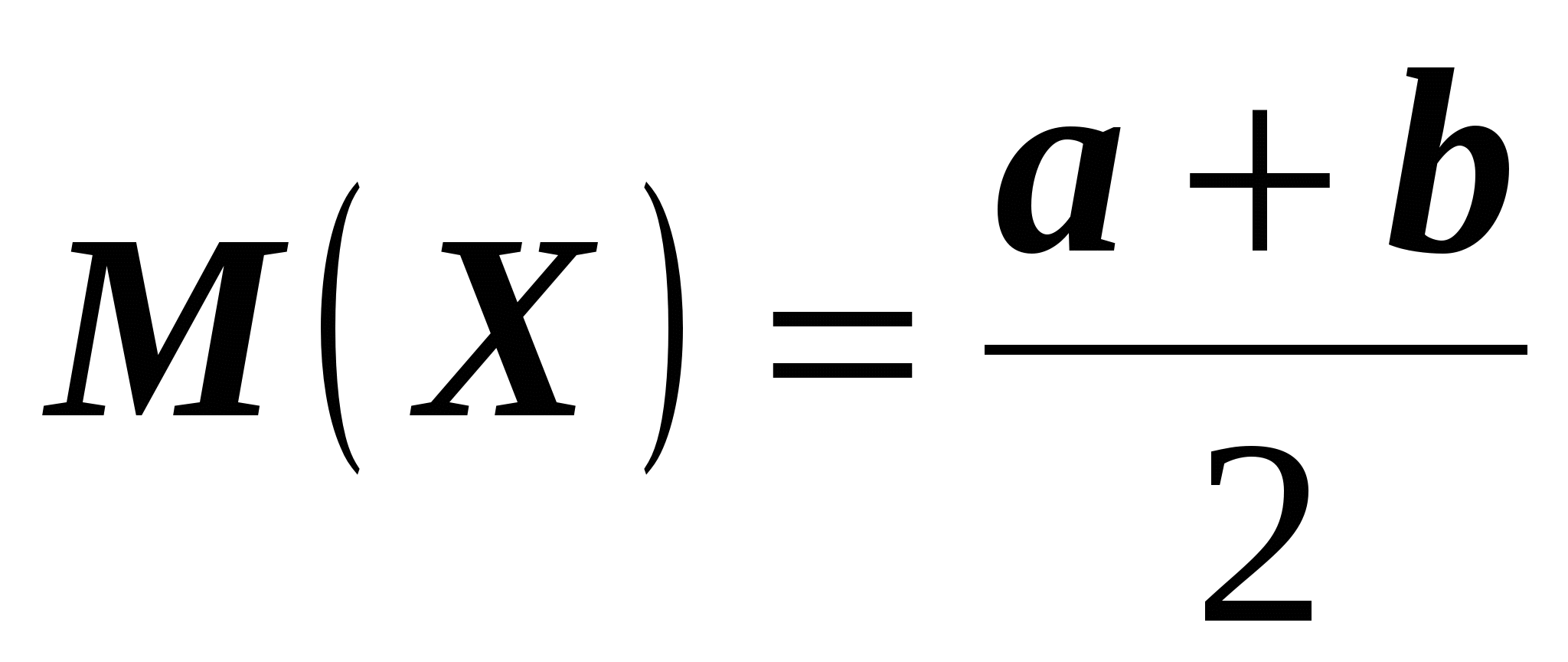Доказательство.

Свойство 4. Дисперсия случайной величины, равномерно распределенной на отрезке , определяется по формуле

.

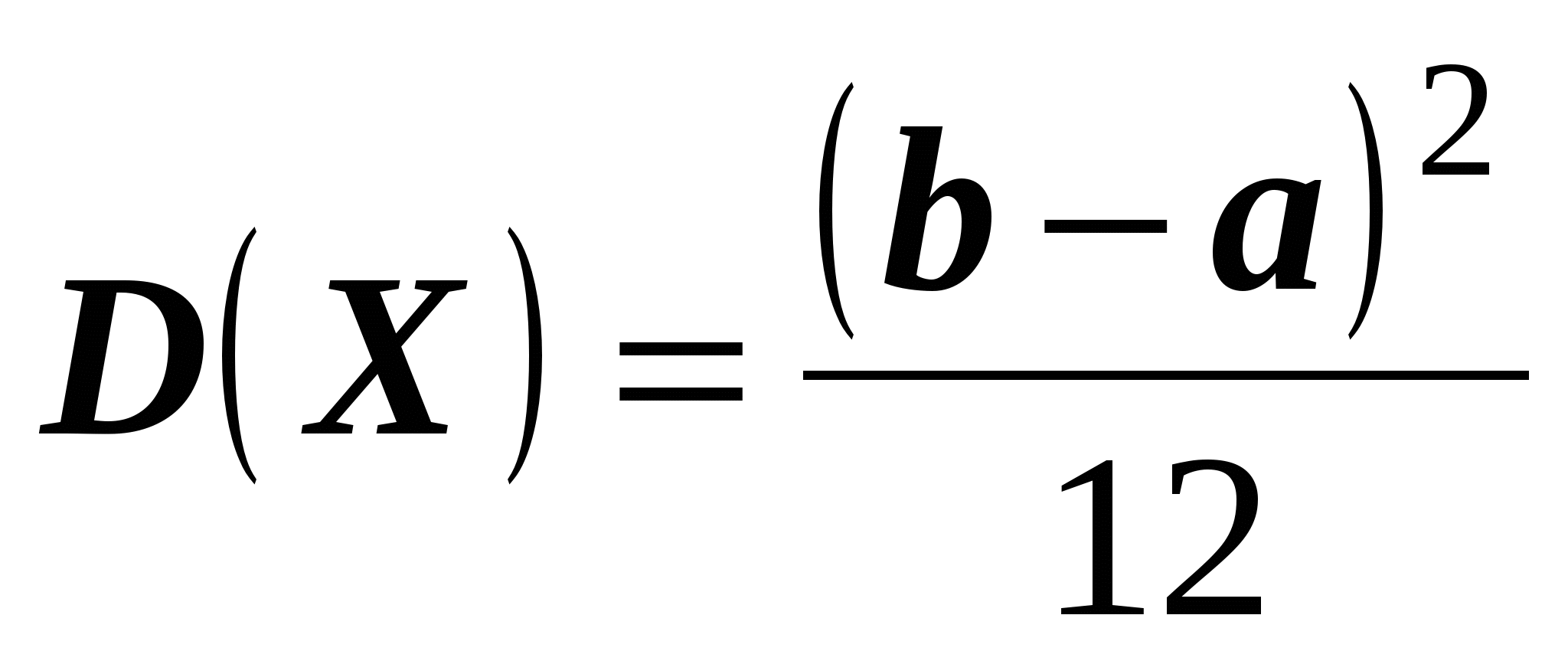Доказательство.

Свойство 5.Среднее квадратическое отклонение случайной величины равномерно распределенной на отрезке , вычисляется по формуле