Властивості криволінійного інтегралу ІІ роду

Криволінійний інтеграл визначається підінтегральним виразом, формою кривої інтегрування та напрямком інтегрування.

Властивість 1. При зміні напрямку інтегрування криволінійний інтеграл змінює знак.

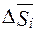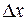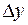Це виходить з означення, оскільки при цьому вектор , а відповідно і його проекції та змінюють знак.

Властивість 2. Розіб'ємо дугу інтегрування L на частини, нехай 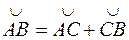. Тоді .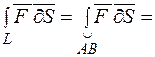

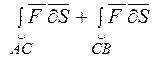Ця властивість справедлива для довільного числа доданків.

Теорема. Нехай у всіх точках деякої області D
функції P(x,y) та Q(x,y) разом зі своїми частинними
похідними 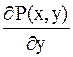та 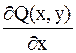неперервні. Тоді для того,
щоб криволінійний інтеграл по довільному замкненому
контуру L, який цілком лежить в області D, дорівнював нулю, тобто 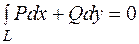, необхідно і достатньо
виконання умови 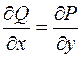у всіх точках області D.

Доведення. Нехай контур L обмежує область D.
Запишемо формулу Гріна: .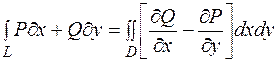

Якщо умова теореми виконана, то подвійний інтеграл
у правій частині дорівнює нулю і цим доведено достатність.

Доведемо необхідність. Допустимо, що ,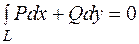
а умова не виконується, тобто 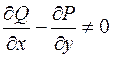хоча б в одній точці області D, скажімо, в точці P(x₀;y₀) .

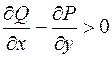Оскільки в лівій частині нерівності функція неперервна,
то вона буде додатня і у всіх точках деякої досить малої області D₁, яка містить в собі точку P(x₀,y₀). Візьмемо подвійний інтеграл по цій області, який матиме додатне значення: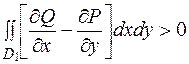

Але за формулою Гріна ліва частина нерівності дорівнює криволінійному інтегралу по контуру L₁, який обмежує область D₁, і дорівнює нулю. Виходить, наше допущення невірне і це приводить до висновку, що 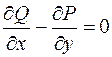в усіх точках області D.

Коли згадати, що рівність 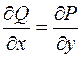є необхідною і достатньою умовою того, щоб вираз P(x,y)dx+Q(x,y)dy був повним диференціалом, то доведену теорему можна сформулювати таким чином: для того, щоб криволінійний інтеграл 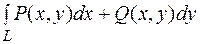не залежав від лінії інтегрування, необхідно і достатньо, щоб його підінтегральний вираз був повним диференціалом.

Підсумовуючи висновки нашого дослідження, можна стверджувати, що коли область D однозв'язна і функції P(x,y)
та Q(x,y) разом зі своїми частинними похідними в цій області неперервні, то всі чотири наступні твердження рівносильні, тобто якщо виконується одне з них, то виконуються і всі інші:

1). криволінійний інтеграл 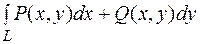, взятий по довільному замкненому контуру, цілком розміщеному в області D, дорівнює нулю;

2). криволінійний інтеграл 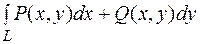не залежить від лінії інтегрування;

3). вираз 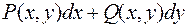є повний диференціал;

у всіх точках області D має місце рівність .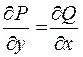

История інтеграла первого рода

Задача спрямления оказалась гораздо сложнее, чем вычисление площади, и в античные времена единственное успешное спрямление было выполнено для окружности. Декарт даже высказывал мнение, что «отношение между прямым и кривым неизвестно, и даже, думаю, не может быть познано людьми».

Первым достижением стало спрямление параболы Нейла (1657), выполненное Ферма и самим Нейлом. Вскоре была найдена длина аркициклоиды (Рен, Гюйгенс). Джеймс Грегори (ещё до открытия математического анализа) создал общую теорию нахождения длины дуги, которая немедленно была использована для различных кривых.

Джеймс Гре́гори (англ. James Gregory, ноябрь 1638, Драмоук, Абердиншир — октябрь 1675,Эдинбург) — шотландский математик и астроном. Наряду с Валлисом и Барроу — один из основоположников математического анализа, предшественник Ньютона, который высоко ценил Грегори и называл его в числе своих учителей и вдохновителей.

Интерес к математике, возможно, проявился у него под влиянием дяди, ученика Виета.

В 1664 году Грегори приехал в Лондон, познакомился с Гуком, Джоном Коллинзом и другими видными учёными. В 1664—1668 гг. совершил путешествие в Италию, попутно расширяя свой математический кругозор. Там он ознакомился, в частности, с методом неделимых Кавальери и начал собственные исследования в области применения бесконечно малых.

Важнейшие математические работы Грегори начинаются в 1667 году. Он подготовил статью по математическому анализу, которую послал Гюйгенсу. Тот не ответил, но опубликовал в своём журнале обзор статьи, где часть результатов объявил ошибочными, а относительно верных результатов объявил, что он открыл их раньше, чем Грегори. В дальнейшем Грегори воздерживался от публикации части наиболее выдающихся своих достижений, и они были обнаружены только после его смерти.

Декарт использовал инфинитезимальные методы в своей «Оптике», но в целом старался не углубляться в эту область. В трактате «Геометрия» он высказал мнение, что спрямление алгебраических линий невозможно. Это утверждение было опровергнуто лишь через двадцать лет: в 1650-х гг. сразу четыре математика, включая Ферма и Гюйгенса, дали спрямление полукубической параболы. Впрочем, и сам Декарт успешно спрямил, правда, не алгебраическую, а трансцендентную кривую — логарифмическую спираль, длина дуги которой, считая от полюса, пропорциональна радиус-вектору конца дуги — свойство, которое знал и Торричелли.

Идея Валлиса — алгебраизация метода бесконечно малых — достигла высшего развития после открытия математического анализа Ньютономи Лейбницем. В своих «Началах» Ньютон дал первый набросок общей теории пределов (11 лемм), при этом он не постулирует аналог принципа Кавальери, а строго его доказывает (следствие из леммы IV):

Гюйгенс, Хёйгенс (Huygens) Христиан (14. 4. 1629, Гаага, — 8. 7. 1695, там же), нидерландский механик, физик и математик, создатель волновой теории света. Первый иностранный член Лондонского королевского общества (с 1663). Г. учился в университетах Лейдена и Бреды, где изучал юридические науки и математику. В 22 года он опубликовал работу об определении длины дуг окружности, эллипса и гиперболы. В 1654 появилась его работа "Об определении величины окружности", явившаяся важнейшим вкладом в теорию определения отношения окружности к диаметру (вычисление числа p). Затем последовали другие значительные математические трактаты по исследованию циклоиды, логарифмической и цепной линии и др. Его трактат "О расчётах при игре в кости" (1657) — одно из первых исследований в области теории вероятностей. Г. совместно с Р. Гуком установил постоянные точки термометра — точку таяния льда и точку кипения воды. В эти же годы Г. работает над усовершенствованием объективов астрономических труб, стремясь увеличить их светосилу и устранить хроматическую аберрацию. С их помощью Г. открыл в 1655 спутник планеты Сатурн (Титан), определил период его обращения и установил, что Сатурн окружен тонким кольцом, нигде к нему не прилегающим и наклонным к эклиптике. Все наблюдения приведены Г. в классической работе "Система Сатурна" (1659). В этой же работе Г. дал первое описание туманности в созвездии Ориона и сообщил о полосах на поверхностях Юпитера и Марса.

Уже Архимед в своих исследованиях рассекал пространственное тело параллельными плоскостями и представлял это тело как своего рода альбом, объединение таких сечений (инфинитезимальное разложение, то есть разложение на бесконечно малые элементы). Здесь возможно влияние атомистов с их «неделимыми». Однако Архимед считал обязательным передоказывать результаты, полученные с помощью метода неделимых, строгим методом исчерпывания. Европейские математики, начиная с XVI века, тоже применяли метод исчерпывания для проведения квадратур (вычисления площадей) и определения центров тяжести.

В XVII веке сразу несколько математиков реализуют идею инфинитезимального разложения плоской фигуры или трёхмерного тела. Среди нихНепер, Кеплер, Декарт, Ферма, Кавальери и др. Строго обосновать новый метод они не могли, ссылаясь на то, что результаты получаются правильные, и при желании эти результаты можно доказать громоздким классическим методом. В большинстве случаев это было верно, однако не всегда — например, при вычислении площади неограниченной фигуры метод исчерпывания был неприменим, а новый метод нередко давал верный результат. Классический подход не работал также при суммировании многих рядов и в других случаях работы с бесконечностью.

В труде «Новая астрономия» Кеплер часто использует понятие «неделимых», в том числе при формулировке своих трёх законов движения планет; например, вместо площади он упоминал «сумму радиус-векторов». В «Новой стереометрии винных бочек» он находит объём множества тел, полученных вращением конических сечений; для вычисления объёма Кеплер разлагает тело в набор сечений и затем собирает этот набор в ином теле, объём которого известен. Большинство его результатов были правильны, хотя несколько ошибок Кеплер всё же допустил^[2].

Галилей был знаком с методом неделимых, однако отчётливо видел его слабые и опасные стороны. В переписке и последних трудах он размышляет о сущности бесконечности, показывает, что бесконечное множество может быть равносчётно своей части, имеющей меньшую меру, так что рассуждения о неделимых плохо обоснованы. Тем не менее он сам фактически использовал неделимые при исследованииравноускоренного движения^[2].

Наиболее ярким и влиятельным представителем «геометрии неделимых» был Кавальери. В его изложении инфинитезимальные представления Кеплера обрели вид общих вычислительных приёмов.

Мощь и относительная простота нового метода произвели чрезвычайно сильное впечатление на математиков. Целые поколения, от Валлиса доЛейбница, учились у Кавальери. Торричелли назвал метод неделимых «царской дорогой» в геометрии.

Валлис, ознакомившись с методом Кавальери по книге Торричелли, решил провести его алгебраизацию. Вместо геометрического преобразования сечений он строит в «Арифметике бесконечных» (1656) числовые ряды, которые мы сейчас называем интегральными суммами, и находит эти суммы.

Независимо от Валлиса и лет на 30 раньше эти интегралы вычислили Ферма и Роберваль. В посмертно опубликованном сочинении Ферма виртуозно применяет такие приёмы, как интегрирование по частям и замена переменных, что позволило ему вычислить множество сложных интегралов от дробно-рациональных функций и от многочленов с дробными степенями.

Мемуар Ферма получил широкую известность, так как он почти полностью покрывает результаты Кавальери, но при этом изложенные методы существенно компактнее и понятнее. Кроме того, интегральные суммы оказались применимы к задачам, недоступным для метода Кавальери — например, спрямление (измерение дуги) кривой. Роберваль исследовал спираль Архимеда, Ферма и Торричелли в 1640-е годы —параболы и спирали высших порядков. Кристофер Рен спрямил циклоиду (1658).

Учитывая уязвимость для критики тех открытий, которые получены с помощью метода неделимых, многие математики (Ферма, Паскаль,Барроу и др.) отмечали в своих работах, что все их результаты могут быть без труда передоказаны строгими методами древних. Барроу, правда, сделал к этой оговорке ироничное добавление: «только зачем?».^[3]

Декарт использовал инфинитезимальные методы в своей «Оптике», но в целом старался не углубляться в эту область. В трактате «Геометрия» он высказал мнение, что спрямление алгебраических линий невозможно. Это утверждение было опровергнуто лишь через двадцать лет: в 1650-х гг. сразу четыре математика, включая Ферма и Гюйгенса, дали спрямление полукубической параболы. Впрочем, и сам Декарт успешно спрямил, правда, не алгебраическую, а трансцендентную кривую — логарифмическую спираль, длина дуги которой, считая от полюса, пропорциональна радиус-вектору конца дуги — свойство, которое знал и Торричелли.

Идея Валлиса — алгебраизация метода бесконечно малых — достигла высшего развития после открытия математического анализа Ньютономи Лейбницем. В своих «Началах» Ньютон дал первый набросок общей теории пределов (11 лемм), при этом он не постулирует аналог принципа Кавальери, а строго его доказывает (следствие из леммы IV):

Клеро, Алекси Клод (франц. Clairaut, Аlеxis Сlаude, 7 мая 1713, Париж, - 17 мая 1765, там же) – французский математик, геометр и астроном, иностранный почётный чл.Петербургской АН (1754), чл. Парижской АН (1731). В математическом анализе ввёл понятия криволинейного интеграла (1743), полного дифференциала, функции нескольких независимых переменных (1741), а также общего и особого решения дифференциальных уравнений 1-го порядка (1736). Разработал. новую теорию движения Луны (1751), провёл исследования фигуры 3ёмли, доказав ряд фундаментальных для высшей геодезии теорем. На основе изучения движения кометы Галлея в 1759 определил момент её предстоящего прохождения через перигелий (погрешность была только ок. 1 мес). В механике создал динамическую теорию относительного движения.

Уже в двенадцать лет читал в парижской академии наук свой доклад о новых кривых, а в 18 лет был избран академиком. Как астроном, Клеро, кроме новой теории Луны, получившей премию Санкт-петербургской академии наук, известен вычислением орбиты периодической кометы Галлея. Её появление 1759 он назначил вперед с ошибкой менее месяца; по времени это было первое предвычисление кометной орбиты, в котором приняты в расчет возмущающие действия планет. В геодезии, кроме личного участия в градусном измерении в Лапландии (1736—1787), Клеро определил соотношение между силой тяжести и сжатием Земли, известного под названием теоремы Клеро и давшего возможность определять сжатие Земли независимо от градусных измерений, из наблюдений над качаниями маятника в разных местах земной поверхности. Главные сочинения Клеро: «Théorie de la figure de la Terre», «Théorie de la Lune» «Tables de la Lune» и «Théorie du mouvement des comètes».

Алексис Клод Клеро (французское имя - Alexis Claude Clairaut)
французский математик и астроном, иностранный почётный член Санкт-Петербургской Академии Наук (1754), член Парижской Академии (1731). Клеро родился в Париже, в семье преподавателя математики. Его отец Жан Батист Клеро был профессором математики в Париже и корреспондентом Академии Наук в Берлине. Уже в возрасте двенадцати лет он поразил парижских академиков своей работой о некоторых кривых четвёртого порядка, и они устроили Клеро целый экзамен, чтобы убедиться в его авторстве. Экзамен Клеро выдержал. В 1729 году 16-летний Клеро представил той же академии новый трактат: «Исследования о кривых двоякой кривизны». Эта книга положила начало сразу трём геометрическим дисциплинам: аналитической геометрии в пространстве (Декарт занимался плоскими кривыми), дифференциальной геометрии и начертательной геометрии. Шефство над юным дарованием взял Пьер Луи де Мопертюи, который отвёз Клеро в Базель слушать лекции Иоганна Бернулли. По возвращении (1731) восемнадцатилетний Клеро был избран членом (адъюнктом) Парижской академии — беспрецедентный случай в истории Академии. Спустя несколько лет Академия решила положить конец долгим спорам о том, сплющена ли наша планета (как доказывал Ньютон) или, наоборот, вытянута у полюсов наподобие лимона. Для проведения измерений длины градуса меридиана были организованы экспедиции (1735—1737 годы) в Перу и Лапландию. Клеро принял участие в лапландской экспедиции (1736), вместе с Мопертюи. Измерения подтвердили точку зрения Ньютона: Земля сжата у полюсов, коэффициент сжатия, по современным данным, равен 1/298,25 (Ньютон предсказывал 1/230). В 1741 году была организована ещё одна экспедиция с той же целью, и тоже с участием Клеро. По возвращении Клеро написал классическую монографию «Теория фигуры Земли, извлечённая из принципов гидростатики» (1743). Эйлер писал об этой работе: «Книга Клеро есть произведение несравненное как в отношении глубоких и трудных вопросов, которые в ней рассматриваются, так и в отношении того удобного и лёгкого способа, посредством которого ему удаётся совершенно ясно и отчётливо изложить предметы самые возвышенные».
Клеро неожиданно скончался в Париже 17 мая 1765 года. В математическом анализе Клеро ввёл понятия криволинейного интеграла (1743), полного дифференциала, а также общего и особого решения дифференциальных уравнений 1-го порядка (1736). Нельзя не отметить также, что Клеро подготовил блестящие учебники «Начала геометрии» и «Начала алгебры». Огромны заслуги Клеро в механике и особенно в утверждении системы Ньютона, которая даже в середине XVIII века всё ещё находила на континенте Европы немало противников. Основные трудности модель Ньютона встречала в теории движения Луны. Расхождения («неравенства») между видимым движением лунного апогея и вычисленным по закону всемирного тяготения оказывались столь значительными, что многие ученые, даже такие, как Эйлер, Даламбер и сам Клеро, высказывали сомнения в точности этого закона. По предложению Эйлера Санкт-Петербургская академия наук объявила в 1749 году свой первый научный конкурс на следующую тему: «Согласуются или же нет все неравенства, наблюдаемые в движении Луны, с теорией Ньютона? И какова истинная теория всех этих неравенств, которая позволила бы точно определить местоположение Луны для любого времени?» Как раз в это время Клеро нашёл остроумный способ приближённого решения «задачи трёх тел». Он уточнил свои прежние вычисления, и они с высокой точностью совпали с последними результатами наблюдений. На основании отзыва Эйлера, книга Клеро «Теория Луны, выведенная из единственного начала притяжения, обратно пропорционального квадратам расстояний», была заслуженно удостоена премии (1751). Вскоре небесную механику ожидал новый триумф. Уже Галлей понял, что кометы, наблюдавшиеся в 1607-м и 1682-м годах — это одна и та же комета, получившая имя Галлея. Следующее появление этой кометы ожидалось в начале 1758 года. Однако Клеро, проведя точные вычисления с учётом влияния Юпитера и Сатурна, предсказал (осенью 1758 года), что комета появится позднее и пройдёт перигелий в апреле 1759 года. Он ошибся всего на 31 день. Клеро доказал ряд фундаментальных для высшей геодезии теорем. Кроме упомянутого личного участия в градусном измерении в Лапландии (1736—1787), Клеро определил соотношение между силой тяжести и сжатием Земли, известного под названием «теоремы Клеро» и давшего возможность определять сжатие Земли независимо от градусных измерений, из наблюдений над качаниями маятника в разных местах земной поверхности. Тем самым были заложены основы нового направления науки — гравиметрии. В механике он создал динамическую теорию относительного движения. Клеро также далеко развил вслед за Ньютоном и Маклореном теорию фигур равновесия жидкой массы.Главные сочинения Клеро: «Thйorie de la figure de la Terre» (Теория формы Земли); «Thйorie de la Lune» (Теория движения Луны); «Tables de la Lune» (Таблицы движения Луны); «Thйorie du mouvement des comиtes» (Теория движения комет). Литература: Клеро А.К. Теория фигуры Земли, основанная на началах гидростатики. Серия: Классики науки. Москва-Ленинград : Издательство Академии Наук СССР, 1947; История математики под редакцией А.П.Юшкевича в трёх томах. Москва : Наука. Том 3: Математика XVIII столетия, 1972; Идельсон Н.И. Этюды по истории небесной механики. Москва : Наука, 1975; Клеро, Алекси Клод // Математический энциклопедический словарь. Главный редактор Ю.В.Прохоров. — Москва : «Большая Российская энциклопедия». — 1995; Brunet Р., La vie et l’oeuvre де Clairaut, Р., 1952.

http://books.google.com.ua/books?id=nIKVQCeI1FUC&pg=PA79&lpg=PA79&dq=history+of+mathematics+line+integral+Clairaut&source=bl&ots=Z9gG2ukPZ4&sig=s2JAUk5pG35BVohDwBuXiXN8z-w&hl=ru#v=onepage&q=history%20of%20mathematics%20line%20integral%20Clairaut&f=false