Ковариационная матрица двумерной непрерывной случайной величины,коэффициенткорреляции,пределызначений,доказательство;независимость и некоррелированность:понятие и признаки. 2 страница

2.2. Кондиционирование результатов экспериментов.Пусть случайная величина x непрерывна. В этом случае все выборочные значения будут различны. После получения выборочных значений случайной величины в хронологическом порядке первым шагом в их обработке является сортировка в порядке возрастания. Это действие осуществляется автоматически при расстановке выборочных значений на числовую ось. Порядковые номера выборочных значений изменяются, и новые порядковые номера указываются в скобках: 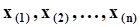.Выборка, отсортированная таким образом, называется вариационным рядом, отдельные элементы - членами вариационного ряда. Первый и последний члены называются крайними членами вариационного ряда. Если кол-во членов вариационного ряда нечетное, то существует единственный средний член вариационного ряда, номер которого (2n + 1)/2 . Средний член вариационного ряда наз-сявыборочной медианой.Следующий шаг - построение выборочной функции распределения 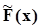, которая является оценкой генеральной функции распределения F(x). Пример выборочной функции распределения приведен на рис.

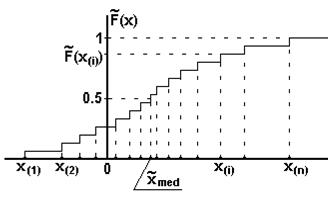Выборочная ф-я распределения изображается ступенчатой линией. Абсциссами каждого скачка этой линии являются выборочные значения 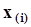. Высота всех ступеней одинакова и =1/n. При каждом значении 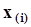ординатами каждой ступени являются значения выборочной функции распределения 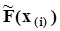. На множестве экспериментов, повторяющихся в неизменных условиях, выборочные значения являются случайными величинами, распределенными так же, как и генеральная совокупность, из которой они извлекаются, то есть F(x) - их функция распределения. А это значит, что реализуются условия упомянутого примера, из которого следует, что значения 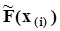, которые являются случайными на множестве повторяющихся экспериментов, распределены равномерно в интервале [0, 1]. Поэтому высота всех ступенек принята одинаковой.Оценкой плотности распределения является гистограмма. Гистограмма является выборочной плотностью распределения и в отличие от генеральной плотности распределения j(x)мы обозначим ее, как 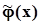. Пример гистограммы приведен на рис. Для построения гистограммы интервал между крайними членами вариационного ряда делится на M интервалов 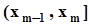равной длины D = 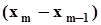. Подсчитывается кол-во 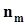выборочных значений, попавших в каждый m - ый интервал и вычисляется частость 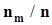, которая является оценкой вероятностной меры каждого интервала. Кол-во интервалов или их ширина выбирается таким образом, чтобы самый “бедный” интервал содержал 3 ¸ 5 выборочных значений. Далее на полученных интервалах, как на основаниях строятся прямоугольники, высота каждого из которых должна быть равна

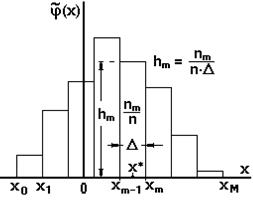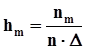. При таком построении площадь ги-мы будет =1, точно так же, как и под генеральной плотностью распределения, оценкой является гистограмма. 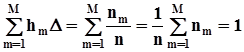. За счет группирования выборочных данных часть информации о случайной величине, теряется. Выборочная функция сохраняет всю информацию, содержащуюся в выборочных данных.

27.Точечное оценивание квантилей, интерквантильного промежутка, моментов и параметров плотности распределения по выборочной функции распределения, оценивание математического ожидания по гистограмме.2.3. Точечное оценивание.Точечной статистической оценкой называется оценка числовой характеристики или параметра генеральной совокупности, выражаемая одним числом.2.3.1. Оценивание квантилейОценивание квантилей выполняется по выборочной функции распределения, по сути дела, графическим способом. Это можно показать на примере точечного оценивания медианы, то есть 50%- ной квантили 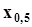. Для этого по заданной вероятности q = 0,5на графике выборочной функции распределения (рис. 26) проводится горизонтальная прямая до ее пересечения с выборочной функцией распределения. Абсцисса точки пересечения есть искомая оценка 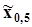, которая является выборочной медианой 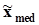. Этой абсциссой при нечетном n = (2k + 1) обязательно окажется, по построению, выборочное значение - средний член вариационного ряда 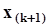.Для оценки других квантилей, например, квартили 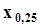или децили 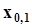горизонтальные линии проводятся на уровне вероятности 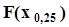= 0,25 или 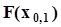= 0,1 соответственно. Так же находятся точечные оценки высоковероятных квантилей 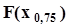или . 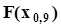Из графика рис. 26 видно, что абсциссой пересечения выборочной функции распределения с любой горизонтальной прямой обязательно окажется одно из выборочных значений. И здесь необходимо обратить внимание на следующее обстоятельство.

Пусть необходимо оценить квантиль 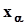при 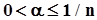или квантиль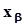 при 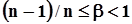. При задании вероятностей a и b из указанных промежутков оценками соответствующих квантилей неизменно окажутся первый или последний члены вариационного ряда независимо от заданных значений вероятностей, что будет свидетельствовать о крайне низкой достоверности этих оценок. Для того, чтобы не сталкиваться с подобной ситуацией, необходимо установить минимально допустимый объем выборки, обеспечивающий достаточную достоверность получаемых оценок квантилей в зависимости от задаваемой вероятности. Эту задачу мы решим, исходя из приведенных выше неравенств:

- в случае задания значения вероятности, не превышающего 0.5,

,

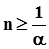- в случае задания значения вероятности, превышающего 0.5,

.

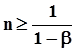Так, например, если задана вероятность a = 0.05 , то для точечного оценивания квантили 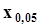объем выборки не должен быть меньше 20. Если задана вероятность b = 0.99 , то для точечного оценивания квантили 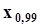объем выборки не должен быть меньше 100. Рекомендуется увеличивать объем выборки сверх минимального, указанного этими неравенствами, чтобы застраховаться от возможных грубых промахов измерений, которые могут быть вызваны импульсными помехами или сбоями аппаратуры.Точечное оценивание границ интерквантильного промежутка.Пусть стоит задача получить точечные оценки границ интерквантильного промежутка 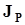. Как следует из п. 1.6.2, генеральными граничными квантилями этого промежутка являются 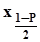и 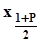. Поэтому точечное оценивание границ интерквантильного промежутка состоит в поочередном оценивании каждой из этих квантилей при соблюдении указанных выше соотношений и рекомендаций относительно необходимого объема выборки, то есть-для оценки нижней границы 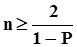,- для оценки верхней границы также 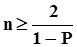.В частности, если заданоP = 0.95, то минимальный объем выборки составит 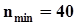.2.3.2. Точечное оценивание моментовОценке подлежат начальные моменты 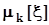и центральные моменты 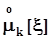случайной величины x , плотность распределения которой j(x). Основное внимание будет обращено на оценивание первых четырех моментов.

Статистические оценки генеральных моментов будем обозначать латинскими буквами и при необходимости показывать их зависимость от вектора выборочных значений 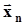.Соответствие между обозначениями генеральных моментов и их оценок представлено в таблице 1. Напомним, что в п. 2.1 было отмечено, что вектор выборочных значений является n - мерным случайным вектором на множестве групп экспериментов объемом n. Поэтому оценки моментов, вычисляемые по выборочным значениям, также случайны на том же множестве. Это означает, что оценки моментов,Таблица 1Обозначения генеральных моментов и их оценок

Генеральные моменты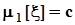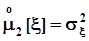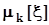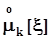
Оценки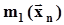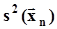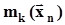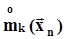

вычисленные по n выборочным значениям, будут различаться между собой случайным образом при повторении тех же n экспериментов в неизменных условиях, и, стало быть, являются случайными. Для них, как и для всех случайных величин, могут быть определены такие характеристики, как математическое ожидание, дисперсия, квантили и т.д.2.3.2.1. Оценивание моментов по выборочной функции распределенияДля получения оценок по выборочной функции распределения воспользуемся интегралом Стилтьеса (см., например, [4]).Интеграл Стилтьеса определен, как предел суммы Стилтьеса: 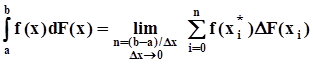,где f(x) и F(x) - две ограниченные функции, Dx - ширина участков, на которые разделен интервал [a, b], и если эти участки разной ширины, то тогда Dx - максимальная ширина, 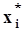- точка внутри i - го участка, 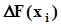- приращение функции F(x) на i - ом участке 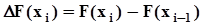.В случае, когда функция F(x) дифференцируема везде на[a, b], и ее производная есть 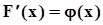, то интеграл Стилтьеса обращается в интеграл Римана: 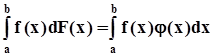.Если функция F(x)имеет ступенчатый характер, то есть в точках 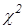она изменяется скачком,в остальных точк постоянна, то интеграл Стилтьеса вычисляется, как сумма ),

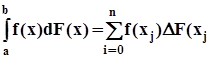где 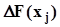- значение скачка функции F(x) в точках 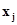.Применяя интеграл Стилтьеса для оценки начальных моментов по выборочной функции распределения, по определению моментов (п. 1.6.2), получим 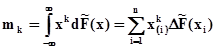.Но, как мы выяснили в п. 2.2, все скачки выборочной функции распределения в точках 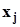одинаковы, равны 1/n,и их можно вынести за знак суммы. Кроме того, порядок перечисления слагаемых в сумме, стоящей справа, не имеет значения. Поэтому оценки начальных моментов порядка k вычисляются по формуле 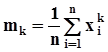.В частности, оценкой математического ожидания служит среднее арифметическое: 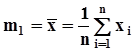.Точно так же с помощью интеграла Стилтьеса получим оценки центральных моментов: .

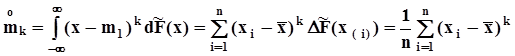В частности, оценка дисперсии вычисляется, как 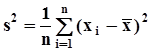.Эта же оценка может быть вычислена иначе с применением формулы из п. 1.6.2: 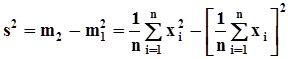.Эта формула бывает полезной при вычислении оценок на компьютере в темпе получения данных путем накопления оценок начальных моментов при получении каждого i - го результата измерений. Однако, здесь следует предостеречься от опасности, которая заключается в возможности получения отрицательного значения для 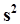. Это может произойти из-за погрешности округления, когда выборочные значения очень велики, а дисперсия генеральной совокупности по сравнению с ними очень мала.

28.Точечная оценка дисперсии по гистограмме, вывод формулы, поправка Шеппарда.2.3.2.2. Оценивание моментов по выборочной плотности распределения(по гистограмме), здесь для определения оценок моментов вместо плотности распределения генеральной совокупности будем использовать выборочную плотность, то есть гистограмму:- оценки начальных моментов

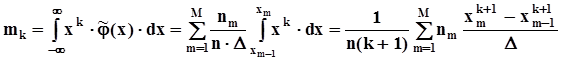,- оценки центральных моментов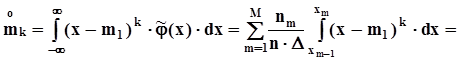 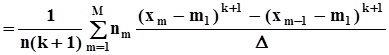.Понятно, что потери информации, вызванные группированием выборочных значений при построении гистограммы, снижают качество оценок по сравнению с оценками по выборочной функции распределения.Пользуясь этими общими формулами, найдем оценки математического ожидания и дисперсии. 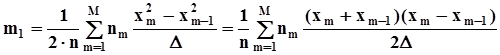.Поскольку

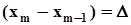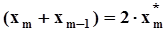, ,где 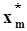- середина m - го отрезка, окончательно получим: 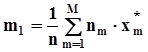.Оценка дисперсии.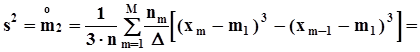 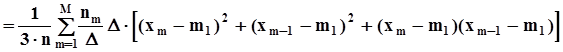.Используя равенство 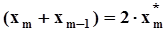, сделаем замены 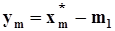, , 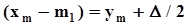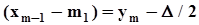.Тогда предыдущее равенство упрощается: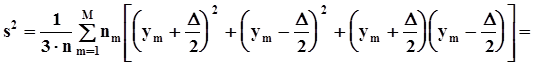 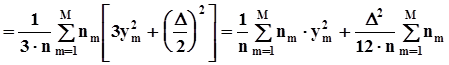.Окончательно получим: 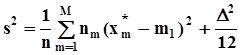.Слагаемое 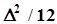называется поправкой Шеппарда.

29.Свойства точечных оценок, примеры смещенных и несмещенных, эффективных и состоятельных точечных оценок, ММП - оценка параметра экспоненциального распределения.2.3.4. Свойства точечных оценок.Поскольку выборочные значения (вектор выборочных значений) случайны на множестве исходов экспериментов, повторяющихся в неизменных условиях и в неизменном объеме, то оценки моментов и параметров законов распределения также случайны, а потому в качестве характеристик их свойств применяются вероятностные критерии.Применим общее обозначение для генеральных моментов и параметров случайных величин и их законов распределения - Q. Для обозначения оценок моментов и параметров, вычисляемых по выборке объема n, будем использовать обозначение 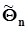. Важнейшими свойствами точечных оценок являются: несмещенность, эффективность, состоятельность. В последнее время возрастает роль четвертого свойства: устойчивости (resistance).a) Оценка момента (или параметра) является несмещенной, если ее математическое ожидание при фиксированном объеме выборки n равно оцениваемому генеральному моменту или параметру: 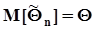.b) Оценка момента (или параметра) эффективна, если при фиксированном объеме выборки n она обладает минимальной дисперсией среди всех ценок данного момента (параметра): 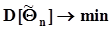.с) Оценка момента (или параметра) состоятельна, если с увеличением объема выборки nона стремится по вероятности к генеральному значению момента (или параметра), то есть, если при любом сколько угодно малом положительном e: 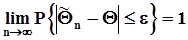.d) Устойчивые оценки - оценки, не чувствительные или малочувствительные к возмущениям в виде грубых промахов измерений, к погрешностям вычислений и т.п.Оценки могут быть:- несмещенные, эффективные, состоятельные,- несмещенные, но неэффективные,- эффективные, но смещенные,- смещенные при каждом фиксированномn , но состоятельные, такие оценки являются асимптотически несмещенными.

30.Разновидности оценок математического ожидания, их свойства, плотность распределения вероятностей среднего арифметического, ММП - оценка математического ожидания случайной величины, распределенной по Лапласу.2.3.4.1. Свойства оценок математического ожидания случайной величиныВыборка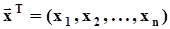извлечена из генеральной совокупности X, образованной случайной величиной x. Генеральные моменты: математическое ожидание M[x]= 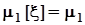, дисперсия 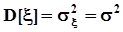. Для оценки математического ожидания используются несколько видов оценок. Наиболее популярной оценкой является среднее арифметическое значение 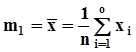.Среди других оценок назовем выборочную медиану 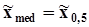и середину размаха 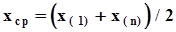, которые применяются в случаях, когда случайная величина x имеет симметричную плотность распределения.

Рассмотрим подробно свойства оценки 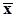.a)Проверим несмещенность среднего арифметического: 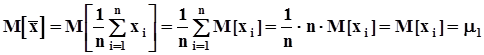,а это означает, что среднее арифметическое выборочных значений есть несмещенная оценка математического ожидания случайной величины независимо от вида закона распределения.b)Найдем дисперсию среднего арифметического, используя те же формулы п. 1.6.5 с учетом того, что- выборочные значения попарно независимы,- выборочные значения случайны на множестве групп экспериментов объемом n, и каждое из них распределено так же, как случайная величина x, каждое выборочное значениеимеет числовые характеристики генеральной совокупности. 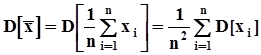.Поскольку выборочные значения 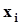, изъяты из одной генеральной совокупности, их дисперсии одинаковы. Поэтому 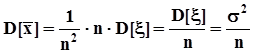.Среднеквадратическое значение среднего арифметического равно 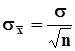.Из полученных соотношений видно, что обработка результатов многократных измерений путем вычисления среднего арифметического небесполезно, ибо показатель разброса значений средних арифметических убывает с увеличением объема выборки.Из последующего материала (п. 2.3.5) мы узнаем, что - среднее арифметическое - эффективная оценка математического ожидания нормальной случайной величины.- выборочная медиана - несмещенная оценка математического ожидания случайных величин с симметричной плотностью распределения и является эффективной оценкой математического ожидания случайной величины, распределенной по Лапласу (см. также п. 2.3.5).- середина размаха - несмещенная оценка математического ожидания случайных величин с симметричной плотностью распределения и является эффективной оценкой математического ожидания случайной величины, распределенной равномерно или по закону Arcsin.c)Проверим состоятельность среднего арифметического, как оценки математического ожидания.Применим неравенство Чебышева (п.1.6.8), приняв в качестве случайной величины xсреднее арифметическое 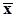с дисперсией 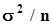. Из неравенства 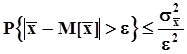следует противоположное ему: 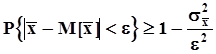.Поскольку среднее арифметическое есть несмещенная оценка математического ожидания, 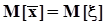. Поэтому 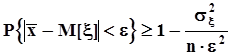.Каким бы малым не было e, его значение фиксировано, поэтому при n ®¥ вычитаемое в правой части неравенства стремится к нулю, а правая часть - к единице.Таким образом, состоятельность среднего арифметического, как оценки математического ожидания, доказана независимо от вида закона распределения.Мы получили пример полезного применения неравенства Чебышева, несмотря на грубость даваемой им оценки.Выборочная медиана и середина размаха - состоятельные оценки математического ожидания случайных величин с симметричной плотностью распределения.d)Плотность распределения среднего арифметического.Примем вначале, что выборка извлечена из нормальной генеральной совокупности 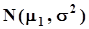. Тогда на множестве групп экспериментов каждое выборочное значение распределено также нормально, то есть 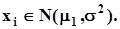В силу безграничной делимости нормального распределения сумма выборочных значений распределена нормально, а умножение ее на множитель 1/n приводит лишь к изменению масштаба. Таким образом, на основании свойств a) и b) получаем, что .

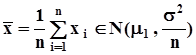31.Точечная оценка дисперсии при известном и неизвестном математическом ожидании, свойства, плотность распределения оценки дисперсии нормальной генеральной совокупности (вывод), график.

2.3.4.2. Свойства оценок дисперсии.a) Рассмотрим вначале случай, когда математическое ожидание исследуемой случайной величины известно и равно 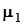. Дисперсия генеральной совокупности X, образованной случайной величиной x, равна 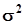.В этом случае оценка дисперсии вычисляется по формуле 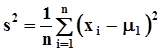.Проверим несмещенность этой оценки. 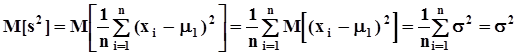.При условии, когда математическое ожидание исследуемой случайной величины известно, оценка несмещена.

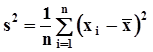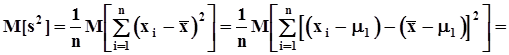
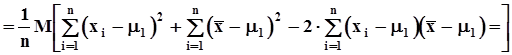
b) Обычно на практике математическое ожидание исследуемой случайной величины неизвестно. В этом случае вместо него приходится использовать оценку, например, среднее арифметическое: .Проверим несмещенность этой оценки. 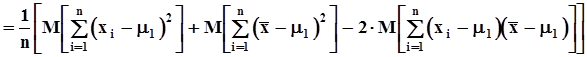.Первое слагаемое во внешних квадратных скобках есть сумма дисперсий генеральной совокупности, их в этой сумме n штук, то есть первое слагаемое равно 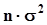. Второе слагаемое есть сумма дисперсий средних арифметических, оно равно 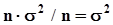. Конструкция вычитаемого сложнее. Рассмотрим его отдельно. Запишем второй сомножитель под знаком суммы в виде: 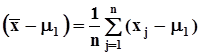.В справедливости такой записи можно убедиться, раскрыв скобки и подсчитав каждую сумму по отдельности.Сделаем подстановку: 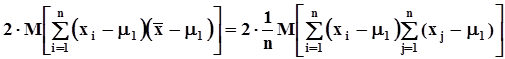.Здесь в квадратных скобках суммируются произведения биномов, отличающихся только индексом. В результате внутри квадратных скобок образуется сумма 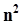слагаемых, среди которых встречаются слагаемые, сомножители которых имеют одинаковые индексы i = j (таких слагаемых nштук), и слагаемые, сомножители которых имеют разные индексы (таких слагаемых 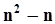штук).