Дисперсия параметра оптимизации
При подсчете дисперсии параметра оптимизации квадрат разности между значением Y в каждом опыте и средним значением из m повторных наблюдений 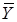 нужно просуммировать по числу опытов в матрице N, а затем разделить на N(m - 1):
нужно просуммировать по числу опытов в матрице N, а затем разделить на N(m - 1):
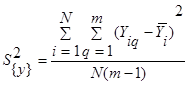 (7) Такой формулой можно пользоваться в случаях, когда число повторных опытов одинаково во всей матрице. Для 2-х повторных опытов формула принимает вид
(7) Такой формулой можно пользоваться в случаях, когда число повторных опытов одинаково во всей матрице. Для 2-х повторных опытов формула принимает вид
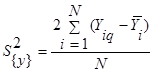 (8) В дисперсию воспроизводимости проще считать при равенстве повторных опытов. В случае, когда число повторных опытов неодинаково (отброс грубых наблюдений) приходится пользоваться средним взвешенным значением дисперсий, взятым с учетом степеней свободы.
(8) В дисперсию воспроизводимости проще считать при равенстве повторных опытов. В случае, когда число повторных опытов неодинаково (отброс грубых наблюдений) приходится пользоваться средним взвешенным значением дисперсий, взятым с учетом степеней свободы.
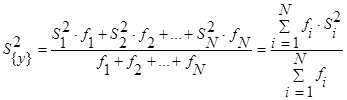 , (**)
, (**)
где 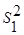 - дисперсия 1-го опыта,
- дисперсия 1-го опыта, 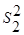 - дисперсия 2-го опыта и т.д.
- дисперсия 2-го опыта и т.д.
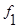 -число степеней свободы в 1-ом опыте, равном числу параллельных опытов m минус 1.
-число степеней свободы в 1-ом опыте, равном числу параллельных опытов m минус 1.
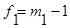 ,
, 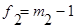 и т.д.
и т.д.
Формулами (7) и (9) можно пользоваться только в том случае, если дисперсии однородны. Однородность дисперсий означает, что среди всех суммируемых дисперсий нет таких, которые бы значительно превышали все остальные.
Проверка однородности дисперсий
Особое внимание следует уделять проверке однородности дисперсий, т.к. это одна из предпосылок, лежащих в основе регресс-анализа. Для проверки однородности дисперсий можно пользоваться критериями Фишера, Кохрена или Бартлета. Проверка однородности дисперсий производится с помощью различных статистических критериев, из которых простейшим является критерий Фишера, предназначенный для сравнения 2-х дисперсий. Критерий Фишера (F - критерий) представляет отношение большей дисперсии к меньшей. Полученная величина сравнивается с табличной величиной F -критерия.
Если сравниваемое количество дисперсий больше 2-х и одна дисперсия значительно превышает остальные, можно воспользоваться критерием Кохрена. Он пригоден для случаев, когда во всех точках имеется одинаковое число опытов. При этом подсчитывается дисперсия в каждой горизонтальной строке матрицы:
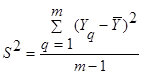 (10)
(10)
а затем из всех дисперсий находится наибольшее 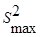 , которая делится на сумму всех дисперсий.
, которая делится на сумму всех дисперсий. 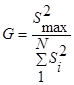 (11)
(11)
Гипотеза об однородности дисперсий подтверждается, если экспериментальное значение критерия G не превышает табличного значения. После этого можно усреднять дисперсии и пользоваться формулой (*).
Рандомизация опытов
Чтобы исключить влияние систематических ошибок, вызванных внешними условиями (колебанием t°, партий сырья, лаборанта и т.д.), рекомендуется случайная последовательность проведения опытов. Random - случайный. Опыты необходимо рандомизировать во времени.
