Учебно-методический центр по образованию
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА УПРАВЛЕНИЕ УЧЕБНЫХ ЗАВЕДЕНИЙ И ПРАВОВОГО ОБЕСПЕЧЕНИЯ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
УЧЕБНО-МЕТОДИЧЕСКИЙ ЦЕНТР ПО ОБРАЗОВАНИЮ
НА ЖЕЛЕЗНОДОРОЖНОМ ТРАНСПОРТЕ»
ЕН.01 МАТЕМАТИКА
Методические указания и контрольные задания
для студентов-заочников образовательных учреждений среднего профессионального образования железнодорожного транспорта по специальностям
140409 Электроснабжение (по отраслям).
190623 Техническая эксплуатация подвижного состава железных дорог
Специализация
190623.01 Устройства и электрические аппараты электроподвижного состава
190623.03 Установки и электрические аппараты вагонов.
Петрозаводск
2012г.
| Рассмотрено на заседании ЦК преподавателей Математических и естественно-научных дисциплин протокол № ____ от «____»________2012г. Председатель_____________/Ганеева Е. И./ | «УТВЕРЖДАЮ» Зам. директора по учебной работе ПКЖТ- филиал ПГУПС __________________М.Г.Дмитриев «______»_________________2012г. |
Методические указания составлены в соответствии с рабочей программой учебной дисциплины «математика» для специальностей
140409 Электроснабжение (по отраслям)
190623 Техническая эксплуатация подвижного состава железных дорог
Автор Клестова Е.Д. - преподаватель ПКЖТ – филиала ПГУПС
Рецензенты:
Яковцева Г.Б. - преподаватель ПКЖТ – филиал ПГУПС
Фалина Т. Б.- преподаватель высшей категории Петрозаводского лесотехнического техникума
ВВЕДЕНИЕ
Программа учебной дисциплины является частью основной профессиональной образовательной программы в соответствии с ФГОС по специальности СПО 140409 Электроснабжение (по отраслям) (базовая подготовка), входящей в состав укрупнённой группы профессий 140000 Энергетика, энергетическое машиностроение и электротехника, 190623 Техническая эксплуатация подвижного состава железных дорог. Специализация 190623.03 Установки и электрические аппараты вагонов, входящей в состав укрупненной группы профессий 190000 Транспортные средства.
Программа учебной дисциплины может быть использована в профессиональной подготовке, повышении квалификации и переподготовке рабочих и служащих по профессиям:
19825 Электромонтёр контактной сети.
19842 Электромонтёр по обслуживанию подстанции.
19855 Электромонтёр по ремонту воздушных линий электропередачи.
19859 Электромонтёр по ремонту и монтажу кабельных линий.
19867 Электромонтёр по эксплуатации распределительных сетей.
19888 Электромонтёр тяговой подстанции.
15859 Оператор по обслуживанию и ремонту вагонов и контейнеров;
16269 Осмотрщик вагонов;
16275 Осмотрщик-ремонтник вагонов.
В результате освоения учебной дисциплины обучающийся должен
уметь:
· решать прикладные задачи в области профессиональной деятельности.
В результате освоения учебной дисциплины обучающийся должен
знать:
· значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы;
· основные математические методы решения прикладных задач в области профессиональной деятельности;
· основные понятия и методы математического анализа, линейной алгебре, теории комплексных чисел, теории вероятностей и математической статистики.
· основы интегрального и дифференциального исчисления.
Количество часов на освоение программы учебной дисциплины
максимальной учебной нагрузки обучающегося 99 часов, в том числе:
- обязательной аудиторной учебной нагрузки обучающегося 14 часов;
- самостоятельной работы обучающегося 85часов.
В данном пособии для студентов заочной формы обучения содержится одна контрольная работа и методические указания к выполнению контрольной работы.
Тематический план и содержание учебной дисциплины «Математика»
| Наименование разделов и тем | Содержание учебного материала, практические занятия, самостоятельная работа обучающихся | Объем часов | Уровень освоения | ||||
| Раздел 1. Линейная алгебра | |||||||
| Тема 1.1. Матрицы и определители | Содержание учебного материала: | ||||||
| Понятие матрицы и определителя. Вычисление определителей второго, третьего порядков. Свойства определителей. Разложение определителя по элементам строки. Вычисление определителей четвертого порядка. | |||||||
| Практические занятия №1-2 | |||||||
| Выполнение операций над матрицами | |||||||
| Вычисление определителей третьего и четвёртого порядков | |||||||
| Самостоятельная работа обучающихся | |||||||
| Понятие матрицы и определителя. Вычисление определителей второго, третьего порядков. Свойства определителей. Разложение определителя по элементам строки. Вычисление определителей четвертого порядка. Выполнение операций над матрицами Практические занятия №1-2 Выполнение операций над матрицами Вычисление определителей третьего и четвёртого порядков | |||||||
| Тема 1.2. Системы линейных уравнений | Содержание учебного материала: | ||||||
| Понятие системы линейных уравнений. Матричная форма записи линейных уравнений. Теорема Крамера. Метод Гаусса для решения системы линейных уравнений. | |||||||
| Практические занятия №3-4 | |||||||
| Решение систем линейных уравнений методом Крамера | |||||||
| Решение систем линейных уравнений методом Гаусса | |||||||
| Самостоятельная работа обучающихся | |||||||
| Понятие системы линейных уравнений. Матричная форма записи линейных уравнений. Теорема Крамера. Метод Гаусса для решения системы линейных уравнений. Решение систем линейных уравнений методом Крамера Решение систем линейных уравнений методом Гаусса Практические занятия №3-4 Решение систем линейных уравнений методом Крамера Решение систем линейных уравнений методом Гаусса | |||||||
| Раздел 2. Комплексные числа | |||||||
| Тема 2.1. Три формы комплексного числа. | Содержание учебного материала | ||||||
| Алгебраическая, тригонометрическая и показательная формы комплексных чисел. Определение, основные понятия, действия над комплексными числами. Комплексная координатная плоскость Выполнение действий над комплексными числами в алгебраической форме. Построение геометрической модели. Решение заданий по переходу от алгебраической формы комплексного числа к тригонометрической и показательной. Решение заданий по переходу от тригонометрической и показательной форм комплексного числа к алгебраической . | |||||||
| Практические занятия № 5-7 | |||||||
| Выполнение действий над комплексными числами в алгебраической форме. Построение геометрической модели. | |||||||
| Решение заданий по переходу от алгебраической формы комплексного числа к тригонометрической и показательной. Решение заданий по переходу от тригонометрической и показательной форм комплексного числа к алгебраической . | |||||||
| Выполнение действий над комплексными числами в трёх формах | |||||||
| Самостоятельная работа обучающихся | |||||||
| Выполнение действий над комплексными числами в алгебраической форме. Построение геометрической модели. Решение заданий по переходу от алгебраической формы комплексного числа к тригонометрической и показательной. Решение заданий по переходу от тригонометрической и показательной форм комплексного числа к алгебраической . Практические занятия № 5-6 Выполнение действий над комплексными числами в алгебраической форме. Построение геометрической модели. Решение заданий по переходу от алгебраической формы комплексного числа к тригонометрической и показательной. Решение заданий по переходу от тригонометрической и показательной форм комплексного числа к алгебраической . | |||||||
| Раздел 3. Математический анализ | |||||||
| Тема 3.1. Дифференциальное и интегральное исчисление | Содержание учебного материала | ||||||
| Функции одной независимой переменной. Пределы. Непрерывность функций. Производная, геометрический смысл. Исследование функций. Приложения производной. | |||||||
| Неопределенный интеграл. Непосредственное интегрирование Замена переменной. Определенный интеграл. Вычисление определенного интеграла Геометрический смысл определенного интеграла. Функции нескольких переменных. Приложения интеграла к решению прикладных задач. Частные производные | |||||||
| Практические занятия №8-9 | |||||||
| Решение задач на приложения производной. | |||||||
| Решение задач на приложения определённого интеграла. | |||||||
| Самостоятельная работа обучающихся | |||||||
| Функции одной независимой переменной. Пределы. Непрерывность функций. Производная, геометрический смысл. Исследование функций. Неопределенный интеграл. Непосредственное интегрирование. Замена переменной. Определенный интеграл. Вычисление определенного интеграла. Геометрический смысл определенного интеграла. Функции нескольких переменных. Приложения интеграла к решению прикладных задач. Частные производные. | |||||||
| Тема 3.2. Обыкновенные дифференциальные уравнения | Содержание учебного материала | ||||||
| Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения с разделяющимися переменными. Общие и частые решения. Однородные дифференциальные уравнения первого порядка. Линейные однородные уравнения второго порядка с постоянными коэффициентами. | |||||||
| Практическое занятие №10-11 | |||||||
| Решение дифференциальных уравнений первого порядка с разделяющимися переменными | |||||||
| Решение линейных однородных уравнений второго порядка с постоянными коэффициентами. | |||||||
| Самостоятельная работа обучающихся | |||||||
| Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения с разделяющимися переменными. Общие и частые решения. Однородные дифференциальные уравнения первого порядка. Линейные однородные уравнения второго порядка с постоянными коэффициентами. Практическое занятие №10-11 Решение дифференциальных уравнений первого порядка с разделяющимися переменными Решение линейных однородных уравнений второго порядка с постоянными коэффициентами | |||||||
| Тема 3.3. Ряды | Содержание учебного материала | ||||||
| Числовые ряды. Сходимость и расходимость числовых рядов. Признак сходимости Даламбера. Знакопеременные ряды. Абсолютная и условная сходимость рядов. Интегральный признак Коши. Признак Лейбница. Степенные ряды. Ряды Фурье. | |||||||
| Практическое занятие №12 | |||||||
| Разложение функций в ряд Фурье Решение задач на исследование сходимости и расходимости числовых рядов. | |||||||
| Самостоятельная работа обучающихся | |||||||
| Числовые ряды. Сходимость и расходимость числовых рядов. Признак сходимости Даламбера. Знакопеременные ряды. Абсолютная и условная сходимость рядов. Интегральный признак Коши. Признак Лейбница. Степенные ряды. Ряды Фурье. Практическое занятие №12 Разложение функций в ряд Фурье. Решение задач на исследование сходимости и расходимости числовых рядов. | |||||||
| Раздел 4. Приближенные вычисления | |||||||
| Тема 4.1. Приближенные вычисления | Содержание учебного материала | ||||||
| Точные и приближенные значения величин. Абсолютная и относительная погрешности, граница погрешности. Классификация погрешности. Погрешности вычислений с приближенными данными | |||||||
| Практическое занятие №13 | |||||||
| Расчет абсолютной и относительной погрешности , границы погрешности. | |||||||
| Самостоятельная работа обучающихся | |||||||
| Точные и приближенные значения величин. Абсолютная и относительная погрешности, граница погрешности. Классификация погрешности. Погрешности вычислений с приближенными данными. | |||||||
| Раздел 5 Основы дискретной математики | |||||||
| Тема 5.1. -5.2. Основы теории множеств. Основы теории графов. | Содержание учебного материала | ||||||
| Множество и его элементы. Пустое множество, подмножества некоторого множества. Операции над множествами: Отображение множеств. Понятие функции и способы ее задания, композиция функций. Отношения их виды и свойства. Диаграмма Венна. Числовые множества. Определение графа, виды графов: полные, неполные. Элементы графа: вершины, ребра; степень вершины. Применение теории графов при решении профессиональных задач: в экономике и логистике. | |||||||
| Практическое занятие №14 | |||||||
| Построение графа по условию ситуационных задач: в управлении инфраструктурами на транспорте; в структуре взаимодействия различных видов транспорта, в формировании технологического цикла оказания услуг на транспорте. | |||||||
| Самостоятельная работа обучающихся | |||||||
| Множество и его элементы. Пустое множество, подмножества некоторого множества. Операции над множествами: Отображение множеств. Понятие функции и способы ее задания, композиция функций. Отношения их виды и свойства. Диаграмма Венна. Числовые множества. Определение графа, виды графов: полные, неполные. Элементы графа: вершины, ребра; степень вершины. Применение теории графов при решении профессиональных задач: в экономике и логистике. Практическое занятие №14 Построение графа по условию ситуационных задач: в управлении инфраструктурами на транспорте; в структуре взаимодействия различных видов транспорта, в формировании технологического цикла оказания услуг на транспорте. | |||||||
| Раздел 6. Основы теории вероятности и математической статистики | |||||||
| Тема 6.1. Вероятность. Теоремы сложения и умножения вероятностей | Содержание учебного материала | ||||||
| Понятие события и вероятности события. Достоверные и невозможные события. Классическое определение вероятности. Теорема сложения вероятностей. Теорема умножения вероятностей. Применение теории вероятности при решении профессиональных задач | |||||||
| Практическое занятие №15 | |||||||
| Решение простейших задач на определение вероятности события. Решение задач на определение вероятности события с использованием теоремы сложения и умножения вероятностей. | |||||||
| Самостоятельная работа обучающихся | |||||||
| Понятие события и вероятности события. Достоверные и невозможные события. Классическое определение вероятности. Теорема сложения вероятностей. Теорема умножения вероятностей. Применение теории вероятности при решении профессиональных задач Практическое занятие №15 Решение простейших задач на определение вероятности события. Решение задач на определение вероятности события с использованием теоремы сложения и умножения вероятностей. | |||||||
| Тема 6.2. Случайная величина, ее функция распределения | Содержание учебного материала | ||||||
| Случайная величина. Дискретная и непрерывная случайные величины. Закон распределения случайной величины. | |||||||
| Практическое занятие №16 | |||||||
| По заданному условию построить ряд распределения случайной величины согласно закону распределения дискретной случайной величины. | |||||||
| Самостоятельная работа обучающихся | |||||||
| Случайная величина. Дискретная и непрерывная случайные величины. Закон распределения случайной величины. Практическое занятие №16 По заданному условию построить ряд распределения случайной величины согласно закону распределения дискретной случайной величины. | |||||||
| Тема 6.3. Математическое ожидание и дисперсия случайной величины | Содержание учебного материала | ||||||
| Математическое ожидание дискретной случайной величины. Дисперсия случайной величины. Среднее квадратичное отклонение случайной величины. | |||||||
| Практические занятия №17 | |||||||
| Нахождение математического ожидания и дисперсии дискретной случайной величины по закону распределения. Решение задач на нахождение математического ожидания и дисперсии при оценке эффективности заказов и обслуживания потребителей услуг и при оценке систем надежности, безопасности и качества услуг на железнодорожном транспорте. | |||||||
| Самостоятельная работа обучающихся | |||||||
| Математическое ожидание дискретной случайной величины. Дисперсия случайной величины. Среднее квадратичное отклонение случайной величины. Практические занятия №17 Нахождение математического ожидания и дисперсии дискретной случайной величины по закону распределения. Решение задач на нахождение математического ожидания и дисперсии при оценке эффективности заказов и обслуживания потребителей услуг и при оценке систем надежности, безопасности и качества услуг на железнодорожном транспорте. | |||||||
| Раздел 7. Основные численные методы | |||||||
| Тема 7.1. Численное интегрирование | Содержание учебного материала | ||||||
| Формулы прямоугольников. Формула трапеций. Формула Симпсона. Абсолютная погрешность при численном интегрировании | |||||||
| Практическое занятие №18 | |||||||
| Вычисление интегралов по формулам прямоугольников, трапеций и формуле Симпсона. Оценка погрешности. | |||||||
| Самостоятельная работа обучающихся | |||||||
| Формулы прямоугольников. Формула трапеций. Формула Симпсона. Абсолютная погрешность при численном интегрировании. Практическое занятие №18 Вычисление интегралов по формулам прямоугольников, трапеций и формуле Симпсона. Оценка погрешности. | |||||||
| Тема 7.2.-7.3. Численное дифференцирование. Численное решение обыкновенных дифференциальных уравнений. | Содержание учебного материала | ||||||
| Численное дифференцирование. Формулы приближенного дифференцирования, основанные на интерполяционных формул Ньютона. Погрешность в определении производной. Построение интегральной кривой. Метод Эйлера. | |||||||
| Практические занятия №19 | |||||||
| Решение задач на нахождение по таблично заданной функции (при n=2), функции, заданной аналитически. Решение задач на применение интерполяционных формул Ньютона | |||||||
| Практическое занятие№20 | |||||||
| Решение обыкновенных дифференциальных уравнений методом Эйлера. | |||||||
| Самостоятельная работа обучающихся | |||||||
| Численное дифференцирование. Формулы приближенного дифференцирования, основанные на интерполяционных формул Ньютона. Погрешность в определении производной. Построение интегральной кривой. Метод Эйлера. Практические занятия №19 Решение задач на нахождение по таблично заданной функции (при n=2), функции, заданной аналитически. Решение задач на применение интерполяционных формул Ньютона Практическое занятие№20 Решение обыкновенных дифференциальных уравнений методом Эйлера. | |||||||
| Домашняя контрольная работа. | |||||||
| Всего | |||||||
ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ №1
Задание на контрольную работу №1 составлено в 100 вариантах. Номер варианта определяется двумя последними цифрами шрифта студента по таблице 1.
Таблица 1.
Таблица вариантов:
| Вариант | Номер задач | Вариант | Номер задач |
| 7, 26, 69, 82, 101 | 1, 35, 55, 76, 110 | ||
| 14, 29, 54, 89, 104 | 2, 29, 54, 77, 104 | ||
| 20, 33, 59, 95, 108 | 3, 26, 51, 78, 101 | ||
| 9, 43, 67, 84, 118 | 4, 30, 56, 79, 105 | ||
| 12, 37, 65, 87, 112 | 11, 31, 52, 86, 106 | ||
| 10, 30, 58, 85, 105 | 9, 33, 74, 84, 108 | ||
| 19, 39, 68, 94, 114 | 7, 34, 53, 82, 109 | ||
| 11, 34, 60, 86, 109 | 8, 27, 57, 83, 102 | ||
| 15, 28, 64, 90, 103 | 5, 35, 58, 80, 110 | ||
| 2, 27, 53, 77, 102 | 23, 48, 73, 98, 123 | ||
| 4, 41, 52, 79, 116 | 25, 49, 72, 100, 124 | ||
| 18, 47, 51, 93, 122 | 6, 43, 67, 81, 118 | ||
| 5, 45, 66, 80, 120 | 10, 47, 71, 85, 122 | ||
| 21, 49, 62, 96, 124 | 12, 28, 53, 87, 103 | ||
| 25, 35, 61, 100, 110 | 24, 30, 56, 99, 105 | ||
| 17, 40, 56, 92, 115 | 22, 32, 57, 97, 107 | ||
| 8, 50, 63, 83, 125 | 13, 38, 63, 88, 113 | ||
| 23, 44, 71, 98, 119 | 23, 37, 64, 98, 112 | ||
| 1, 31, 55, 76, 106 | 14, 39, 65, 89, 114 | ||
| 6, 42, 70, 81, 117 | 22, 41, 66, 97, 116 | ||
| 3, 46, 74, 78, 121 | 21, 43, 68, 96,118 | ||
| 22, 48, 73, 97, 123 | 15, 44, 67, 90, 119 | ||
| 13, 38, 75, 88, 113 | 20, 42, 69, 95, 117 | ||
| 24, 36, 72, 99, 111 | 19, 45, 70, 94, 120 | ||
| 16, 32, 57, 91, 107 | 18, 46, 71, 93, 121 | ||
| 4. 34, 68, 79, 109 | 7, 48, 69, 82, 123 | ||
| 2, 39, 58, 77, 114 | 1, 39, 54, 76, 114 | ||
| 15, 35, 65, 90, 110 | 3, 26, 68, 78, 101 | ||
| 11, 37, 67, 86, 112 | 24, 34, 70, 99, 109 | ||
| 19, 43, 59, 94, 118 | 2, 40, 55, 77, 115 | ||
| 10, 33, 54, 85, 108 | 21, 31, 51, 96, 106 | ||
| 7, 43, 65, 82, 118 | 11, 35, 65, 86, 110 | ||
| 14, 34, 64, 89, 109 | 17, 44, 59, 92, 119 | ||
| 1, 38, 72, 76, 113 | 5, 50, 75, 80, 125 | ||
| 6, 36, 57, 81, 111 | 23, 38, 58, 98, 113 | ||
| 23, 46, 74, 98, 121 | 12, 28, 53, 87, 103 | ||
| 16, 29, 75, 91, 104 | 8, 40, 63, 83, 115 | ||
| 24, 29, 59, 99, 104 | 10, 42, 52, 85, 117 | ||
| 21, 47, 53, 96, 122 | 6, 39, 53, 81, 114 | ||
| 18, 28, 60, 93, 103 | 16, 32, 57, 91, 107 | ||
| 3, 31, 63, 78, 106 | 13, 45, 60, 88, 120 | ||
| 5, 41, 51, 80, 116 | 14, 26, 56, 89, 101 | ||
| 8, 44, 70, 83, 119 | 22, 37, 62, 97, 112 | ||
| 9, 39, 74, 84, 114 | 4, 43, 61, 79, 118 | ||
| 12, 32, 75, 87, 107 | 18, 37, 56, 93, 112 | ||
| 1, 26, 51, 76, 101 | 20, 36, 67, 95, 111 | ||
| 5, 30, 55, 80, 105 | 15, 27, 66, 90, 102 | ||
| 4, 29, 54, 79, 104 | 9, 50, 71, 84, 125 | ||
| 8, 33, 63, 83, 108 | 19, 49,58, 94, 124 | ||
| 25, 50, 75, 100, 125 | 25, 34, 74, 100, 109 |
КОНТРОЛЬНАЯ РАБОТА.
1–10. Выполните действия в алгебраической форме. Результат запишите в тригонометрической и показательной формах:
1. 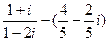 . 2. . 2. 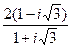 . 3. . 3. 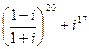 . 4. . 4. 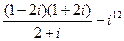 . 5. . 5. 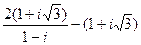 | 6. 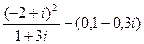 7. 7. 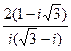 8. 8. 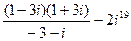 9. 9. 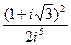 10. 10. 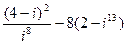 . . |
11-16. Выполните действия в тригонометрической форме. Результат запишите в показательной и алгебраической формах:
11. 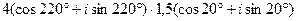 . 12. . 12. 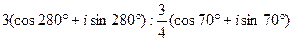 . 13. . 13. 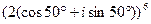 . . | 14. 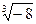 . 15. . 15. 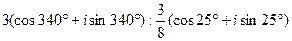 . 16. . 16. 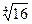 . . |
17–25. Запишите комплексное число в тригонометрической и алгебраической формах:
17. 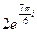 . 18. . 18. 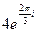 . 19. . 19. 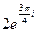 . . | 20. 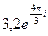 . 21. . 21. 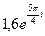 . 22. . 22. 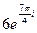 | 23. 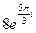 . 24. . 24. 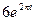 25. 25. 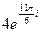 |
26. Найдите производную функции 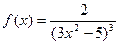 и вычислите
и вычислите 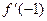 .
.
27. Найдите производную функции 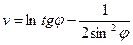 и вычислите
и вычислите 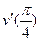 .
.
28. Найдите производную функции 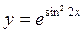 и вычислите
и вычислите 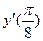 .
.
29. Найдите производную функции 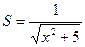 и вычислите
и вычислите 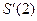 .
.
30. Найдите производную функции 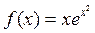 и вычислите
и вычислите 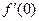 .
.
31. Найдите производную функции 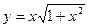 и вычислите
и вычислите 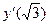 .
.
32. Найдите производную функции 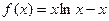 и вычислите
и вычислите 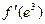 .
.
33. Найдите производную функции 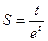 и вычислите
и вычислите 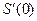 .
.
34. Найдите производную функции 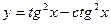 и вычислите
и вычислите 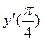 .
.
35. Найдите вторую производную функции 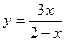 и вычислите
и вычислите 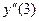 .
.
36. Найдите производную функции 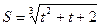 и вычислите
и вычислите 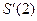 .
.
37. Найдите производную функции 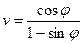 и вычислите
и вычислите 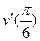 .
.
38. Найдите вторую производную функции 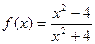 и вычислите
и вычислите 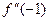 .
.
39. Найдите производную функции 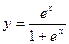 и вычислите
и вычислите 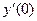 .
.
40. Найдите производную функции 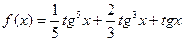 и вычислите
и вычислите 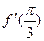 .
.
41. Найдите производную функции 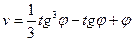 и вычислите
и вычислите 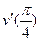 .
.
42. Найдите вторую производную функции 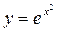 и вычислите
и вычислите 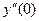 .
.
43. Найдите вторую производную функции 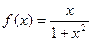 и вычислите
и вычислите 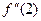 .
.
44. Найдите производную функции 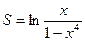 и вычислите
и вычислите 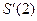 .
.
45. Найдите вторую производную функции 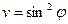 и вычислите
и вычислите 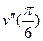 .
.
46. Найдите производную функции 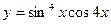 и вычислите
и вычислите 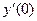 .
.
47. Найдите производную функции 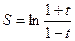 и вычислите
и вычислите 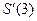 .
.
48. Найдите производную функции 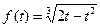 и вычислите
и вычислите 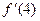 .
.
49. Найдите вторую производную функции 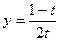 и вычислите
и вычислите 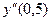 .
.
50. Найдите производную функции 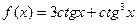 и вычислите
и вычислите 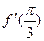 .
.
51. Постройте график функции 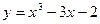 .
.
52. Резервуар емкостью 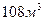 с квадратным основанием, открытый сверху, нужно покрыть эмалью. Каковы должны быть размеры резервуара, чтобы израсходовать для этого минимальное количество эмали?
с квадратным основанием, открытый сверху, нужно покрыть эмалью. Каковы должны быть размеры резервуара, чтобы израсходовать для этого минимальное количество эмали?
53. Постройте график функции 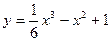 .
.
54. Число 25 запишите в виде произведения двух положительных чисел, сумма которых наименьшая.
55. Тело движется прямолинейно по закону 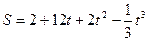 . Найдите максимальную скорость движения тела.
. Найдите максимальную скорость движения тела.
56. Какие размеры должен иметь цилиндр, площадь полной поверхности которого 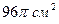 , чтобы его объем был наибольшим?
, чтобы его объем был наибольшим?
57. Путь S в метрах, пройденный телом за t секунд при прямолинейном движении, определяется уравнением 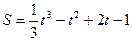 . Найдите скорость и ускорение в конце третьей секунды.
. Найдите скорость и ускорение в конце третьей секунды.
58. Докажите, что из всех прямоугольников, имеющих периметр 32см, наибольшую площадь имеет квадрат.
59. Найдите наибольшее и наименьшее значения функции 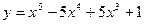 на отрезке
на отрезке 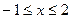 .
.
60. Постройте график функции 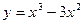 .
.
61. Число 50 представьте в виде суммы двух положительных слагаемых так, что бы произведение этих чисел было наибольшим.
62. Составьте уравнение касательной к графику функции 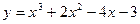 в точке с абсциссой
в точке с абсциссой 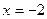 .
.
63. Какой из цилиндров с объемом 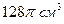 имеет наименьшую полную поверхность?
имеет наименьшую полную поверхность?
64. Постройте график функции 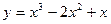 .
.
65. Требуется изготовить ящик с крышкой, объем которого равен 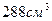 , а стороны основания относятся как 1:3. Каковы должны быть размеры ящика, что бы его полная поверхность была наименьшей?
, а стороны основания относятся как 1:3. Каковы должны быть размеры ящика, что бы его полная поверхность была наименьшей?
66. Около стены нужно сделать забор, чтобы огородить прямоугольный участок земли наибольшей площади. Общая длина забора 60м. Найдите длину части забора, параллельной стене.
67. Найдите наибольшее и наименьшее значения функции 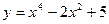 на отрезке
на отрезке 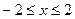 .
.
68. Гипотенуза прямоугольного треугольника равна 8см. Найдите длину каждого катета, если площадь треугольника должна быть наибольшей.
69. Напишите уравнения касательных к кривой 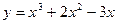 в точках ее пересечения с осью Ох.
в точках ее пересечения с осью Ох.
70. Докажите, что из всех прямоугольников с площадью 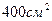 квадрат имеет наименьший периметр.
квадрат имеет наименьший периметр.
71. Найдите наибольшее и наименьшее значения функции 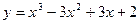 на отрезке
на отрезке 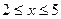 .
.
72. Из всех прямоугольных параллелепипедов, у которых в основании лежит квадрат и площадь полной поверхности равна 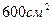 , найдите параллелепипед наибольшего объема и определите его размеры.
, найдите параллелепипед наибольшего объема и определите его размеры.
73. Постройте график функции 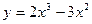 .
.
74. Какое положительное число, будучи сложено с обратным ему числом, дает наименьшую сумму?
75. Каковы должны быть размеры цилиндрического сосуда емкостью 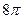 литров, открытого сверху, чтобы на его изготовление потребовалось наименьшее количество материала?
литров, открытого сверху, чтобы на его изготовление потребовалось наименьшее количество материала?
76–100. Найдите интегралы:
76. а) 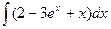 . . | б) 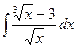 . . |
77. а) 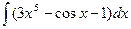 . . | б) 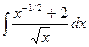 . . |
78. а) 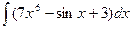 . . | б) 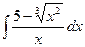 . . |
79. а) 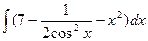 . . | б) 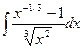 . . |
80. а) 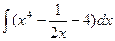 . . | б) 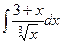 . . |
81. а) 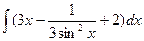 . . | б) 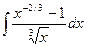 . . |
82. а) 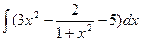 . . | б) 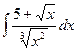 . . |
83. а) 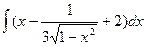 . . | б) 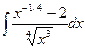 . . |
84. а) 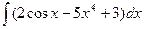 . . | б) 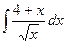 . . |
85. а) 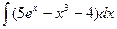 . . | б) 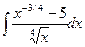 . . |
86. а) 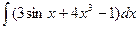 . . | б) 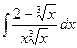 . . |
87. а) 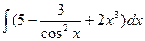 . . | б)  . . |
88. а) 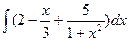 . . | б) 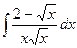 . . |
89. а) 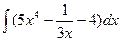 . . | б) 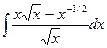 . . |
90. а) 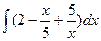 . . | б) 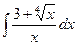 . . |
91. а) 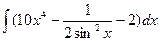 . . | б) 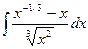 . . |
92. а) 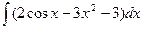 . . | б) 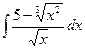 . . |
93. а) 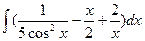 . . | б) 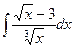 . . |
94. а) 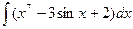 . . | б) 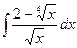 . . |
95. а) 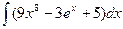 . . | б) 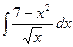 . . |
96. а) 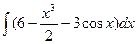 . . | б) 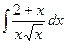 . . |
97. а) 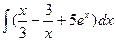 . . | б) 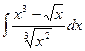 . . |
98. а) 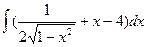 . . | б) 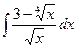 . . |
99. а) 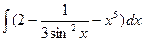 . . | б) 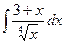 . . |
100. а) 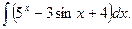 | б) 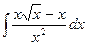 . . |
101–111. Сделайте чертеж и вычислите площадь фигуры, ограниченной данными линиями:
101. 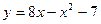 и осью Ох. 102 и осью Ох. 102 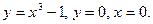 103. 103. 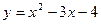 и осью Ох. 104. и осью Ох. 104. 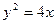 и и 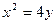 105. 105. 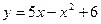 и осью Ох. 106. и осью Ох. 106. 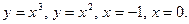 | 107. 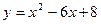 и осью Ох. 108. и осью Ох. 108. 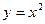 и и 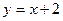 109. 109. 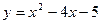 и осью Ох. 110. и осью Ох. 110. 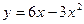 и осью Ох. 111. и осью Ох. 111. 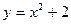 и и 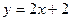 |
112–115. Сделайте чертеж и вычислите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной данными линиями:
112. 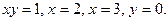 113. 113. 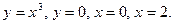 | 114. 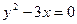 и и 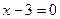 115. 115. 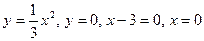 |
116–118. Сделайте чертеж и вычислите объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной данными линиями:
116. 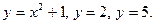
117. 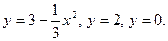
118. 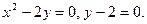
119. Тело брошено с поверхности земли вертикально вверх со скоростью 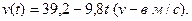 Вычислите наибольшую высоту подъема тела.
Вычислите наибольшую высоту подъема тела.
120. Скорость прямолинейного движения тела задана уравнением
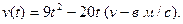 Вычислите его путь, пройденный за четвертую секунду.
Вычислите его путь, пройденный за четвертую секунду.
121. Вычислите работу, которую нужно совершить при растяжении пружины на 8см, если сила 3Н растягивает пружину на 1см.
122. Сила 6Н растягивает пружину на 8см. Какую работу она производит?
123. При сжатии пружины на 4см необходимо совершить работу 9,81Дж. Какую работу надо произвести для сжатия пружины на 10см?
124. Вычислите силу давления ртути, наполняющей стакан цилиндрической формы, на его боковую поверхность, если высота стакана 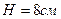 , радиус основания
, радиус основания 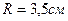 , плотность ртути
, плотность ртути 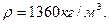
125. Вычислите силу давления воды на погруженную вертикально в нее пластинку, имеющую форму треугольника с основанием 10см и высотой 5см, предполагая, что вершина этого треугольника лежит на свободной поверхности воды, а основание параллельно ей.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
