Теорема 10. Пусть определена и непрерывна по при и в и, кроме того, имеет для указанных значений непрерывную по обеим переменным производную .

Если интеграл 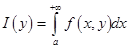сходится для всех 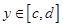, а интеграл 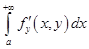сходится равномерно относительно 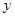в том же промежутке, то 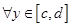имеет место формула .

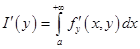► При 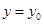рассмотрим 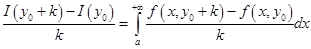и докажем, что здесь допустим предельный переход по параметру 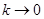под знаком интеграла.

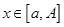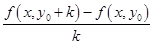Лемма. Если , то при 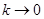стремится к 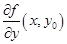равномерно относительно .

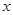► Действительно, из условия непрерывности функции 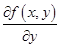на компактном множестве 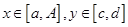следует её равномерная непрерывность на этом множестве, т.е. для любого 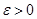существует 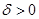такое, что из условий 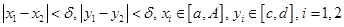следует .

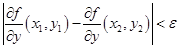При 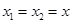, , 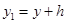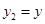из этого неравенства следует, что если 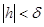, то

.

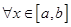
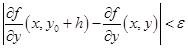Тем самым лемма доказана. ◄

Так как по теореме Лагранжа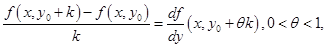

в котором из неравенства 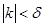следует, что 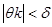и, по доказанному неравенству (1),

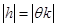
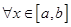получаем: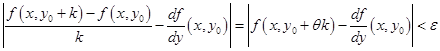

Вернёмся к доказательству теоремы и используем доказанную теорему:

Пусть интегрируема (в собственном смысле) на в промежутке при любом и в каждом таком промежутке при равномерно относительно стремится к предельной функции . Если, кроме того, интеграл сходится равномерно относительно (в ), то .

Чтобы её применить, осталось убедиться в равномерной сходимости относительно 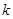интеграла

.

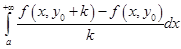По условию, 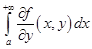сходится равномерно. Это означает, что для любого 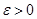существует 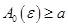такое, что для любых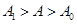

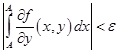(1)

для всех .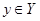

Докажем, что одновременно

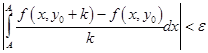(2)

для всех возможных .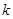

Для этого зафиксируем 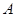и 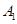и рассмотрим

.

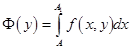Это – собственный интеграл, зависящий от параметра, и к нему применима теорема Лейбница: если 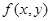непрерывна на 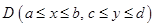, 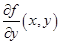тоже непрерывна на 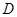, то 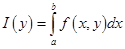дифференцируема на 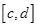, причём 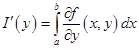(в концах отрезка имеем односторонние производные).

Поэтому .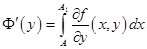

Доказанное выше неравенство (1) означает, что 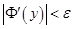для любого .

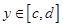Рассмотрим отношение .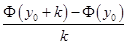

С одной стороны, по теореме Лагранжа эта величина равна .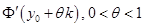

С другой стороны,

.

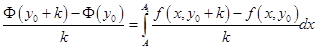Вспомним критерий Коши равномерной сходимости интеграла:

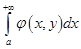равномерно сходится на множестве 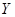тогда и только тогда, когда .

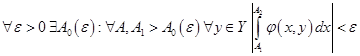Нами доказано, что

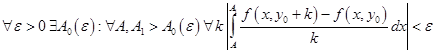
Это означает, что критерий Коши выполняется и что интеграл

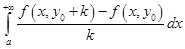
сходится равномерно относительно 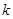. Применяем теорему 21.1 о предельном переходе:

◄

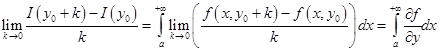ИНТЕГРИРОВАНИЕ НЕСОБСТВЕННОГО ИНТЕГРАЛА ПО ПАРАМЕТРУ

Теорема 11. Пусть непрерывна на множестве , . Если интеграл сходится равномерно на (относительно ), то

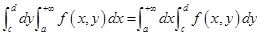(1)

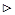Интеграл в левой части существует, т.к. по доказанному выше, 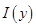- непрерывная функция. По теореме об интегрировании по параметру собственного интеграла, для любого 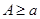имеем:

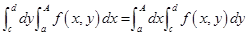(2)

Функция 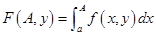непрерывна по 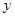(как собственный интеграл от непрерывной функции). Кроме того, 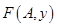стремится к 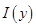при 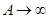равномерно относительно 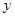(по условию теоремы).

Вспомним доказанную ранее теорему: