Метод наименьших квадратов.
По точкам, полученным в некотором эксперименте, требуется провести прямую линию таким образом, чтобы сумма квадратов отклонений экспериментальных точек от предполагаемой прямой была наименьшей.
у=Ах+В – искомая функция;
А,В – искомые коэффициенты.
Функция 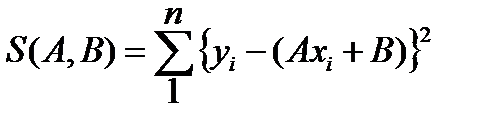 должна достигать минимума при выбранных А,В.
должна достигать минимума при выбранных А,В.
Исследуйте функцию S(A,B) на локальный экстремум.
Получите выражение для А, В, соответствующие экстремуму.
Постройте по методу наименьших квадратов прямую по точкам:
| Хi | Уi |
Контрольные вопросы 1.Дайте определение частной производной первого порядка и производной по направлению. Какова взаимосвязь между ними? 2. Дайте определение градиента скалярного поля. Какова взаимосвязь между градиентом и производной по направлению? 3. Найдите направление наибыстрейшего возрастания функции 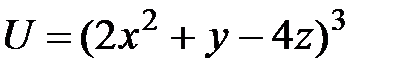 в точке в точке 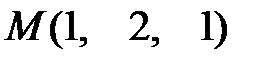 . Какова скорость изменения функции в этом направлении? 4. Запишите общее выражение для дифференциала первого порядка функции двух и трех переменных 5. Найдите смешанные производные для функции . Какова скорость изменения функции в этом направлении? 4. Запишите общее выражение для дифференциала первого порядка функции двух и трех переменных 5. Найдите смешанные производные для функции 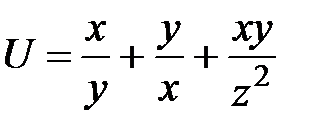 . 6. Частная производная функции . 6. Частная производная функции 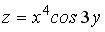 по переменной по переменной 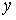 в точке в точке 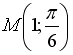 равна… 7. Частная производная функции равна… 7. Частная производная функции 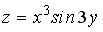 по переменной по переменной 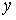 в точке в точке 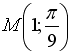 равна… 8. Частная производная функции равна… 8. Частная производная функции 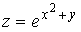 по переменной по переменной 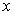 в точке в точке 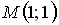 равна… 9. Линиями уровня функции равна… 9. Линиями уровня функции 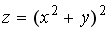 являются … Ответы: Задача 2. а) (-1;1) – максимум; (1;-1) – минимум; б) (-3;2;-1) – максимум; в) (2; -6; 1) – минимум; являются … Ответы: Задача 2. а) (-1;1) – максимум; (1;-1) – минимум; б) (-3;2;-1) – максимум; в) (2; -6; 1) – минимум; |
| Задача 3. Х¹0; l=-1; М1(2;0;-1); М2(-2;0;-1); d2L<0; |
| Задача 4 и примечания к ней У=0,8Х–0,4; |
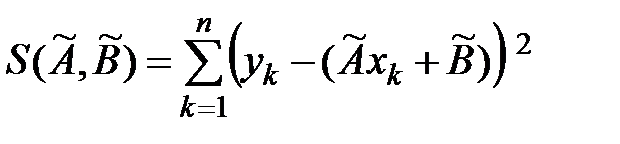 принимает наименьшее значение. Записываем необходимые условия существования экстремума для функции двух переменных принимает наименьшее значение. Записываем необходимые условия существования экстремума для функции двух переменных 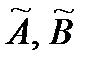 , приравнивая к нулю частные производные: , приравнивая к нулю частные производные: 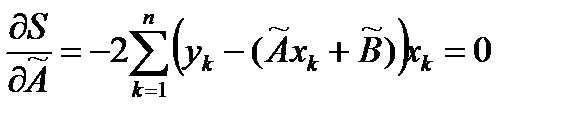 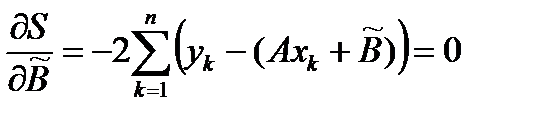 . В результате для нахождения оценок получаем систему уравнений: . В результате для нахождения оценок получаем систему уравнений: 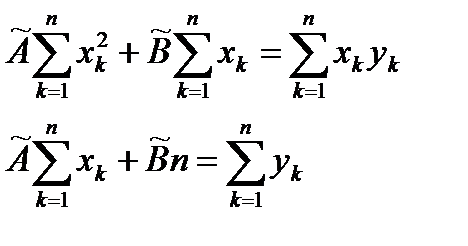 , решение которой имеет вид : , решение которой имеет вид : 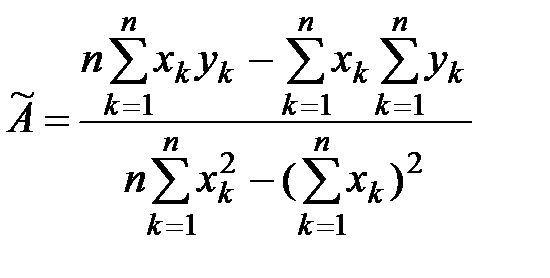 , , 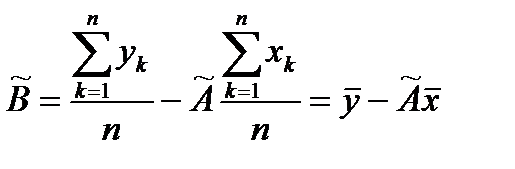 . . |
| Уi | ||
| 10. | ||
Основная учебная литература
Шипачев, В. С. Высшая математика: учебник для вузов [текст] / В. С. Шипачев. – М.: Высш. школа, 2007. – 343 с.
Алексеев Д. В. Конспекты по общему курсу математики: учеб. пособие для студентов инженерно-технических специальностей [электронный ресурс] / Д.В. Алексеев; ГУ КузГТУ. –Кемерово, 2008.
3. Казунина, Г.А. Математика: элементы теории функций комплексного переменного: учеб. пособие для вузов [текст] / Г.А. Казунина, Г.А. Липина, Л.В. Пинчина; ГУ КузГТУ. –Кемерово, 2003. – 104 с.
4. Казунина, Г.А. Преобразования Фурье. Преобразования Лапласа: учеб. пособие для вузов [электронный ресурс] / Г.А. Казунина; ГУ КузГТУ. – Кемерово, 2009.
5. Гмурман, В. Е. Теория вероятностей и математическая статистика: учеб. пособие для вузов [текст] / В. Е. Гмурман. – М.: Высшее образование, 2008. – 479 с.
7.2. Дополнительная учебная литература, книги издательства «Лань»
Берман, Г. Н. Сборник задач по курсу математического анализа: учеб. пособие для вузов [текст] / Г.Н. Берман. – СПб.: Профессия, 2005. – 423 с.
