Признаки сходимости знакопеременных и

ЧИСЛОВЫЕ РЯДЫ

Методические указания к практическим занятиям

по дисциплине «Высшая математика»

Составители: Егорова Ю.Б.

Мамонов И.М.

Корниенко Л.И.

МОСКВА 2005

ВВЕДЕНИЕ

Методические указания предназначены для студентов дневного и вечернего отделения факультета № 14 специальностей 071000, 130200, 220200.

ОСНОВНЫЕ ПОНЯТИЯ

Пусть u₁, u₂, u₃, …, u_n, … - бесконечная числовая последовательность. Выражение 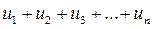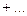называется бесконечным числовым рядом, числа u₁, u₂, u₃, …, u_n - членами ряда; 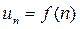называется общим членом ряда. Ряд часто записывают в сокращенном (свернутом) виде: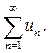

Сумму первых n членов числового ряда обозначают через 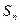и называют n-й частичной суммой ряда:

.

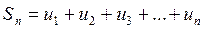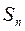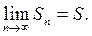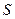Ряд называется сходящимся, если его n-я частичная сумма при неограниченном возрастании n стремится к конечному пределу, т.е. если Число называют суммой ряда.

Если же n-я частичная сумма ряда при 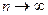не стремится к конечному пределу, то ряд называют расходящимся.

Пример 1.Найти сумму ряда .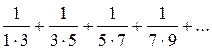

Решение. Имеем 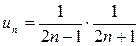. Так как:

,

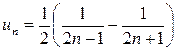то

.

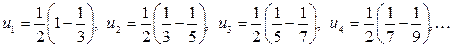Следовательно,

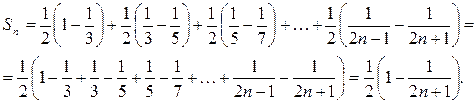
Так как 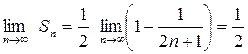, то ряд сходится и его сумма равна .

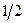ОСНОВНЫЕ ТЕОРЕМЫ О ЧИСЛОВЫХ РЯДАХ

Теорема 1. Если сходится ряд 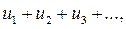то сходится и ряд 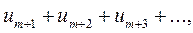получаемый из данного ряда отбрасыванием первых 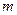членов (этот последний ряд называют 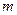-м остатком исходного ряда). И наоборот, из сходимости 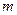-го остатка ряда вытекает сходимость данного ряда.

Теорема 2. Если сходится ряд 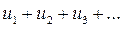и суммой его является число 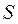, то сходится и ряд 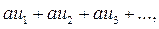причем сумма последнего ряда равна .

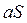Теорема 3. Если сходятся ряды 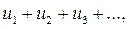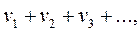имеющие соответственно суммы S и Q, то сходится и ряд 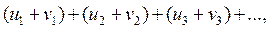причем сумма последнего ряда равна .

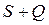Теорема 4 (Необходимый признак сходимости ряда). Если ряд 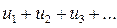сходится, то 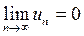, т.е. при 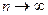предел общего члена сходящегося ряда равен нулю.

Следствие 1. Если 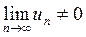, то ряд расходится.

Следствие 2. Если 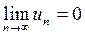, то определить сходимость или расходимость ряда с помощью необходимого признака сходимости нельзя. Ряд может как сходящимся, так и расходящимся.

Пример 2.Исследовать сходимость ряда:

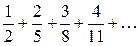
Решение. Находим общий член ряда 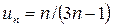. Так как:

,

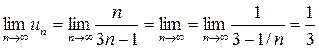т.е. 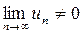, то ряд расходится (не выполняется необходимое условие сходимости).

ПРИЗНАКИ СХОДИМОСТИ РЯДОВ С ПОЛОЖИТЕЛЬНЫМИ

ЧЛЕНАМИ

ПРИЗНАКИ СРАВНЕНИЯ

Признаки сравнения основаны на сравнении сходимости заданного ряда с рядом, сходимость или расходимость которого известна. Для сравнения используются ниже перечисленные ряды.

Ряд 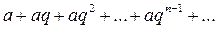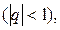составленный из членов любой убывающей геометрической прогрессии, является сходящимся и имеет сумму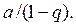

Ряд 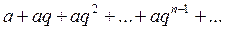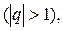составленный из членов возрастающей геометрической прогрессии, является расходящимся.

Ряд 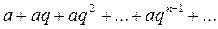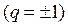является расходящимся.

Ряд 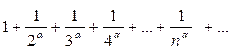называется рядом Дирихле. При a>1 ряд Дирихле сходится, при a<1- расходится.

При a=1 ряд 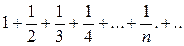называется гармоническим. Гармонический ряд расходится.

Теорема. Первый признак сравнения. Пусть даны два ряда с положительными членами:

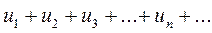(1)

и

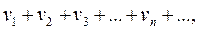
(2)

причем каждый член ряда (1) не превосходит соответствующего члена ряда (2), т.е. 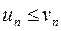(n= 1, 2, 3, …). Тогда если сходится ряд (2), то сходится и ряд (1); если расходится ряд (1), то расходится и ряд (2).

Замечание. Этот признак остается в силе, если неравенствo 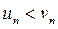выполняется не при всех 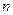, а лишь начиная с некоторого номера n=N, т.е. для всех n³N.

Пример 3.Исследовать сходимость ряда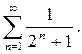

Решение.Члены данного ряда меньше соответствующих членов ряда 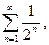составленного из членов бесконечно убывающей геометрической прогрессии. Так как этот ряд сходится, то сходится и заданный ряд.

Теорема. Второй признак сравнения (предельная форма признака сравнения). Если существует конечный и отличный от нуля предел 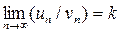, то оба ряда 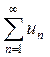и 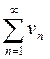одновременно сходятся или расходятся.

Пример 4. Исследовать сходимость ряда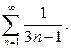

Решение.Сравним ряд с гармоническим рядом 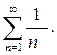Найдем предел отношения общих членов рядов:

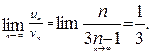
Так как гармонический ряд расходится, то расходится и заданный ряд.

РАДИКАЛЬНЫЙ ПРИЗНАК КОШИ

Теорема.Если для ряда 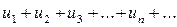существует 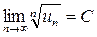, то этот ряд сходится при 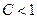и расходится при .

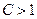Замечание. Если С=1, то вопрос о сходимости остается открытым.

Пример 5. Исследовать сходимость ряда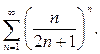

Решение.Применим признак Коши. Найдем предел:

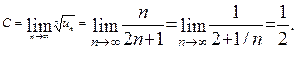
Так как С=1/2<1, то ряд сходится.

ПРИЗНАК ДАЛАМБЕРА

Теорема. Если для ряда 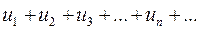существует 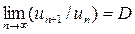, то этот ряд сходится при 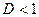и расходится при .

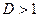Замечание. Если С=1, то вопрос о сходимости остается открытым.

Пример 6. Исследовать сходимость ряда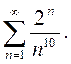

Решение. Применим признак Даламбера. Имеем: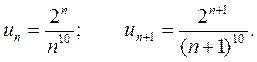

Найдем предел: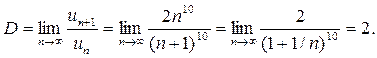

Так как D>1, то ряд расходится.

ИНТЕГРАЛЬНЫЙ ПРИЗНАК КОШИ

Теорема. Есл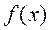и при 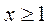- непрерывная, положительная и монотонно убывающая функция, то ряд 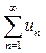, где 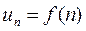, сходится или расходится в зависимости от того, сходится или расходится интеграл .

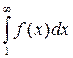Пример 7. Исследовать сходимость ряда, составленного из обратных квадратов: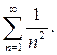

Решение. Имеем: 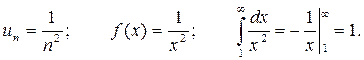Интеграл сходится (является конечной величиной), поэтому сходится и данный ряд.

ПРИЗНАКИ СХОДИМОСТИ ЗНАКОПЕРЕМЕННЫХ И

ЗНАКОЧЕРЕДУЮЩИХСЯ РЯДОВ

Знакопеременные ряды – это ряды как с положительными, так и с отрицательными членами. К знакопеременным рядам относятся знакочередующиеся ряды и ряды с произвольным чередованием знаков своих членов.

Теорема. Достаточный признак абсолютной сходимости знакопеременного ряда. Знакопеременный ряд 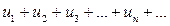сходится, если сходится ряд .

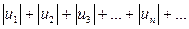В этом случае исходный ряд 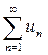называется абсолютно сходящимся.

Сходящийся ряд 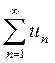называется условно сходящимся, если ряд 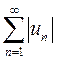расходится.

Если ряд 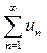абсолютно сходится, то ряд, полученный после любой перестановки бесконечного множества его членов, абсолютно сходится и имеет ту же сумму, что и первоначальный ряд. Если ряд 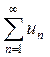условно сходится, то при перестановке бесконечного множества его членов сумма ряда может измениться. В частности, при соответствующей перестановке членов условно сходящегося ряда его можно превратить в расходящийся ряд.

Знакочередующимся рядом называется ряд вида: 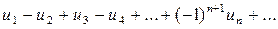, где 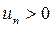(n= 1, 2, 3, …).

Теорема Лейбница. Признак сходимости знакочередующегося ряда. Знакочередующийся ряд сходится, если абсолютные величины его членов убывают, а общий член стремится к нулю, т.е. если выполняются следующие условия: 1) 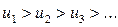и 2) .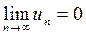

Ряд, удовлетворяющий этим условиям, называется рядом Лейбница.

Возьмем 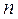-ю частичную сумму ряда Лейбница:

.

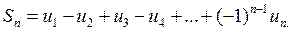Пусть 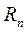- -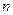й остаток ряда. Его можно записать как разность между суммой ряда S и n-й частичной суммой 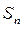, т.е. 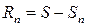или:

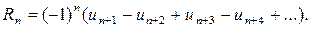
Остаток ряда Лейбница имеет знак своего первого члена и меньше его по абсолютной величине: 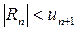. Это неравенство удобно использовать для оценки погрешности, получаемой при замене суммы S ряда Лейбница ее приближенным значением S@ S_n.

Пример 8. Исследовать сходимость знакочередующегося ряда:

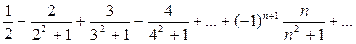
Решение. Применим признак Лейбница:

1) 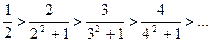Первое условие выполняется.

2) 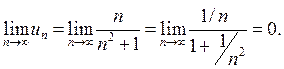Второе условие выполняется.

Следовательно, ряд сходится.

Пример 9. Исследовать сходимость знакочередующегося ряда:

1,1-1,01+1,001-1,0001+…+(-1)ⁿ⁺¹(1+10^-n)+…

Решение. Применим признак Лейбница:

1) 1,1>1,01>1,001>1,0001>… Первое условие выполняется.

2) 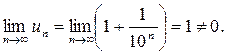Второе необходимое условие сходимости ряда не выполняется. Следовательно, ряд расходится.

Пример 10. Исследовать сходимость знакочередующегося ряда:

1 - 1+1 - 1+…+(-1)ⁿ⁺¹+…

Решение. Общий член ряда не стремится к нулю, поэтому ряд расходится.

Пример 11. Исследовать сходимость знакопеременного ряда: .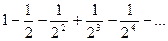

Решение. Составим ряд из абсолютных величин: 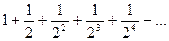Этот ряд составлен из членов убывающей геометрической прогрессии и, следовательно, сходится. Значит, и данный ряд сходится, причем абсолютно.

Пример 12. Исследовать на абсолютную сходимость ряд:

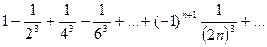
Найти приближенно (с точностью 0,01) сумму этого ряда.

Решение. Так как ряд знакочередующийся, то можно применить теорему Лейбница. Все условия теоремы Лейбница выполнены:

1)

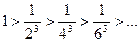
2)

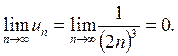
Следовательно, ряд сходится. Причем этот ряд сходится абсолютно, так как сходится ряд из абсолютных величин членов данного ряда:

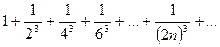
Сходимость этого последнего ряда легко обнаружить, если применить признаки сравнения или интегральный признак Коши.

Применим интегральный признак:

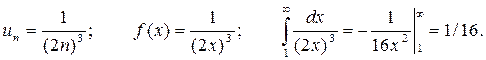
Интеграл сходится (является конечной величиной), поэтому сходится ряд, составленный из абсолютных величин знакочередующегося ряда. Следовательно, знакочередующийся ряд сходится абсолютно.

Для того чтобы найти сумму заданного ряда с точностью 0,01, надо взять столько его членов, чтобы следующий член ряда был по модулю меньше 0,01. Для данного ряда модуль четвертого члена 1/6³=1/216<0,01, поэтому с точностью 0,01:

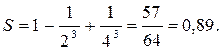
КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дайте определение числового ряда. Какие ряды называются сходящимися и расходящимися?

2. Перечислите основные свойства числовых рядов.

3. Назовите признаки сходимости рядов с положительными членами.

4. Дайте определения знакочередующихся и знакопеременных рядов.

5. Сформулируйте признак Лейбница.

6. Дайте определения абсолютно и условно сходящихся знакопеременных рядов.

7. Сформулируйте достаточный признак абсолютной сходимости знакопеременного ряда.

8. Как можно оценить сумму знакочередующегося ряда с заданной точностью?

ЛИТЕРАТУРА

1. Мантуров О.В. Курс высшей математики. – М.: Высш. шк., 1991. - 448 с.

2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 2. - М.: Высш. шк., 1980. - 365 с.

3. Пискунов Н.С. Дифференциальное и интегральное исчисления. Т. 2 – М.: Наука, 1972. - 312 с.

4. Задачи и упражнения по математическому анализу для втузов. /Под ред. Б.П. Демидовича. – М.: Высш. шк., 1972. - 472 с.

5. Сборник задач по курсу высшей математики. /Под ред. Г.И.Кручковича. - М.: Высш. шк., 1973. - 576 с.

6. Берман А.Ф., Араманович И.Г. Краткий курс математического анализа для вузов. – М.: Наука, 1989. - 736 с.

ОГЛАВЛЕНИЕ

Введение…………………………………………………………………………..3

1. Основные понятия…………….………………………………………..……...3

2. Основные теоремы о числовых рядах ..……………………………………..4

3. Признаки сходимости рядов с положительными членами …………………5

4. Признаки сходимости знакопеременных и знакочередующихся рядов…...9

5. Контрольные вопросы………………………………………………………...12

Литература……….………………………………………………………………. 13