Общая задача линейного программирования

Введение

Линейные модели являются одним из наиболее активно используемых классов математических моделей. Они сравнительно просты, хорошо разработаны, допускают полное исследование и достаточно эффективны в целом ряде стандартных ситуаций.

Линейное программирование – это математический метод решения задачи оптимального распределения имеющихся ресурсов (денег, материалов, времени) для достижения определённой цели (наибольшего дохода или наименьших издержек). Программирование в данном термине имеет смысл планирования. Линейное означает, что ищется экстремум линейной целевой функции при линейных ограничениях (линейных уравнениях или линейных неравенствах).

Общие ситуации, в которых линейное программирование применяется часто и эффективно:

задачи о составлении смеси, цель которых заключается в выборе наиболее экономичной смеси ингредиентов (руды, нефти, пищевых продуктов и др.) при учёте ограничений на физический или химический состав смеси и на наличие необходимых материалов;

задачи производства, целью которых является подбор наиболее выгодной производственной программы выпуска одного или нескольких видов продукции при использовании некоторого числа ограниченных источников сырья;

задачи распределения, цель которых состоит в том, чтобы организовать доставку материалов от некоторого числа источников к некоторому числу потребителей так, чтобы оказались минимальными либо расходы по этой доставке, либо время затрачиваемое на неё, либо некоторая комбинация того и другого. В простейшем виде это задача о перевозках (транспортная задача).

Наиболее распространённым методом решения задачи линейного программирования является симплекс-метод. В простейшем случае, когда число переменных равно двум, удобен простой и наглядный графический метод.

Общая задача линейного программирования

Задача линейного программирования состоит в составлении плана максимизирующего или минимизирующего некую линейную функцию при ограничениях в виде линейных уравнений или линейных неравенств:

найти вектор 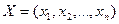, максимизирующий (минимизирующий) функцию

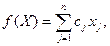(1)

и удовлетворяющий условиям

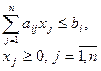(2)

Линейная функция 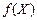называется целевой функцией задачи. Условия (2) называются ограничениями задачи.

Любое решение системы ограничений ЗЛП называется допустимымпланом.

Допустимый план, максимизирующий или минимизирующий целевую функцию называется оптимальным.

План, у которого отличным от нуля компонентам соответствует система линейно независимых векторов, называется опорным планом.

Теорема. Множество планов задачи линейного программирования является выпуклым множеством.

Теорема. Оптимальный план задачи линейного программирования находится в крайней точке выпуклого множества планов. Если оптимальный план находится в двух крайних точках выпуклого множества планов, то он находится также и в любой точке, являющейся выпуклой комбинацией этих крайних точек.

Формы ЗЛП

Форма задачи линейного программирования, у которой ограничения заданы в виде неравенств, называется стандартной, а форма задачи, у которой ограничения заданы в виде уравнений – канонической. Если же система ограничений содержит и уравнения и неравенства, то такая форма называется смешанной.

Стандартная	Каноническая	Смешанная
		, ,
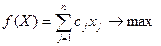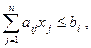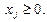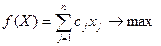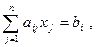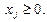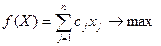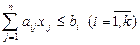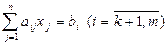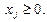