Математическое описание звена. Апериодическое звено II-ого порядка

ЛЕКЦИЯ 4.

Апериодическое звено II-ого порядка

Передаточная функция.

Передаточная функция апериодического звена II-ого порядка имеет вид:

W(s) = K/[(T₁·s + 1)·(T₂·s + 1)]

где K – коэффициент усиления; T₁ и T₂ – постоянные времени, также характеризующая инерционность системы, т.е. продолжительность переходного процесса в ней. (T₁ > 0 и T₂ > 0).

Математическое описание звена.

Апериодическое звено II-ого порядка описывается дифференциальным уравнением второго порядка:

(T₁T₂)·d²у(t)/dt² + (T₁ + T₂)·dу(t)/dt + у(t) = K·х(t)

Физическая реализация звена.

Апериодическое звено II-ого порядка можно рассматривать как комбинацию двух апериодических звеньев I-ого порядка, т.е. это могут быть различного рода двухъемкостные (двухкаскадные) тепловые, гидравлические и пневматические объекты. Примером апериодического звена II-ого порядка также является двухфазный асинхронный электродвигатель.

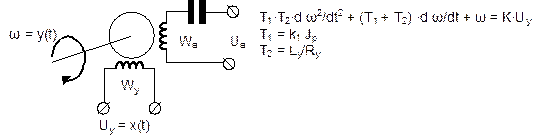
Переходная характеристика.

Переходная характеристика апериодического звена II-ого порядка имеет вид:

h(t) = L^-1[W(s)·1(t)] = L^-1[K/[s·(T₁·s + 1)·(T₂·s + 1)]] =

= K·[1 – (T₁/(T₁ – T₂))·e^-t/T1 – (T₂/(T₂ – T₁))·e^-t/T2]

В частном случае, когда T₁ = T₂ = T аналитическое выражение для переходной характеристики имеет несколько иной вид:

h(t) = L^-1[W(s)·1(t)] = L^-1[K/[s·(T·s + 1)²]] =

= K·[1 – e^-t/T – (t/T)·e^-t/T]

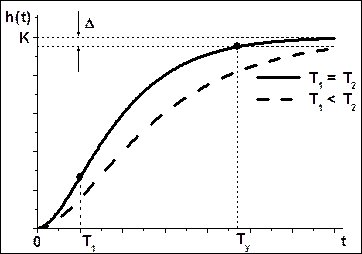
Рис. 4.1. Переходная характеристика апериодического звена П-го порядка.

Переходный процесс апериодического звена II-ого порядка имеет экспоненциальный вид с перегибом в начальной области. Это означает, что звено имеет высокую инерционность и как бы не сразу начинает реагировать на входное воздействие. Установившееся значение равно: h_уст = K.

Время регулирования T_у (время переходного процесса) для апериодического звена II-ого порядка в 3 – 5 раз превышает значение большей из постоянных времени.

T_у ≈ (3 ÷ 5)·T₂

Весовая функция.

Весовая функция апериодического звена II-ого порядка имеет вид:

w(t) = L^-1[W(s)] = L^-1[K/ [(T₁·s + 1)·(T₂·s + 1)]] =

= K·[(1/(T₁ – T₂))·e^-t/T1 + (1/(T₂ – T₁))·e^-t/T2]

В частном случае, когда T₁ = T₂ = T аналитическое выражение для весовой функции имеет несколько иной вид:

w(t) = L^-1[W(s)] = L^-1[K/ (T₁·s + 1)²] =

= (K·t/T²)·e^-t/T

Для весовой функции апериодического звена II-ого порядка характерно плавное изменение амплитуды с максимумом: 1) в точке t = T для случая, когда T₁ = T₂ = T; 2) в точке t = T_П (приведенная постоянная времени) для случая, когда T₁ ≠ T₂.

Приведенная постоянная времени T_п определяется по формуле:

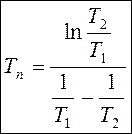
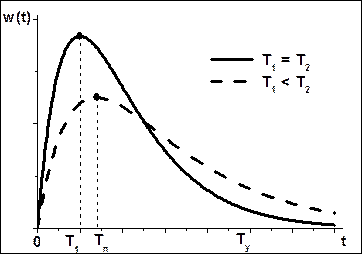
Рис. 4.2. Весовая характеристика апериодического звена П-го порядка.

Частотные характеристики.

Частотные характеристики (АФЧХ, АЧХ, ФЧХ и ЛАХ) апериодического звена II-ого порядка имеют достаточно сложный аналитический вид.

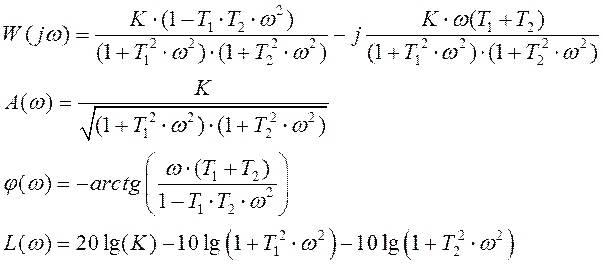
Переход к асимптотической ЛАХ: Будем считать, что T₁ > T₂. Аналогично случаю апериодического звена I-ого порядка вводим сопрягающие частоты w₁ = 1/T₁ и w₂ = 1/T₂, которые делят весь частотный диапазон на три участка: область низких частот, область высоких частот и промежуточную область.

Область низких частот: w << w₁; можно пренебречь выражениями под логарифмами. Получаем: L(w) = 20lgK. Это горизонтальная прямая.

Область высоких частот: w >>w₂; в логарифмах можно пренебречь единицами. Получаем L(w) = 20lgK – 20lgT₁w – 20lgT₂w. Это – уравнение прямой с наклоном -40дб/декаду.

Промежуточная область частот: w₁ > w > w₂. Строим прямую, соединяющую оба предыдущих участка.. Получаем L(w) = 20lgK – 20lgT₁w. Это – уравнение прямой с наклоном -20дб/декаду.

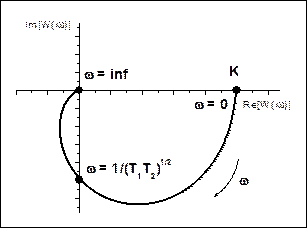
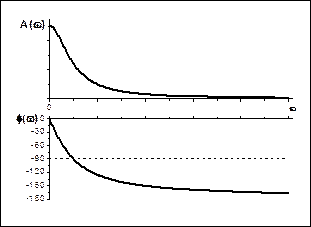
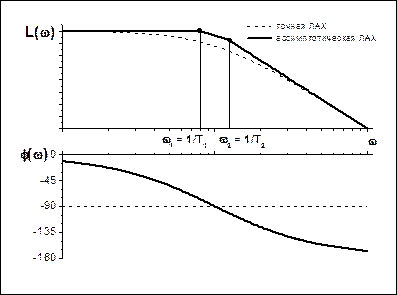
Рис. 4.3. АФЧХ, АЧХ, ФЧХ, ЛАХ и ЛФХ апериодического звена II-ого порядка.

Колебательное звено

Передаточная функция.

Передаточная функция колебательного звена имеет вид:

W(s) = K/[T²·s² + 2T·ξ·s + 1]

где K – коэффициент передачи; T – постоянная времени, характеризующая инерционность системы, т.е. продолжительность переходного процесса в ней. (T > 0); ξ – коэффициент (декремент) затухания, который характеризует рассеяние энергии в звене ( 0 < ξ < 1).

При ξ 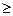1 колебательное звено превращается в апериодическое звено П-го порядка.

Математическое описание звена.

Колебательное звено описывается дифференциальным уравнением второго порядка:

T²·d²у(t)/dt² + 2T ξ·dу(t)/dt + у(t) = K·х(t)