Экспериментальная проверка метода наложения

Проверку метода наложения, согласно которого, токи в разветвлённых электрических цепях определяются как алгебраическая сумма токов от каждого источника в отдельности, осуществляем с помощью электрической цепи рассмотренной в примере 2.15 и приведенной на рисунке 2.121.

Для измерения частичных токов от действия источника напряжения 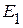, используем электрическую схему, приведенную на рисунке 2.122 а, в которой удален источник напряжения 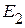. Для измерения частичных токов от действия источника напряжения 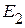, используем электрическую схему, приведенную на рисунке 2.122 б.

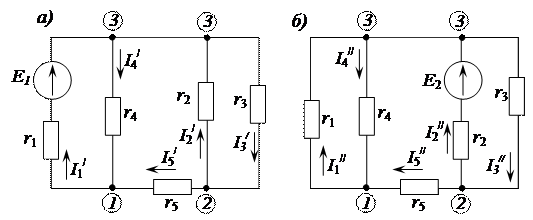
Рисунок 2.122 – Схема для определения частичных токов

В таблице 13 приведены экспериментальные значения частичных токов при различных режимах цепи.

Таблица 13 – Значения частичных токов

Режимы цепи	I1,мА	I2,мА	I3,мА	I4,мА	I5,мА
В схеме включены два источника Е1 и Е2	93,9	24,1	41,4	76,3	17,5
В схеме включен только источник Е1	126,8	-44,4	14,9	67,2	58,2
В схеме включен только источник Е2	-32,2	67,9	25,9	8,2	-41,8
Алгебраическая сумма частичных токов	94,6	23,5	40,8	75,4	16,4

Из сравнения результатов расчета алгебраической суммы частичных токов и результатов эксперимента, от действия двух источников питания, следует их практическая сходимость, что подтверждает справедливость метода наложения.

Необходимо отметить, что результаты измерения частичных токов, приведенные в таблице 13, подтверждены и расчетным путем, приведенным в примере 2.15.

Экспериментальная проверка метода

Эквивалентного генератора

Согласно метода эквивалентного генератора, любая сложная линейная цепь по отношению к заданной ветви может быть представлена активным двухполюсником, который может быть представлен эквивалентным источником питания (эквивалентным генератором) с ЭДС 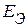и внутренним сопротивлением 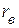. Величина ЭДС эквивалентного генератора равна напряжению холостого хода на зажимах активного двухполюсника 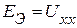, а внутреннее сопротивление равно входному сопротивлению пассивного двухполюсника, полученного из активного – .

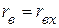Проверку метода эквивалентного генератора рассмотрим на примере определения тока 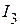, электрической схемы приведенной на рисунке 2.121. Согласно метода эквивалентного генератора, 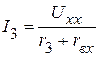. С этой целью, измеряем напряжение холостого хода 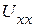активного двухполюсника (рис. 2.123 а). Далее в этой ветви, измеряем ток короткого замыкания 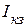(рис. 2.123 б).

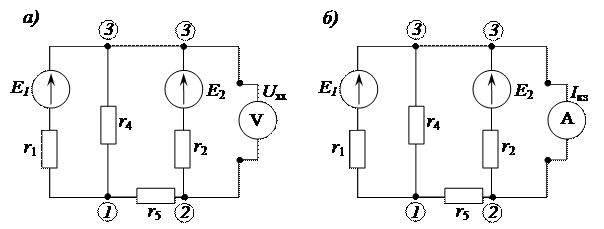
Рисунок 2.123, – Экспериментальные схемы для определения

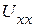и

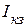
По результатам опытов холостого хода и короткого замыкания, определяем входное сопротивление пассивного двухполюсника, равное по величине .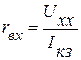

В таблице 14 приведены экспериментальные значения напряжения холостого хода, входного сопротивления и тока в ветви с резистивным сопротивлением .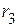

Таблица 14 – Экспериментальные и расчетные значения

	Uхх, В	Iкз, мА	rвх , Ом	I3, мА
эксперимент	15,31		67,74	41,63
расчет	15,34	-	65,51	41,97

В таблице 14 также указаны результаты расчета тока 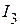, приведенные в примере 2.17.

Сравнения результатов расчета и экспериментов следует значений напряжения холостого хода, входного сопротивления и тока в определяемой ветви, подтверждает справедливость метода эквивалентного генератора.

Входное сопротивление пассивного двухполюсника 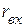, можно измерить омметром. С этой целью из схемы активного двухполюсника удаляем источники питания и заменяем их внутренними сопротивлениями (перемычка). В результате получаем схему пассивного двухполюсника (рис. 2.124), входное сопротивление которой измеряем омметром

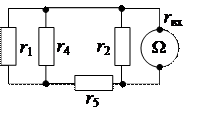
Рисунок 2.124 - Схема пассивного двухполюсника

Входное сопротивление пассивного двухполюсника, определенное с помощью омметра, соответственно равно 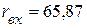Ом.