Постановка задачи оптимизации и метод решения

Оптимальное решение задачи компаундирования бензинов является чрезвычайно важным для результатов работы всего нефтеперерабатывающего предприятия. Согласно технологическому процессу компаундирования, начальная рецептура товарного бензина, рассчитывается по типовым октановым числам компонентов, отклонения которых регламентируются стандартами. Таким образом, октановые числа компонентов, поступающих на смешение, точно не известны, для них известны только интервалы их возможных значений. То есть на практике октановые числа компонентов отличаются от значений, используемых при составлении рецептуры. Значения октановых чисел компонентов, поступающих с технологических установок на смешение, могут также изменяться во времени в зависимости от состояния работы установки.

Таким образом, можно поддерживать точно заданное соотношение компонентов смеси согласно рецептуре, однако на выходе смесителя качество товарного продукта будет отличаться от заданного.

Целью задачи компаундирования является получение товарного бензина требуемого качества при минимизации его стоимости. Стоимость товарного бензина 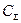определяется стоимо­стью 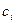и количеством 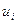каждого из входящих в него компонентов как 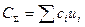. Поэтому цель задачи управления процессом смешения математически можно представить в следующем виде /1/

C^TU 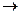min (1)

где 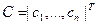- вектор стоимости входящих в товарный бензин компонентов;

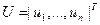- вектор величин потоков смешиваемых компонентов;

n - число смешиваемых компонентов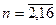

Так как стоимости отдельных компонентов являются на этапе решения задачи (1) определенными величинами, минимизация прово­дится только по векторуU.

На управляющие воздействия 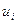накладываются естественные ограничения, связанные с физическим смыслом этих величин

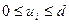(2)

где i = 1, ..., n,

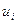- компоненты вектора U ,

d - известная величина, равная максимальной пропускной способности трубопроводов, по кото­рым поступают компоненты смеси (предполагается, что все эти трубо­проводы одинаковы).

Требованиями устойчивости процесса смешивания вызвана необхо­димость соблюдения следующих ограничений

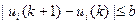
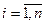(3)

где k - моменты дискретного времени k = 0,1. ... ;

запись u_i(k) обозначает зависимость величины u_i от конкретного момента времени;

b - известная величина, задаваемая оператором-технологом.

Технологические требования к содержанию количества смеси в тру­бопроводе с конечным продуктом определяют ограничение, физический смысл которого состоит в неизменности величины потока товарного бензина

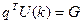(4)

где q - вектор размерности n , все компоненты которого равны единице;

G - заранее заданная величина, которая устанавливается

оператором-технологом.

Качество товарного бензина нормируется государственными стан­дартами или стандартами предприятия. Среди нормируемых показателей основным является октановое число 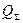товарного бензина. Требования, предъявляемые к величине 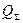могут быть записаны в виде,

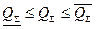, (5)

где 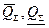- соответственно верхняя и нижняя допустимые грани­цы октанового числа товарного бензина, получаемого в результате смешивания всех компонент в потоке.

Известно, что чем ниже октановое число нефтепродуктов, тем меньше его стоимость. Поэтому желательно, чтобы октановое число получаемого товарного бензина соответствовало нижней допустимой границе интервала (5) , т.е.

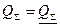(6)

Математическая модель технологического процесса смешивания бензиновых фракций может быть описана следующим векторным уравнением

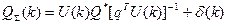(7)

где 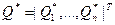вектор октановых чисел компонентов товарного бензина в смешиваемых по­токах;

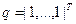- вектор размерности n, все компонен­ты которого равны единице;

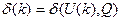- величина, равная второму слагаемому правой части математической модели октанового числа (7.1) и характеризующая степень нелинейности процесса /2/;

k=0,1,… - моменты дискретного времени.

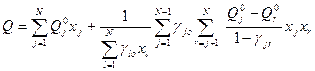(7.1)

Если среди смешиваемых компонент нет антидетонаторов, то октановое число продукта может быть достаточно точно рассчитано, как линейная зависимость от октановых чисел компонентов смеше­ния /2/. Это означает, что величина 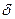, характеризующая нели­нейность процесса, не превышает для рассматриваемых веществ и ин­тервалов изменения их количества некоторой постоянной величины 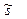, которая может быть установлена экспериментальным путем. Более точ­но величина 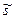определена в /1/.

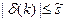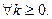, (8)

Решение задачи (1) при ограничениях (2) - (8) может быть получено путем вычисления вектора оптимальных управляющих воздействий методами линейного программирования, например симплекс-метода, если известен вектор октановых чисел 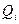компонентов смеси модели (7) .

Однако октановые числа 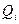, смешиваемых компонентов точно неизвестны, известны лишь их интервальные оценки следующего ви­да

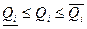(9)

для всех i = 1,2, ... , n.

Поэтому задача оптимизации процесса компаундирования сво­дится к поочередному решению следующих задач:

-идентификации неизвестных параметров Q модели (7);

-решению задачи линейного программирования (1) при ограничениях (2) - (8).