Диференціальне числення функцій однієї змінної.

1) Що називається похідною функції?

2) У чому полягає фізичний зміст похідної?

3) У чому полягає геометричний зміст похідної? Наведіть рів­няння дотичної та нормалі до графіка функції.

4) Який зв’язок між диференційованістю та неперервністю?

5) За якими правилами обчислюється похідна суми, різниці, до­бутку та частки двох функцій?

6) Як знаходиться похідна складеної функції? Оберненої функ­ції? Параметрично заданої функції?

7) Наведіть формули похідних основних елементарних функ­цій.

8) Як здійснюється диференціювання неявно заданої функції?

9) У чому полягає правило логарифмічного диференціювання?

10) Дайте означення похідної 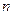-го порядку. У чому полягає фі­зичний зміст другої похідної?

11) Що називається диференціалом функції?

12) У чому полягає геометричний зміст диференціала?

13) Як зв’язані похідна і диференціал?

14) За якими правилами обчислюється диференціал суми, різни­ці, до­бутку та частки двох функцій?

15) Наведіть формули диференціалів основних елементарних функ­цій.

16) Як диференціал застосовується в наближених обчисленнях?

17) Що називається диференціалом 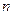-го порядку?

18) У чому полягає інваріантність форми першого диференціа­ла? Чи поширюється властивість інваріантності на диферен­ціали вищих порядків?

19) Сформулюйте теорему Ролля про корені похідної. Який її гео­метричний зміст?

20) Сформулюйте теорему Лагранжа про скінченні прирости. Який її геометричний зміст?

21) Сформулюйте теорему Ко­ші про відношення при­рос­тів двох функцій.

22) У чому полягає правило Лопіталя? Для розкриття невизна­ченостей яких видів воно застосовується безпосередньо?

23) Як зводяться невизначеності , , , і до одного з основних видів чи ?

24) Наведіть формулу Тейлора 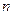-го порядку із залишковим чле­ном у формі Лагранжа.

25) Як записується формула Тейлора в диференціальній формі?

26) Наведіть приклади розкладання функцій за фор­мулою Ма­кло­рена.

27) Як формула Тейлора застосовується в наближених обчис­лен­нях?

28) У чому полягають достатні умови монотонності та сталості функції?

29) Що називається точкою мінімуму функції? Точкою макси­муму?

30) У чому полягає необхідна умова екстремуму?

31) Що таке критичні точки першої похідної? Стаціонарні точки функції?

32) У чому полягає достатня умова екстремуму за першою по­хідною?

33) Сформулюйте правило дослідження функції на монотон­ність і екстремум за першою похідною.

34) У чому полягає достатня умова гладкого екстремуму за дру­гою похідною?

35) Як знаходяться найменше та найбільше значення функції в замкненій області?

36) Яка функція називається опуклою (вгнутою) в точці та на інтервалі?

37) Що таке точка перегину?

38) У чому полягають достатні умови опуклості та вгнутості?

39) У чому полягає необхідна умова точки перегину?

40) Що таке критичні точки другої похідної?

41) Сформулюйте правило дослідження функції на опуклість, угнутість та перегин за другою похідною.

42) Що називається асимптотою графіка функції? На які види діляться асимптоти?

43) Який вигляд має рівняння вертикальної асимптоти? Похилої асимптоти?

44) Опишіть загальну схему повного дослідження функції та по­будови ескіза графіка.