Тема 1. Елементи лінійної алгебри
Лекція 1.1. Матриці. Дії над матрицями. Визначники 2-го, 3-го, та n-го порядку. Властивості визначників. Обернена матриця. Мінор к-го порядку. Ранг матриці
Матриці
Означення.Матрицею розміру т на п називають прямокутну таблицю т  п чисел, що складається з т рядків і п стовпців.
п чисел, що складається з т рядків і п стовпців.
Позначення матриці:
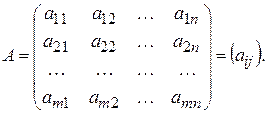
Числа 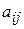 називають елементами матриці, де і – номер рядка, а j – номер стовпця, на перетині яких міститься елемент
називають елементами матриці, де і – номер рядка, а j – номер стовпця, на перетині яких міститься елемент 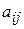 .
.
Матрицю, що складається лише з одного рядка, називають матрицею-рядком і позначають
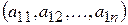 ,
,
а матрицю лише з одним стовпцем – матрицею-стовпцем і позначають
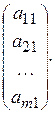
Дві матриці вважаються рівними,якщо в них однакові кількості рядків і стовпців, а також рівні між собою відповідні елементи.
Матрицю, всі елементи якої дорівнюють нулю, називають нульовою і позначають
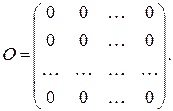
Квадратноюназивають матрицю, в якої кількість рядків дорівнює кількості стовпців, тобто т=п. Її позначають так:
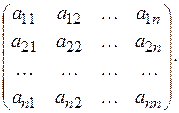
Число п називають порядком матриці.Елементи 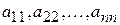 квадратної матриці утворюють її головну діагональ,а елементи
квадратної матриці утворюють її головну діагональ,а елементи 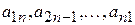 - побічну діагональ.
- побічну діагональ.
Діагональною називають квадратну матрицю, в якої всі елементи, що розміщені не на головній діагоналі, дорівнюють нулю. Її позначають так:
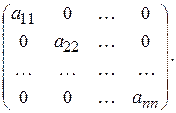
Одиничноюназивають діагональну матрицю, в якої всі елементи головної діагоналі дорівнюють одиниці:
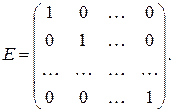
Дії над матрицями
Лінійними операціями над матрицяминазивають операції (дії) додавання, віднімання матриць (лише однакового розміру) та множення їх на число.
Означення. Сумою (різницею) двох матриць 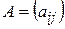 і
і 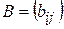 розміру т
розміру т 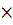 п називають таку матрицю
п називають таку матрицю 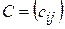 розміру т
розміру т  п, елементи якої визначаються рівністю
п, елементи якої визначаються рівністю 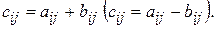 Позначення суми (різниці):
Позначення суми (різниці):
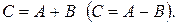
Означення. Добутком матриці 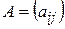 на дійсне число
на дійсне число 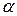 називають матрицю
називають матрицю 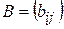 , елементи якої визначаються рівністю
, елементи якої визначаються рівністю 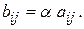 Це записують так:
Це записують так: 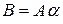 або
або 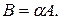
Матрицю 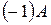 називають протилежноюматриці А і позначають –А.
називають протилежноюматриці А і позначають –А.
В л а с т и в о с т і л і н і й н и х о п е р а ц і й н а д м а т р и ц я м и
j 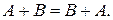 n
n 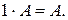
k 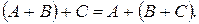 o
o 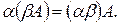
l 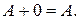 p
p 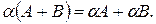
m 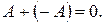 q
q 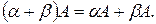
Дія множення матриці на матрицю вводиться лише для узгоджених матриць. Матрицю А називають узгодженою з матрицею В, якщо кількість стовпців матриці А дорівнює кількості рядків матриці В.
Нехай матриця 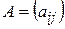 ,
, 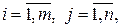 тобто має розмір
тобто має розмір 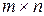 , а матриця
, а матриця 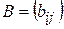 ,
, 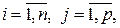 тобто має розмір
тобто має розмір 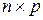 .
.
Означення. Добутком матриці 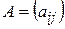 на матрицю
на матрицю 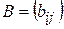 називають матрицю
називають матрицю 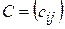 , елементи якої визначаються рівністю
, елементи якої визначаються рівністю 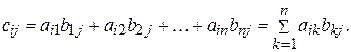
Зауваження. У загальному випадку 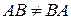 , тобто множення матриць – операція не комутативна. Якщо
, тобто множення матриць – операція не комутативна. Якщо 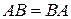 , то матриці А і В називають комутативними.
, то матриці А і В називають комутативними.
В л а с т и в о с т і о п е р а ц і ї м н о ж е н н я м а т р и ц ь
j 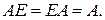 m
m 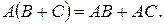
k 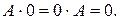 n
n 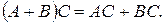
l 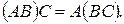 o
o 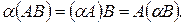
Операція піднесення до степеня визначена тільки для квадратних матриць.
Означення. Цілим додатним степенем 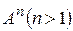 квадратної матриці Аназивають добуток п матриць, рівних А, тобто
квадратної матриці Аназивають добуток п матриць, рівних А, тобто 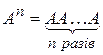 .
.
Для кожної матриці 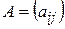 розміру
розміру 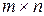 можна побудувати матрицю
можна побудувати матрицю 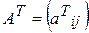 розміру
розміру 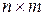 , елементи якої визначаються рівністю
, елементи якої визначаються рівністю 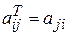 . Матрицю
. Матрицю 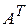 називають транспонованою до матриці А.
називають транспонованою до матриці А.
В л а с т и в о с т і о п е р а ц і ї т р а н с п о н у в а н н я м а т р и ц ь
j 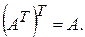 l
l 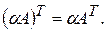
k 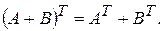 m
m 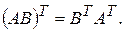
Визначники 2-го, 3-го, та n-го порядку
Означення. Вираз
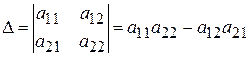 називається визначником другого порядку.
називається визначником другого порядку.
Означення. Вираз
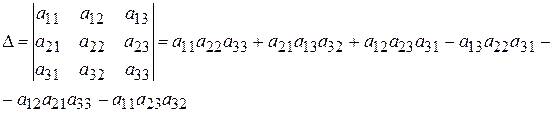 називається визначником третього порядку.
називається визначником третього порядку.
Визначник третього порядку обчислюється за правилом трикутника.














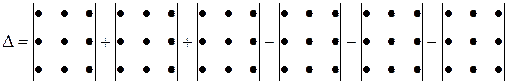
Розглянемо квадратну матрицю А п-го порядку.
Означення. Вираз
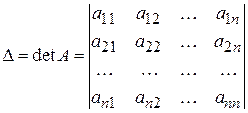 називається визначником п-порядку.
називається визначником п-порядку.
Означення. Мінором 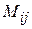 елемента
елемента 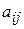 визначника називається визначник, який утворюється з даного визначника в результаті ви креслення і-го рядка та j-го стовпця.
визначника називається визначник, який утворюється з даного визначника в результаті ви креслення і-го рядка та j-го стовпця.
Означення. Алгебраїчним доповненням 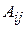 елемента
елемента 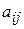 визначника називається мінор, взятий зі знаком
визначника називається мінор, взятий зі знаком 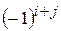 , тобто
, тобто 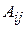 =
= 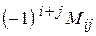 .
.
Теорема 1. Визначник квадратної матриці дорівнює сумі добутків елементів будь-якого рядка (стовпця) на їхні алгебраїчні доповнення:
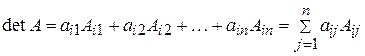
(розклад визначника за елементами і-го рядка; 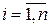 );
);
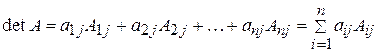
(розклад визначника за елементами j-го рядка; 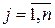 ).
).
Теорема 2. Сума добутків елементів будь-якого рядка (стовпця) визначника на алгебраїчні доповнення відповідних елементів іншого рядка (стовпця)дорівнює нулеві.
В л а с т и в о с т і в и з н а ч н и к і в
j У разі транспонування матриці її визначник не змінюється.
k Якщо всі елементи деякого рядка (стовпця) визначника дорівнюють нулеві, то й визначник дорівнює нулеві.
l У разі переставлення двох рядків (стовпців) визначник змінює знак на протилежний.
m Спільний множник усіх елементів деякого рядка (стовпця) визначника можна виносити за знак визначника.
n Визначник, який має два пропорційних рядки (стовпці), дорівнює нулеві.
o Якщо і-й рядок (стовпець) матриці С дорівнює сумі і-го рядка (стовпця) матриці А та і-го рядка (стовпця) матриці В, а всі інші рядки (стовпці) матриць А, В, С відповідно дорівнюють один одному, то
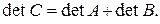
p Визначник не зміниться, якщо до елементів його одного рядка (стовпця) додати відповідні елементи іншого рядка (стовпця), помножені на довільне число.
q Визначник добутку матриць дорівнює добуткові визначників цих матриць.
Обернена матриця
Означення. Оберненою матрицею до квадратної матриці А називають таку матрицю 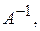 для якої
для якої 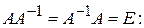
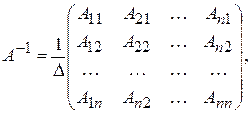
де 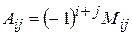 - алгебраїчне доповнення елемента
- алгебраїчне доповнення елемента 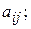
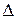 - визначник матриці А.
- визначник матриці А.
Означення. Квадратну матрицю називають невиродженою,або неособливою,якщо її визначник не дорівнює нулю ( 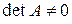 ); у протилежному разі (
); у протилежному разі ( 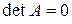 ) матрицю називають виродженою, або особливою.
) матрицю називають виродженою, або особливою.
Теорема 3. Кожна неособлива матриця А має обернену, і до того ж тільки одну.
В л а с т и в о с т і о б е р н е н и х м а т р и ц ь
1. Оберненою до матриці 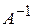 є матриця
є матриця 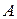 :
: 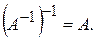
2. Обернена матриця до добутку двох матриць дорівнює добутку обернених матриць до матриць співмножників, взятих у зворотному порядку: 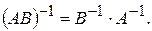
3. Обернена матриця до транспонованої матриці дорівнює матриці, транспонованій до оберненої: 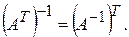
Мінор к-го порядку. Ранг матриці
Нехай задано матрицю 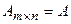 . Виділимо в матриці А будь-які k рядків і стільки ж стовпців, де k – число не більше чисел m і n, тобто
. Виділимо в матриці А будь-які k рядків і стільки ж стовпців, де k – число не більше чисел m і n, тобто 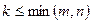 .
.
Визначник порядку k, складений з елементів, що стоять на перетині виділених рядків і стовпців, називається міноромk-го порядку матриці А.
Рангом матриці називається найбільший порядок відмінного від нуля мінора матриці і позначається 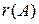 . Ранг нульової матриці дорівнює нулеві.
. Ранг нульової матриці дорівнює нулеві.
Елементарні перетворення матриці:
1. множення деякого рядка (стовпця) матриці на відмінне від нуля число;
2. додавання до деякого рядка (стовпця) іншого рядка (стовпця) даної матриці, помноженого на відмінне від нуля число;
3. переставляння будь-яких двох рядків (стовпців) матриці.
Ранг матриці не зміниться після елементарних перетворень матриці.
Рангом матриціназивається максимальна кількість лінійно незалежних рядків або стовпців.
Ранг матриці можна знаходити такими методами:
метод обведення: даний метод ґрунтується на означенні рангу матриці як максимального порядку відмінного від нуля мінора;
метод Гаусса: за допомогою елементарних перетворень дану матрицю 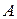 можна звести до вигляду
можна звести до вигляду
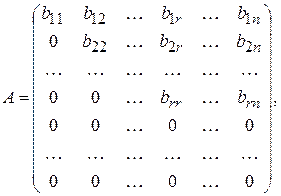
в якому всі елементи 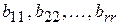 - не нульові, а елементи інших рядків, розміщені під ними, - нульові.
- не нульові, а елементи інших рядків, розміщені під ними, - нульові. 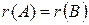 .
.
