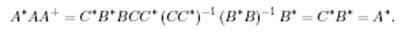Теорема 3. (5) векторлық теңдеудің шешім бар болу үшін
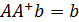(6)
болуы қажетті және жеткілікті. Бұл жағдайда жалпы шешім
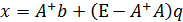(7)
түрінде берілуі мүмкін, мұндағы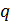 
- белгілі өлшемді кез келген вектор.
Дәлелдеу. (6) теңдіктің орындалуының қажеттілігі мен жеткіліктілігі 2-теоремадан шығады. Енді жалпы шешімі (7) теңдікпен берілетіндігін көрсетейік. (7) теңдік орындалсын делік және
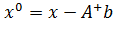(8)
векторын анықтайық.
Онда келесі тепе-теңдіктер тізбегі орындалады:
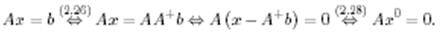
1-теореманың негізінде
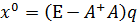
теңдігі орындалады, ал бұл (8) ескеретін болсақ
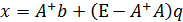
теңдігіне эквивалентті.
(7) теңдіктің бірінші қосылғышы (5) біртексіз теңдеудің дербес шешімі, ал екінші қосылғышы (1) біртекті теңдеудің жалпы шешімі болады.
Мысал 2. (біртексіз теңдеудің жалпы шешімі). Келесі біртексіз теңдеудің жалпы шешімін табайық:
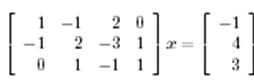(9)
Алдымен (9) теңдеудің үйлесімділігін тексерейік. Ол үшін 3-теоремадағы (6) шартты қолданайық. Алдыңғы дәрісте псевдокері матрицаны табу мысалында анықталған нәтижені пайдаланайық, сонда мынаны аламыз:
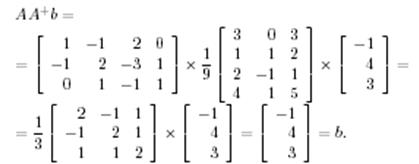
Демек (9) жүйе үйлесімді. Оның шешімін (7) түрінде құрайық. (7) –ң бірінші қосылғышын табайық:
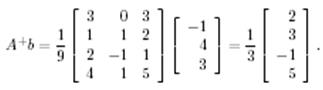
(7)-ң екінші қосылғышы бұл зерттеліп отырған біртексіз жүйеге сәйкес келетін біртекті жүйенің жалпы шешімі болады. онда біртексіз жүйенің жалпы шешімі келесі түрге ие болады:
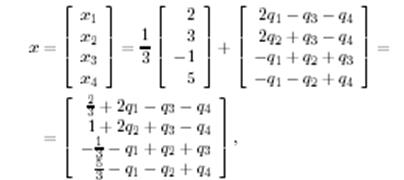
мұндағы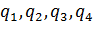 
- кез келген парметрлер.
(5)-ші жүйе кез келген 
үшін үйлесімді болады, егер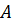 
матрицасы жол бойынша толық рангке ие болса. Егер жүйе үйлесімді болса, онда оның шешімі жалғыз болады, егер 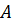матрицасы баған бойынша толық ранке ие болса. Егер 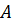матрицасы жол бойынша толық ранке және баған бойынша толық рангке ие болса, онда ол ерекше емес матрица болады және бұл жағдайда жалғыз ғана 
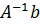шешімі бар.
Сызықтық теңдеулер жүйесінің қалыпты псевдошешімі
Векторлық түрде берілген сызықтық алгебралық теңдеулер жүйесін қарастырайық:
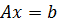(10)
Анықтама 1.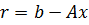 
векторы 
векторының байламсыздық векторы деп аталады.
Байламсыздықтың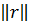 
ұзындығы векторы жүйенің шешіміне қаншалықты жақын болатындығын сипаттайды. Егер жүйенің шешімі болса, онда байламсыздық нөлге тең. Егер жүйе үйлесімсіз болса, онда байламсыздық әр уақытта нөлдік емес болады. Бұл жағдайда мынадай есепті қоюға болады: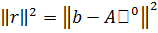 
шамасы ең кіші мән қабылдайтындай 
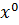векторын табу керек. Мұндай ұсынысты (подход) еің кіші квадраттар әдісі деп атайды.
Анықтама 2. Байламсыздық ұзындығы минималды болатын 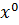векторы (10) жүйенің псевдошешімі деп аталады. Минималды ұзындықты псевдошешімді (10) жүйенің қалыпты псевдошешімі деп атайды.
Басқаша айтқанда, (10) жүйенің 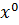қалыпты псевдошешімі, байламсыздықтың ұзындығын минимумға әкелетін барлық векторлардың арасында ең кіші ұзындыққа ие болатыны.
Теорема 4. (10) жүйенің псевдошешімі әрқашанда бар болады және ол жалғыз, сонымен қатар ол келесі формуламен анықталады:
.
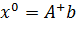Дәлелдеу. Кез келген бағанын қарастырайық және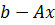 
айырымын келесі түрде келтірейік:
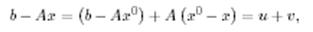
мұндағы
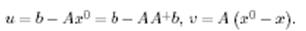
Онда
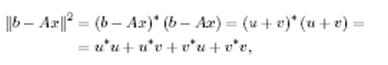(11)
Мұндағы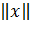 
- 
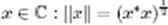векторының евклид ұзындығы. Алайда,
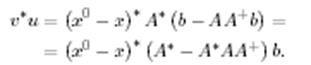(12)
9-дәрістегі (1) скелеттік жіктеуден және (12) псевдокері матрицаның негізінде мынаны аламыз:
