Решение систем линейных уравнений методом Гаусса

Линейная и квадратичная интерполяция

Интерполяция с помощью многочлена Лагранжа.

Численное дифференцирование методом конечных разностей.

Численное интегрирование методом прямоугольников и трапеции

Численное решение интегралов методом прямоугольников.

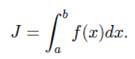
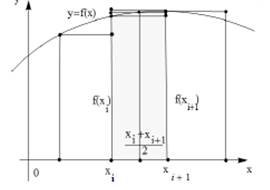
Делим на равные части. Шаг следования точек разбиения равен h=(b-a)/n. Заменим каждый интеграл ri площадью прямоугольников с основанием h и высотой f(xi), то есть hf(xi).

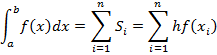
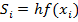
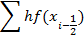
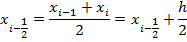
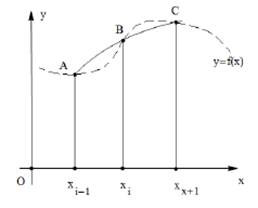
Численное решение интегралов методом трапеции.

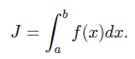
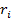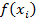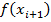Заменим каждый интеграл площадью трапеции с высотой h и основаниями длины и , то есть .

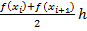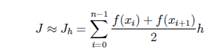
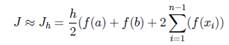
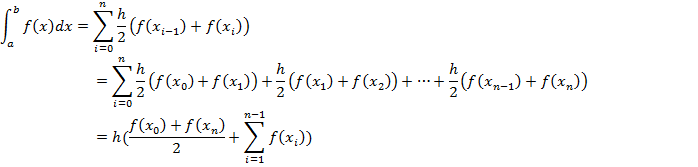
Численное интегрирование методом Симпсона

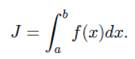
Делим на четное количество отрезков. Шаг следования h=(b-a)/2n.

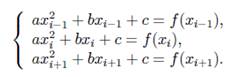
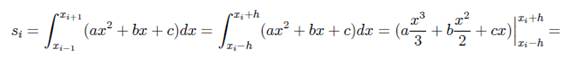
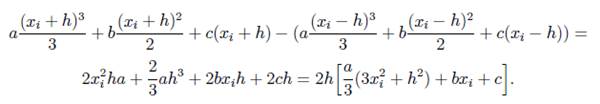
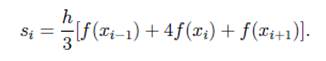
Численное интегрирование методом Монте-Карло.

Решение нелинейных уравнений методом деления отрезка пополам.

Метод деления отрезка пополам позволяет найти корень уравнения f(x)=0 на отрезке [a, b] при условии, что функция f(x) непрерывна и на концах отрезка принимает значения разных знаков: f(a)f(b)<0.

Суть метода деления отрезка пополам заключается в следующем. Находим середину отрезка [a, b], содержащего корень данного уравнения, и проверяем условие f(a)f(с)<0. Если условие есть True, то корень уравнения принадлежит отрезку [a, c], который и принимаем за новый отрезок, полагая b=c, а если False, то корень уравнения принадлежит отрезку [c, b], поэтому полагаем a=c. Проверяем условие остановки |b-a}<e. Если оно верно, то с и есть корень с данной погрешностью. Если оценка не верна, о повторяем процесс деления пополам для нового отрезка [a, b]. Вариант f(c)=0 сразу определяет корень.

Решение нелинейных уравнений методом Ньютона.

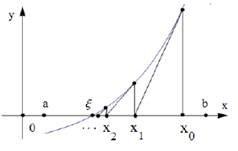
Метод Ньютона (или метод касательных) является итерационным методом решения уравнения с одной неизвестной f(x)=0 и характеризуется способом приведения этого уравнения к виду x=ф(x). Метод Ньютона заключается в следующем: пусть функция f(x), имеет единственный корень e на отрезке [a, b]. Возьмем точку х0 принадлежит [a, b].

Пусть касательная к графику функции y=f(x) в точке с абсциссой x0 пересекает ось х-ов в точке x1. Пусть касательная к графику функции y=f(x) в точке с абсциссой x1 пересекает ось х-ов в точке x2. Продолжая такие построения, получим последовательность точек {xn}n=0,1,2,… При соблюдении некоторых условии такая последовательность точек будет сходится к корню е.

Приведем формулу для вычисления элементов последовательности. Для этого напишем уравнение касательной к графику функции y=f(x) в точке ( 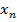, f( )): .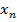

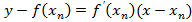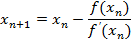
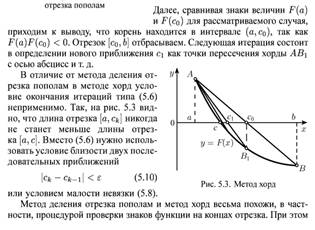
Решение нелинейных уравнений методом хорд.

Уравнение прямой через две точки

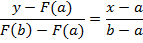
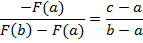
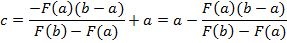
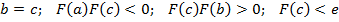
Решение систем линейных уравнений методом Гаусса

Рассмотрим систему линейных алгебраических уравнений (СЛАУ)

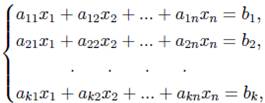
Прямой ход. Пусть коэффициент а11 не равен нулю. Поделим первое уравнение системы (ведущая строка) на элемент а11 (ведущий элемент):

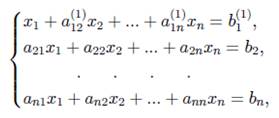
Здесь и далее индексами вида «(1)» обозначены соответствующие изменения коэффициентов. Исключим из такой системы переменную х1 из второго, третьего и так далее до n-го уравнения. Для этого из i-го уравнения системы вычитаем первое уравнение, умноженное на коэффициент 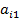. В результате приведем систему к следующему виду:

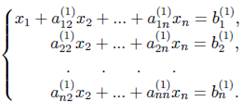
Далее, делим второе уравнение на коэффициент при х2 и исключаем переменную х2 из третьего и так далее до n-го уравнения. Повторяем этот процесс до последнего уравнения. Последнее уравнение поделим на коэффициент при неизвестной. Тем самым, равносильными преобразованиями, система уравнения будет приведена к треугольному виду.

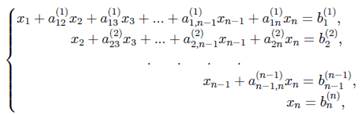
Обратный ход. Из последнего уравнения системы, содержащего одну переменную, находим 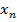. Найденное 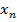подставляем в последнее уравнение и находим 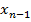, и так далее.