Критерий останова для метода многомерной оптимизации
Семестровые задания
по дисциплине “Методы оптимизации”
Разработка программной системы многомерной оптимизации.
Проведение численных исследований на наборе тестовых задач.
Составитель
доцент кафедры САПР и ПК к.ф.-м.н. Яновский Т.А. ______________
Волгоград 2011
Разработка программной системы
Составляющие элементы для системы численной оптимизации:
Метод(ы) многомерной безусловной оптимизации (реализуется в соответствии с номером задания)
1.Метод поиска по симплексу (метод прямого поиска)*
2.Методы случайного поиска – адаптивный и с возвратом при неудачном шаге**
3.Методы случайного поиска – адаптивный и метод наилучшей пробы**
4.Метод Розенброка**
5.Метод сопряженных направлений Пауэлла*
6.Метод сопряженных градиентов Флетчера-Ривса*
7.Метод Марквардта (модифицированный метод Ньютона)*
8.Метод Бройдена-Флетчера-Шэнно(квазиньютоновский метод)*
Изложен на стр. 128. При возникновении проблем со сходимостью метода Бройдена-Флетчера-Шэнно реализовать прием периодического возврата квазиньютоновской матрицы к единичной (как на первой итерации).
9.Проективный метод Ньютона-Рафсона с формулой пересчета
квазиньютоновской матрицы
* Описание метода приведено в первом томе работы Реклейтис, Г., Рейвендран, А., Рэгсдел, К. Оптимизация в технике: в 2 кн. – М.: Мир, 1986.
** Описание методов приведено в работе Пантелеев А.В., Летова Т.А. Методы оптимизации в примерах и задачах. – М.: Высшая школа, 2002.
Метод численной аппроксимации производных (реализуются обе схемы, аналитическое оценивание градиента не применяется)
1.Правая разностная схема
, h=0.01, 0.0001
2.Центральная разностная схема
, h=0.01, 0.0001
При вычислении вектора-градиента разностная схема (например, правая) применяется следующим образом:
Метод одномерной оптимизации для использования на итерациях метода многомерной оптимизации (реализуется один из списка в соответствии с номером задания)
1.метод золотого сечения с процедурой поиска начального отрезка локализации минимума;
2.метод деления пополам с процедурой поиска начального отрезка локализации минимума;
3.метод последовательной квадратичной аппроксимации Пауэлла;
4.метод Ньютона-Рафсона с процедурой поиска начального отрезка локализации минимума*;
5.метод средней точки с процедурой поиска начального отрезка локализации минимума*;
6.метод секущих с процедурой поиска начального отрезка локализации минимума*;
Также может быть выбран иной метод одномерного поиска (вариант необходимо предварительно согласовать с преподавателем).
* - описание метода см. в Приложении 1.
Критерий останова для метода многомерной оптимизации
(реализуются один критерий с двумя подвариантами из списка в соответствии с номером задания, а также критерий обязательной остановки метода по выполнению 100 итераций)
1. 
,
1. 
0.001
2. 0.0001
3. 0.00001
2. 
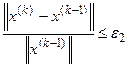
1. 
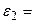0.01
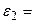2. 0.001
3. 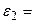0.0001
3. 
1. 
0.01
2. 0.001
3. 0.0001
4. 
1. 
0.01
2. 0.001
3. 0.0001
4. 0.00001
5. 
(для методов случайного поиска)
1. 0.1
2. 0.05
3. 0.01
Основные требования к программной системе: