И их основные следствия. Формула Байеса
10. УСЛОВНАЯ ВЕРОЯТНОСТЬ.
ВЕРОЯТНОСТЬ ПРОИЗВЕДЕНИЯ СОБЫТИЙ
Посмотрите на рис. 8.3. Множество  составляет часть множества
составляет часть множества 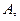 поэтому
поэтому 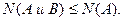 Величина
Величина
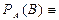
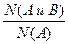
называется условной вероятностью. Более полное его название таково:
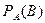 есть вероятность события
есть вероятность события  при условии, что
при условии, что  уже произошло.
уже произошло.
Запишем это равенство в виде 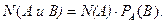 Обе части разделим на
Обе части разделим на 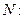
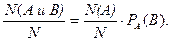
Получим
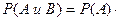 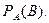 |
| Формула определения вероятности произведения событий. |
(10.1)
Ввиду того, что 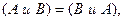 события
события  ,
,  можно менять ролями.
можно менять ролями.
Из формулы (10.1) можно получить вероятность произведения трёх событий:
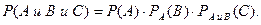
З а д а ч а 1. Буквы слова 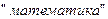 выписаны на отдельных карточках и перемешаны. Вы берёте 4 карточки одну за другой и укладываете по порядку. Найдите вероятность того, что появится слово
выписаны на отдельных карточках и перемешаны. Вы берёте 4 карточки одну за другой и укладываете по порядку. Найдите вероятность того, что появится слово 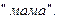
□ 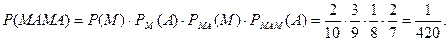 ■
■
11. НЕЗАВИСИМОСТЬ СОБЫТИЙ
Если 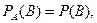 |
то говорим, что событие  не зависит от события не зависит от события 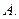 |
(11.1)
Формула (11.1) показывает, что событие  не влияет на вероятность появления события
не влияет на вероятность появления события 
Легко показать, что если  не зависит от
не зависит от 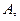 то и
то и  не зависит от
не зависит от 
¨ Дано:  не зависит от
не зависит от 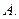 Тогда
Тогда
(11.1) 
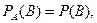 (а)
(а)
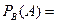
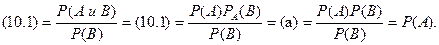 ■
■
Теперь докажем равносильность следующих утверждений
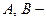 независимые события независимые события |
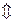 |
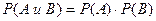 |
(11.2)
Аналогичная формула верна для любого числа независимых событий.
¨ 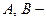 независимые события,
независимые события,
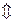 (11.1)
(11.1)
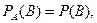
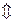
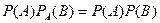
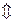 (10.1)
(10.1)
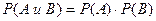 . ■
. ■
З а д а ч а 1. Два стрелка стреляют по цели. Вероятности их попаданий равны соответственно 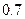 и
и 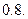 Найти вероятность того, что
Найти вероятность того, что
а) оба стрелка попадут в цель;
б) оба стрелка промахнутся;
в) первый стрелок попадёт, второй – промахнётся.
□ Вводим обозначения
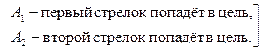 – независимые события.
– независимые события.
Тогда по условию 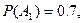
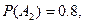
отсюда 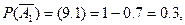
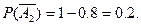
а) Вероятность того, что в цель попадёт первый стрелок и второй, равна
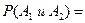 (11.2)
(11.2) 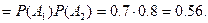
б) Вероятность того, что промахнётся первый стрелок и второй, равна
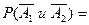
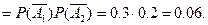
в) Вероятность того, что в цель попадёт первый стрелок, а второй промахнётся, равна
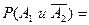
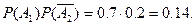 ■
■
12. ВЕРОЯТНОСТЬ СУММЫ СОБЫТИЙ
| Вероятность суммы двух событий определяется по формуле |
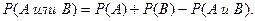 |
(12.1)
¨ Эта формула вытекает из (8.2) путём деления обеих частей на  ■
■
З а д а ч а 1. Из колоды, содержащей 36 карт, вынимаются две карты. Какова вероятность того, что среди них будет хотя бы одна дама?
□ Пусть 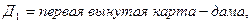
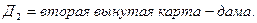
Вероятность появления хотя бы одной дамы будет равна
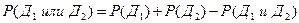
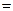
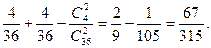 ■
■
Вероятность суммы событий можно определять и по другой формуле, которую можно распространить на любое число событий:
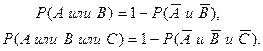 |
(12.2)
¨ 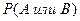
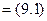
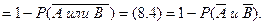 ■
■
З а д а ч а 2. Вероятности попаданий в цель из трёх орудий равны соответственно 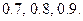 Найти вероятность попадания хотя бы из одного орудия при залпе из всех орудий.
Найти вероятность попадания хотя бы из одного орудия при залпе из всех орудий.
□ Пусть 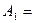 в цель попадёт первое орудие,
в цель попадёт первое орудие, 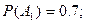
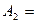 в цель попадёт второе орудие,
в цель попадёт второе орудие, 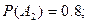
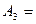 в цель попадёт третье орудие,
в цель попадёт третье орудие, 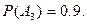
Тогда вероятность попадания хотя бы из одного орудия будет равна
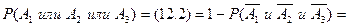
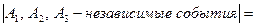
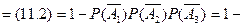
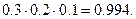 ■
■
Из формулы (12.1) получаем формулу, верную для любого числа событий:
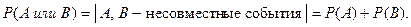 |
(12.3)
¨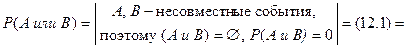
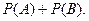 ■
■
13. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ
Если 1) 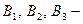 несовместные события (гипотезы), 2) когда произойдёт одно из них, может произойти событие несовместные события (гипотезы), 2) когда произойдёт одно из них, может произойти событие 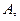 |
то 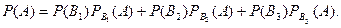 |
(13.1)
¨ Дано: 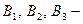 несовместные события, (а)
несовместные события, (а)
событие  может произойти вместе с
может произойти вместе с 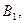 или с
или с 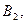 или с
или с 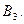 (б)
(б)
Тогда 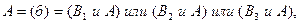 (в)
(в)
(а)  события
события 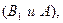
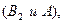
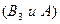 несовместны,
несовместны,
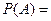
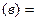
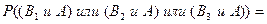
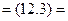
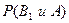 +
+ 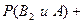
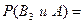
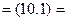
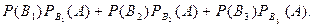 ■
■
З а д а ч а 1. В ящике лежат 40 деталей, изготовленных Уховым, 30 деталей, изготовленных Носовым и 20 деталей, изготовленных Криволаповым. Ухов допускает 6% брака, Носов – 5%, Криволапов – 3%. Найти вероятность того, что наудачу взятая деталь не будет бракованной.
□ Пусть  наудачу взятая деталь не будет бракованной.
наудачу взятая деталь не будет бракованной.
Введём 3 гипотезы:
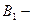 деталь изготовлена Уховым, тогда
деталь изготовлена Уховым, тогда 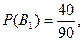
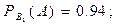
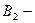 деталь изготовлена Носовым, тогда
деталь изготовлена Носовым, тогда 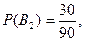
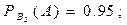
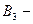 деталь изготовлена Криволаповым, тогда
деталь изготовлена Криволаповым, тогда 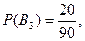
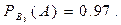
По формуле (13.1) получаем
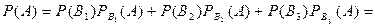
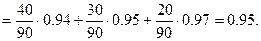 ■
■
14. ФОРМУЛА БАЙЕСА
Если 1) 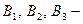 несовместные события (гипотезы), 2) когда произойдёт одно из них, может произойти событие несовместные события (гипотезы), 2) когда произойдёт одно из них, может произойти событие 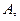 |
то 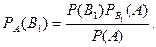 |
(14.1)
В этой формуле знаменатель 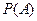 вычисляется по формуле (13.1).
вычисляется по формуле (13.1).
¨ Так как 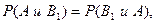
то по формуле (10.1) будем иметь 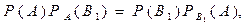
отсюда 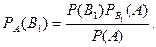 ■
■
З а д а ч а 1. Пусть в ситуации, описанной в предыдущей задаче, произошло событие: наугад взятая деталь оказалась небракованной. Какова вероятность того, что она изготовлена Уховым?
□ Введём те же обозначения, что и в предыдущей задаче. Так как теперь произошло событие  наудачу взятая деталь оказалась небракованной, то вероятность события
наудачу взятая деталь оказалась небракованной, то вероятность события 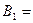 деталь изготовлена Уховым, найдётся по формуле Байеса:
деталь изготовлена Уховым, найдётся по формуле Байеса:
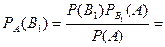
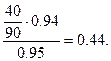 ■
■
15. ФОРМУЛА БЕРНУЛЛИ
Если а) испытание повторяется  раз, б) результаты испытаний не зависят друг от друга, в) вероятность раз, б) результаты испытаний не зависят друг от друга, в) вероятность 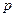 появления события появления события  одинакова во всех испытаниях, одинакова во всех испытаниях, |
то вероятность того, что  произойдёт произойдёт  раз, равна раз, равна 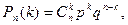 |
где 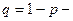 вероятность непоявления вероятность непоявления 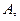 одинаковая во всех испытаниях. одинаковая во всех испытаниях. |
¨ Дано: выполнены условия а, б, в. Заметим, что опыт состоит в повторении испытания  раз. Приведём один из возможных благоприятных шансов:
раз. Приведём один из возможных благоприятных шансов:
| Номер испытания | 1 2 3 4 … n - 1 n | ||||||||
| Появление события A |
| Количество единицравно k, количество нулей равно n - k. | |||||||
| Вероятность | q p p q … q p |
Вероятность этого шанса равна 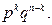 Таких шансов равно числу способов выбрать
Таких шансов равно числу способов выбрать  клеток (в которые мы вписываем 1) из
клеток (в которые мы вписываем 1) из  имеющихся, т. е. равно
имеющихся, т. е. равно 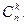 Эти шансы несовместны, поэтому согласно (12.3)
Эти шансы несовместны, поэтому согласно (12.3) 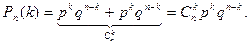 ■
■
Рассмотрим частный случай, когда 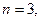
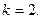 Введём события
Введём события 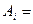 событие
событие  произойдёт в
произойдёт в 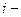 м испытании. Тогда
м испытании. Тогда
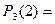
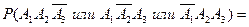 (12.3)
(12.3) 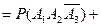
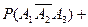
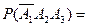
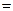 (б), (в)
(б), (в) 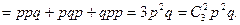
З а д а ч а 1. Вероятность попадания в цель при одном выстреле равна 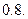 Найти вероятность
Найти вероятность 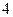 попаданий при
попаданий при 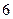 выстрелах.
выстрелах.
□ Дано 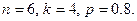
Тогда 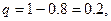
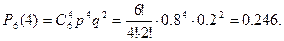 ■
■
16. ПРИБЛИЖЁННЫЕ ФОРМУЛЫ,
ВЫТЕКАЮЩИЕ ИЗ ФОРМУЛЫ БЕРНУЛЛИ
Когда число опытов  велико, вычисления по формуле Бернулли становятся громоздкими из-за необходимости вычислять факториалы больших чисел. В таком случае применяют приближённые формулы, точность которых повышается при увеличении
велико, вычисления по формуле Бернулли становятся громоздкими из-за необходимости вычислять факториалы больших чисел. В таком случае применяют приближённые формулы, точность которых повышается при увеличении  Приведем формулы без их вывода.
Приведем формулы без их вывода.
1.Формула Пуассона.
Если 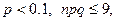 |
то 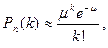 |
где 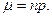 |
(16.1)
З а д а ч а 1. Вероятность изготовления нестандартной детали равна 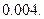 Найти вероятность того, что среди 1000 деталей окажутся 5 нестандартных.
Найти вероятность того, что среди 1000 деталей окажутся 5 нестандартных.
□ Имеем 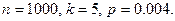 Тогда
Тогда 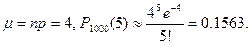 ■
■
2. Локальная формула Лапласа.
Если 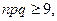 |
то 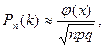 |
где 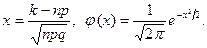 |
(16.2)
 Значения функции
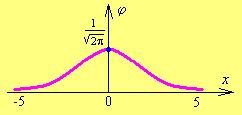
Значения функции 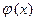 можно брать из таблиц, которые обычно имеются в учебниках по теории вероятностей. Эта функция чётная,
можно брать из таблиц, которые обычно имеются в учебниках по теории вероятностей. Эта функция чётная, 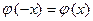 (рис. 16.1). При удалении от начала координат
(рис. 16.1). При удалении от начала координат 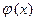 стремится к нулю так быстро, что при
стремится к нулю так быстро, что при 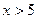 считают, что
считают, что 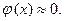
Так как 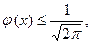 то из 16.2) следует, что
то из 16.2) следует, что
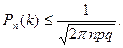
Рис. 16.1
З а д а ч а 2. Найти вероятность того, что при 600 выстрелах
мишень будет поражена 250 раз, если вероятность попадания при одном выстреле равна 0.4.
□ Имеем 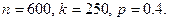 Тогда
Тогда 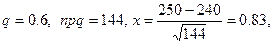
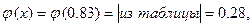
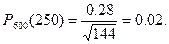 ■
■
