Белгілеулер мен ҚысҚартулар

ШТ – Шредингер теңдеуі

ТФ – толқындық функция

ОӨ – осцилляторда өрнектелу

ДАТЕТ –дискретті айнымалының түзу емес туындысы

АТ – ауытқу теориясы

КІРІСПЕ

Қазіргі таңда ультрасуық атомдар мен молекулалар физикасы (кванттық газдар физикасы) 1995 жылы бозе-эйнштейн конденсациясы экспериментті түрде ашылғалы бері (2001ж. Нобел сыйы) шұғыл дамуда. Бұл бағыт бойынша жариялымдар (әсіресе эксперименттік жұмыстар бойынша) [1-3] өсуде. Бұл саланың соңғы жылдардағы таңқаларлық эксперименттік жетістіктері [4,5] кішіөлшемді кванттық жүйелер мен қатты коррелирленген көпбөлшекті жүйелерін зерттеу үшін айрықша мүмкіндіктер туғызуда.

Ультрасуық атомдар және молекулалармен тәжірибе жасау кезінде бөлшектер қозғалысы бір немесе екі айнымалы бойымен «оқшауландырылған» болып табылады, оптикалық потенциалды қолдана отырып оның динамикасы жазықтықта немесе сызықпен шектелген болады. Бұл жағдайда, төмен өлшемді жүйелердің физикалық қасиеттері оптикалық тұзақтың әсерінен айтарлықтай өзгеруі мүмкін. Сонымен қатар, тұзақ параметрлерін өзгерте отырып, атомаралық әсерлесулерді тиімді басқаруға болады. Бұл күшті корреляцияланған кванттық жүйелерді [4], төмен өлшемді жүйелердегі азбөлшекті және көпденелі эффекттерді [2, 3], молекулаладың құрылуы кезіндегі жаңа механизмдерді [6], кванттық компьютер үшін мүмкін элементтерді [4] және т.б. зерттеу үшін жаңа мүмкіндіктер ашады.

Ультрасуық атомдар бойынша зерттеулер асқын өткізгіштік, асқын аққыштық [2], кванттық компьютер элементтеріне қолданылатын молекулалардың пайда болуымен жүретін химиялық реакциялар [7,10], сонымен қатар «Үлкен Жарылыстың» алғашқы кезінде пайда болған кварк-глюондық плазма [10,11] сияқты физикалық құбылыстарды басқару және модельдеу мүмкіндігіне байланысты қызығушылық тудырады.

Бұл тақырып бойынша зерттеулер әлемнің барлық үлкен ғылыми орталықтарында заманауи теориялық физиктер дамытушы бағыттың бірі. Бұл зерттеулер тек академиялық қызығушылық қана емес, сонымен қатар практикалық маңыздылығы зор. Жоспарланған нәтижелер ультрасуық атомдар мен молекулаларды зерттеуші эксперименттерді жоспарлау мен өңдеуге өте қажет және маңызды, себебі қазіргі таңда теориялық моделдер бұл бағыттағы эксперимент қажеттілігінен артта қалуда.

Бертінге дейін қолданылған азбөлшекті кванттық процестерді бейнелеуге арналған теориялық модельдер [3,6] бұл саладағы заманауи тәжірибелердің қажеттіліктерін қанағаттандыра алмайды. Ультрасуық кванттық жүйелердің жан-жақты тәжірибелік шолулары осы молекулалардың қасиеттерін теориялық зерттеуді қажет етеді. Олардың интерпретациясы және жаңа тәжірибелерді жоспарлау үшін бар теориялық модельдерді жақсарту және жаңа теориялық модельдерді дамыту үшін жұмыстар жүргізілуі керек.

Көптеген теориялық зерттеулер негізінен бірөлшемді және екіөлшемді гармоникалық тұзақтардағы екіатомды жүйелердің шашырау параметрлеріне арналған қарапайым бірөлшемді жартылай аналитикалық М.Ольшано (1998 ж.) және Г. Шляпников (2001 ж.) моделдеріне негізділген [6-10]. Атомаралық әсерлесу ретінде бұл жұмыстарда жеңілдетілген дельта түрдегі потенциал қолданылады [8,9]. [12-15] жұмыстарында геометриясы шектеулі гармоникалық тұзақтың нақты әсерлесуі бар қосатомды жүйелерді сандық зерттеу әдістемелері дамытылған. Жаңа нәтижелер алынған (тұзақтағы кванттық шашыраудың өшу әсері байқалған, тұзақта қосатомды молекулалардың резонансты түзілуінің жаңа механизмі ұсынылған, т.б. ) және де тұзақ ангармонизмінің спектрге, азөлшемді кванттық жүйелердің шашырау параметрлеріне әсері сияқты киынырақ әсерлемелерді зерттеу үшін ыңғайлы “плацдарм” жасалған. Екінші жағынан, ангармонизм әсерін зерттеудің өзекті әрі тиімді әдісі болып осцилляторда өрнектелу[16] табылады. Бұл әдіс соңғы кездері отандық ғалымдармен [17] сәтті зерттелуде. Осы әдістеме ангармоникалық осциллятордың төмен орналасқан күйлерін есептеуге сәтті қолданбақшы. Екі әдістеме де бұл жұмыс барысында нақтырақ әсерлесуі бар түрлі конфигурациялы оптикалық тұзақтағы байланысқан күйлер мен екіатомдық кванттық және үшөлшемді моделдік жүйелер үшін шашырау параметрлерін есептеу ретінде өңделмекші.

Диссертация барысында зерттеудің негізгі әдістері ретінде осцилляторда өрнектелу әдістері [16-19] мен кішіөлшемді кванттық жүйелерді сандық зерттеу әдістері [12-15] қолданылады. Бұл екі әдістеме соңғы жылдары кванттық физиканың күрделі есептеріне жоғары маңыздылықтарын көрсетті. Әсіресе, гармоникалық тұзақта масса орталығында түрлі атомдардың соқтығысуының салыстырмалы қозғалысының әсерін ескеруге төртөлшемді Шредингер теңдеуін сандық интегралдауға арналған арнайы әдіс дамытылған. Бұл әдістерді ангармоникалық атомдық тұзақта айнымалылары ажыратылмайтын масса орталықтары бар және салыстырмалы қозғалыстағы екіатомды есептерге колданамыз. Осцилляторда өрнектелу үшденелі кванттық жүйелердің спектрін зерттеуге жақсы игерілген [19].

1 БІР ӨЛШЕМДІ ГАРМОНИКАЛЫҚ ТҰЗАҚТЫҢ ШЕКТЕЛГЕН ГЕОМЕТРИЯСЫНДАҒЫ ЕКІ ДЕНЕ КВАНТТЫҚ ЕСЕБІН ШЕШУ ӘДІСТЕРІ

Қарастырылып отырған есептердің сандық талдануы үшін, бұрыштық айнымалылар бойынша дискретті торда құрастырылған арнайы екіөлшемді базисті қолдана отырып, Шредингердің үшөлшемді теңдеуін сандық интегралдау үшін [13-15] жұмыстарда берілген әдісті қолданамыз. Мұнда біз стационарлы және стационар емес жағдайларға әдістің негізгі бөлігін баяндаймыз.

Бірінші координаталары r_1, r₂ және массалары 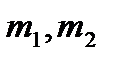болатын екі әртүрлі атомның динамикасын 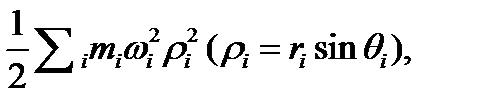гармоникалық потенциалда қарастырамыз, ол Шредингердің стационар емес теңдеуімен бейнеленеді

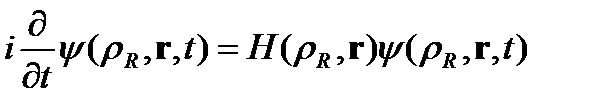
Гамильтонианы

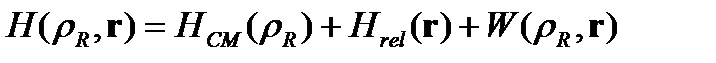(1.1)

мұнда

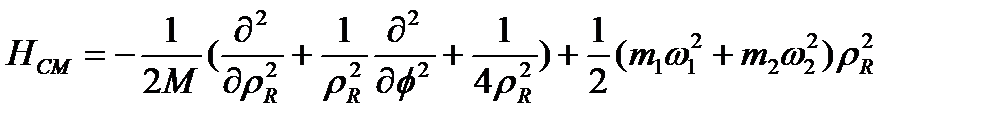(1.2)

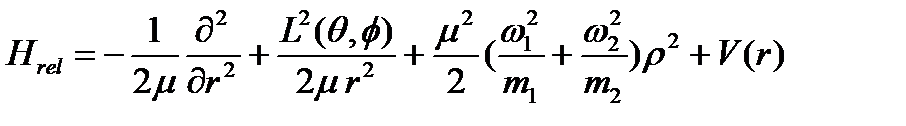(1.3)

гамильтониандары массалар орталығының қозғалысын және атомдардың салыстырмалы қозғалысын сипаттайды. 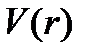-потенциалы атомаралық әсерлесуді бейнелейді, 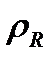және 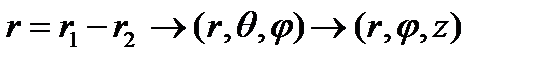массалар орталығының және салыстырмалы қозғалыстың полярлық координаталары және , .

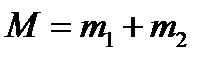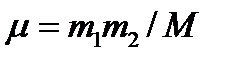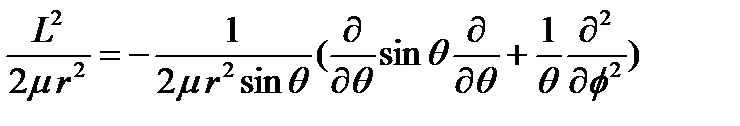
қосылғышы атомдардың салыстырмалы қозғалысының кинетикалық энергия операторының бұрыштық бөлігін көрсетеді.

Қосылғышта

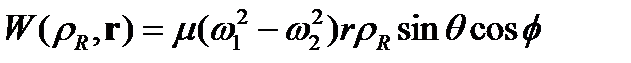(1.4)

бар болуы (1.1) гамильтонианында гармоникалық тұзақтың көлденең ұстап тұратын потенциалындағы массалар орталығы мен атомдардың салыстырмалы қозғалыс айнымалыларының бөлінбеуіне әкеледі, өйткені айырмалы атомдар жағдайында әрбір атом өзінің меншікті жиілігін 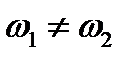“сезеді”. (1.4) теңдігінен шығатыны, 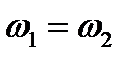бірдей атомдар жағдайында, 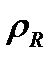және 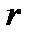айнымалылары бөлінеді де мәселе айтарлықтай жеңілдейді.

Бұл жұмыс оптикалық тұзақтың ангармонизм эффекттерін ескеруге бағытталған, бұл жағдайда массалар орталығының және салыстырмалы қозғалыстың айнымалылары 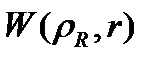операторында бөлінбейді, және тіпті бірдей атомдар жағдайында, дегенмен (1.4) оператор құрылымы гармоникалық тұзақ жағдайынан өзгеше. Ангармоникалық тұзақтың басқа маңызды ерекшелігі – атомдардың тұзақ қабырғалары арқылы туннельдену мүмкіндігі [28].

Шредингер теңдеуін интегралдау 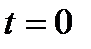-ден 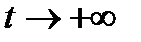асимптотикалық аймаққа дейін толқындық пакет үшін мынадай бастапқы шартпен орындалады:

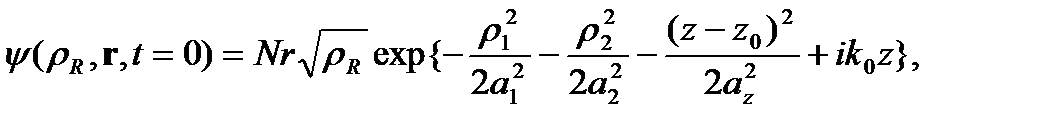(1.5)

Ол 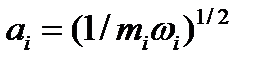бар көлденең тұзақтың негізгі күйіндегі екі әсерлеспейтін атомдарды көрсетеді, мұндағы 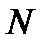нормалау шартымен 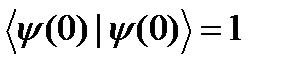анықталады. Мұндай бастапқы шарт салыстырмалы соқтығысу жылдамдығы 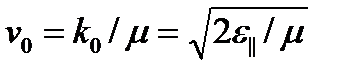болған кезде атомның атомда шашырауын зерттеуге мүмкіндік береді (анықталатын бойлық соқтығысу энергиясы 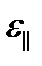). 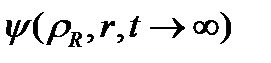шашыраған толқындық пакетті зерттей отырып, асимптотикалық аймақтағы шашырау параметрлерін анықтауға, сонымен қатар екіатомдық молекулалардың пайда болу ықтималдығын анықтауға болады. Атомдардың тұзақпен әсерлесуінің ангармоникалық потенциалы жағдайында тұзақтың бүйір қабырғасы арқылы (соңғы енінің потенциалы), тұзақтың квази-еркін атомдары арқылы, сонымен қатар, екіатомдық молекулалардың байланысқан күйлері арқылы (яғни тұзақтағы атомдық және молекулалық деңгейлер енін бағалау) туннельдеу ықтималдығын есептеу қызығушылық тудырады. Бұл жағдайдағы бастапқы жуықтау болып 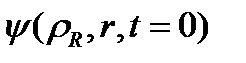тұзақтағы атомдық немесе молекулалық күйлер алынады.