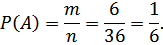Классическое определение вероятности

МИНИCTEPCTBO ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение

Высшего профессионального образования

«СЕВЕРО-КАВКАЗСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Методические указания к практическим занятиям и самостоятельной работе для студентов специальностей 090105. 65 « Комплексное обеспечение информационной безопасности», 090303.65 «Информационная безопасность автоматизированных систем», 090301.65 «Компьютерная безопасность», направлений подготовки 230700.62 «Прикладная информатика», 090900.62 «Информационная безопасность», 231300.62 «Прикладная математика»

Ставрополь 2013

Методические указания предназначены для оказания помощи студентам при выполнении самостоятельной работы. Указания содержат рекомендации по организации работы, список литературы составлены в соответствии с программой дисциплины «Теория вероятности и математическая статистика» для студентов специальностей 090105. 65 «Комплексное обеспечение информационной безопасности»

Составили: к. ф - м. н., профессор Адамчук А. С.,

к. ф - м. н., доцент Амироков С.Р.

Содержание

1. Формулировка заданий и его объем……………..............................................4

1.1. Теория вероятности…………………..............................................................4

1. 1. 1. Классическое определение вероятности…………..….............................4

1. 1.2. Теорема сложения и умножения вероятности…………...........................6

1. 1. 3. Формула полной вероятности....................................................................9

1. 1.4. Формула Бернулли……………….............................................................10

1. 1.5. Варианты контрольных работ...................................................................12

1.2. Математическая статистика..........................................................................28

1.2. 1. Задания на самостоятельную работу........................................................28

1. 2. 2. Генеральная совокупность и выборка.....................................................30

1, 2. 3. Интервальный вариационный ряд...........................................................30

1.2.4. Вычисление числовых характеристик...................................................... 33

1.2.5. Точечная и интервальная оценки числовых

характеристик генеральной совокупности..........................................................37

1.2. 6. Понятие о критериях согласия…………………………………………..38

1. 2. 7. Решение типового примера......................................................................39

1. 2. 8. Варианты заданий для математической статистики..............................45

1.3. Регрессионный и корреляционный анализ..................................................55

1.3. 1. Парная регрессия и корреляция................................................................55

1. 3. 2. Решение типового примера и задания.....................................................58

2. Рекомендации по организации выполнения контрольной работы Примерный календарный план ее выполнения..................................................74

3. Список рекомендуемой литературы................................................................75

4. Приложения (таблицы)...……………………………………………………..76

Формулировка заданий и его объем

Самостоятельная работа состоит из трех разделов:

а) Решение задач по основам теории вероятности. Задания содержат по шесть задач. Номер соответствующей задачи определяется номером варианта. Например, вариант 5 содержит задачи. 1. 5; 2. 5; 3. 5; 4. 5; 5. 5; 6. 5.

б) Знакомство с основными задачами статистики. Оценка характеристик генеральной совокупности по выборке. Задание общее. Данные выборки приведены в приложении, номер выборки соответствует варианту.

в) Выполнение работы по регрессионному и корреляционному анализу.

Задание общее, данные соответствуют варианту.

Теория вероятности

Классическое определение вероятности

В теории вероятности одним из основных понятий является событие.

Наблюдаемые нами события можно разделить на достоверные, невозможные и случайные.

Достовернымназывается событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий.

Невозможнымназывается событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий.

Случайныминазывают событие, которое может произойти, либо не произойти, если будет осуществлена определенная совокупность условий.

Вместо слов «осуществлена совокупность условий» зачастую говорят «произведено испытание».

События называют несовместными,если появление одного из них исключает появление других событий в одном и том же испытании.

Система событий образует полную группудля данного испытания, если любым исходом его является одно или только одно событие этой группы.

Возможные, исключающие друг друга, результаты одного испытания называются элементарными исходными испытаниями.

Исход испытания называется благоприятствующимнекоторому событию, если в результате этого исхода появляется указанное событие.

События называются равновозможными,если нет оснований считать одно из них более или менее возможным, чем остальные.

Определение.Вероятностью 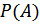события А называют отношение числа благоприятствующих этому событию исходов m к общему числу п всех равновозможных элементарных исходов события, образующих полную труппу, т. е.

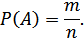
Свойства вероятности:

1. Вероятность достоверного события равна единице.

2. Вероятность невозможного события равна нулю.

3. Вероятность случайного события есть число, заключенное между нулем и единицей.

Таким образом, вероятность любого события А удовлетворяет неравенству;

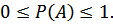
Пример 1

Игральная кость бросается два раза. Какова вероятность того, что сумма очков равна семи?

Решение

Число возможных исходов испытания n=36. Событию А, заключающемуся в том, что сумма очков равна 7, благоприятствуют исходы испытания (1,6), (6, 1), (2, 5), (5, 2), (3, 4), (4, 3). Следовательно, m=6. Значит