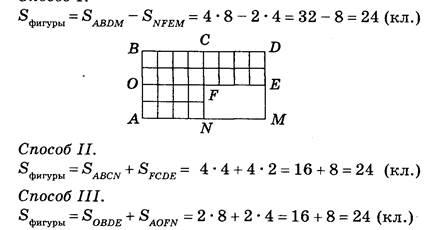
Проверка домашнего задания. Задание 3. Количество клеток можно подсчитать по-разному, дополнив фигуру до прямоугольника или разделив ее на части — прямоугольники.

3. Устный счёт.

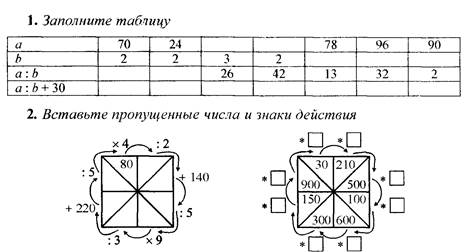
Задания 7, 5, 3.

Задание 3. Количество клеток можно подсчитать по-разному, дополнив фигуру до прямоугольника или разделив ее на части — прямоугольники.

Задание 7. Ответ формулируем с помощью число­вого луча:

а) ищем на луче числа 17 и 20, называем числа между ними (18, 19), проверяем правильность неравенств; б) b= 11, 12, 13, 14.

Сообщение темы и целей урока.

Изучение нового материала.

Задания 1, 2,4* (6 — выходит за рамки про­граммы ).

Сначала обсуждаем условие задачи и рисунок, за­тем составляем таблицу и записываем решение.

	Скорость	Время	Расстояние
I II	4 км/ч   1 3 км/ч	?	14 км

Чему равна скорость сближения пешеходов? 4 + 3 = 7 (км/ч)

Значит, за 1 ч вместе они проходят 7 км. За сколько, часов они пройдут вместе расстояние в 14 км?

14 : 7 = 2 (ч)

Расстояние в 14 км пешеходы пройдут вместе за 2 ч, а так как они идут навстречу друг другу, то через 2 ч они встретятся.

Задание 4*.

□ :8 =(ост. 7)

□ : 9 = (ост. 6)

Наименьшее делимое будет тогда, когда получим наименьшее частное. Проверим частное, равное 1.

□ : 8 = 1 (ост. 7), тогда делимое 15 (8 • 1 + 7 = 15). Проверим второе равенство при этом делимом. 15:9 = 1 (ост. 6)

9∙1 + 6 = 15. Числа совпадают.

Ответ: число 15.

Закрепление изученного материала.

Задание 6.

Подведение итогов урока.

Домашнее задание.

Задания 8, 9.

100. Тема урока. Задачи на встречное движение. Закрепление вычислительных приемов.(с. 68-69)

Цели урока: 1) показать два способа решения задач рассматриваемого вида;

2) отрабатывать вычислительные навыки.

3) воспитывать интерес к предмету.

Ход урока

1. Организационный момент.

2. Проверка домашнего задания.

3. Устный счёт.

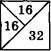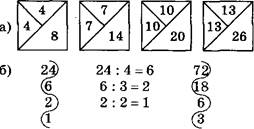72 : 4 = 18 18 : 3 = 6 6:2 = 3

(У) Задание 7*.

Сообщение темы и целей урока.

Изучение нового материала.

Задания 3, 4, 5, 6 (1 б, 2 — выходят за рамки программы ).

Обсуждаем условие задачи, составляем таблицу и записываем два способа решения.

Способ I.

1) 65∙4 = 260 (км)

2) 560 - 260 = 300 (км)

3) 300 : 4 = 75 (км/ч)

Способ II.

4) 560:4 = 140 (км/ч) — скорость сближения.

5) 140-65 = 75 (км/ч)

Задание 4.

Задание 5.

Р = 2 • 4 = 8 (см)
Если увеличить сторону в 2 раза, периметр будет равен:

р = (2 • 2) • 4 = 16 (см).

Значит, он тоже увеличился в 2 раза.

Закрепление изученного материала.

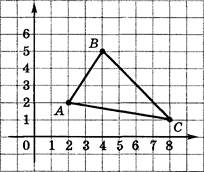
Задание 6. Учитель обращает внимание учеников на то, как построить оси координат и как по двум чис­лам (координатам) найти точки.

Подведение итогов урока.

Домашнее задание.

Задания 8, 9.

101. Тема урока. Умножение числа на произведение и произведения на число.

(с. 70 -71)

Цели урока: 1) помочь ученикам открыть сочета­тельный закон умножения;

2) решать задачи на движение.

3) воспитывать активность на уроке.

Ход урока

1. Организационный момент.

2. Проверка домашнего задания.

3. Устный счёт.

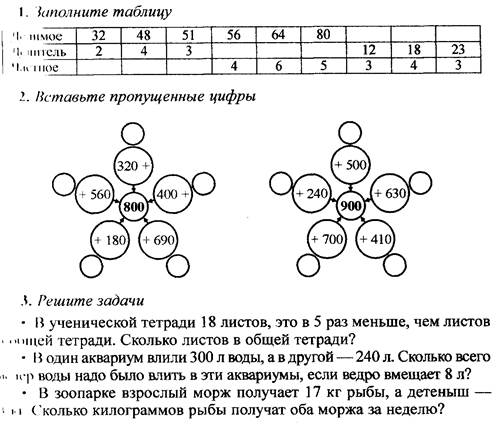
Задания 7, 3, 6*.

Задание 3. Ответ: 253, 263.

Задание 6*. Прочитайте, что обозначает стрелка, которая идет от дуба к сосне. (Дуб растет медленнее сосны.) Что обозначает стрелка, которая идет от сосны к березе? (Сосна растет медленнее березы.) Сделайте вывод про скорости роста дуба и бе

резы. (Дуб растет медленнее березы.) Что обозначает стрелка, которая идет от березы к бамбуку? (Береза растет медленнее бамбука.) Сделайте вывод про скорости роста дуба и бамбука. (Дуб растет медленнее бамбука.)

Сравните скорости роста кактуса, дуба и сосны. (Кактус растет медленнее дуба. Дуб растет медленнее сосны. Значит, кактус растет медленнее сосны.)

Сравните скорости роста сосны, березы и бамбу­ка. (Сосна растет медленнее березы. Береза растет медленнее бамбука. Значит, сосна растет медленнее бамбука.)

Задание 7. (156 • 3) • 2 = (156 • 2) • 3 — верное ра­венство, потому что от перестановки множителей про­изведение не меняется. 156 повторяется слагаемым 6 раз в левой и правой частях равенства.

6 • (3 • 58) < 58 • (3 • 6) — неравенство неверное.

6 • (3 • 58) = 58-(3 • 6) — используется перемести-тельное свойство умножения.

(115 • 2) • 3 = 115 • (2 + 3) — неверное равенство. В левой части 115 повторяется слагаемым 6 раз, а в правой 115 повторяется слагаемым 5 раз. Потому (115 • 2)-3> 115-(2 + 3).