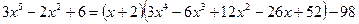Обчислення значення полінома та його похідних у точці.

ОБОВ’ЯЗКОВА КОНТРОЛЬНА РОБОТА №2

ПОЛІНОМИ

Кубічні рівняння.

Загальне кубі́чне рівня́ння — рівняння виду

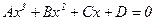, (1)

де 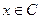- змінна, 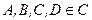- сталі, .

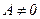Розділимо (1) на 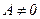. Одержимо зведене кубічне рівняння

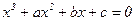(2)

Для того, щоб отримати загальний розв'язок кубічного рівняння, потрібно його звести до неповного кубічного рівняннязастосувавши підстановку

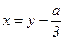. (3)

Неповне кубічне рівняння має вигляд.

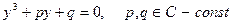(4)

Це можна зробити провівши заміну змінної

Одним з найвідоміших методів розв’язання канонічного кубічного рівняння є Метод Гудде.

Розглянемо його детальніше.

Розглянемо неповне кубічне рівняння (4)

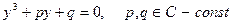
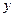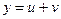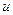Представимо невідому у вигляді , де і 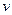- допоміжні невідомі. Це завжди можливо. Підставимо 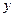у рівняння, отримаємо

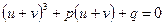
Після перетворення отримаємо

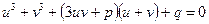
Введемо додаткову умову для невідомих, а саме:

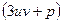=0

З цієї умови маємо

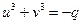
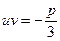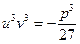або (5)

Маємо суму і добуток двох невідомих - 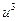та 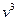. Якщо прийняти 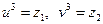, то за теоремою Вієта такі невідомі є коренями квадратного рівняння

.

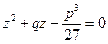Розв’язок цього рівняння буде таким

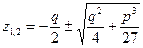або

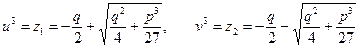
З останнього маємо

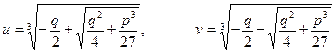
Оскільки кубічний радикал для комплексних чисел має три значення, і, відповідно, невідома 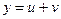приймає дев’ять різних значень,то нам необхідно мати спосіб відібрати з цієї множини 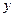ті, які дійсно є коренями рівняння (4). Таким способом відбору є (5):

З цієї формули витікає співвідношення між 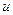і :

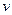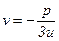. (6)

Отже ми на практиці можемо обчислити будь який з трьох радикалів для 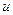, а далі 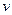знайти з формули (6).

Перший корінь неповного кубічного рівняння (4) згідно припущення 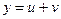буде

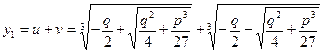, (7)

Або

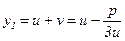
Два інших кореня рівняння (4) дають формули

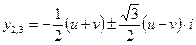* (8)

Формула (7) називається формулою Кардано для розв’язання кубічних рівнянь.

Аналіз розв’язків кубічного рівняння (4) проводять з використанням дискримінантурівняння .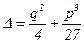

Мають місце такі випадки:

1. 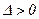- рівняння (4) має один дійсний і два уявні корені.

2. 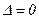- рівняння (4) має три дійсних кореня, причому два з них співпадають. Інколи співпадають усі 3 кореня.

3. 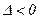- рівняння (4) має три простих дійсних кореня.

Після знаходження коренів канонічного кубічного рівняння (4) необхідно знайти корені зведеного рівняння (2). Для цього необхідно у заміну 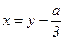підставити значення коренів .

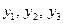Приклади

Приклад 1 Розв’язати кубічне рівняння:

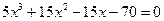
Розв’язання.

1. В цьому рівнянні 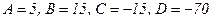. Зводимо кубічне рівняння, розділивши ліву і праву частину на :

,

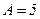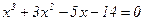Отримали, що .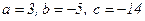

Виконаємо підстановку (3), отримаємо неповне кубічне рівняння:

.

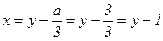Підставимо у рівняння

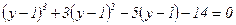
Розкриємо дужки

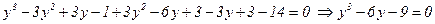
Неповне кубічне рівняння -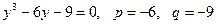

2. Виконаємо аналіз. Обчислимо дискримінант рівняння.

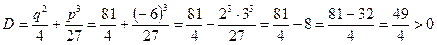, отже маємо випадок 1 – рівняння має один дійсний корінь і два уявні.

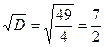
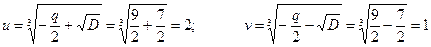
Перевіряємо зв’язок 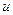і 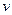за (5): 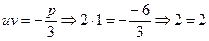. Зв’язок виконується.

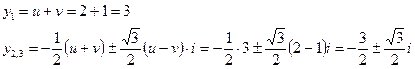
Розв’язок вихідного рівняння знайдемо виконавши заміну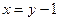

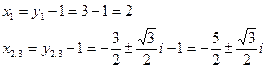
Відповідь

Кубічне рівняння 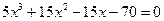має розв’язки

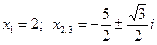
Перевірка.

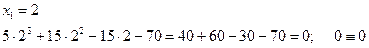
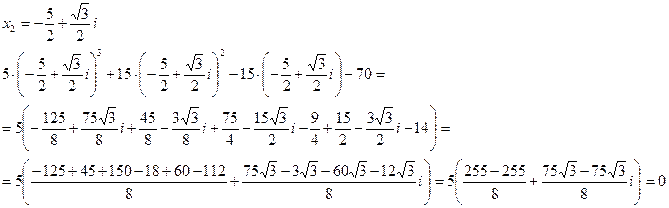
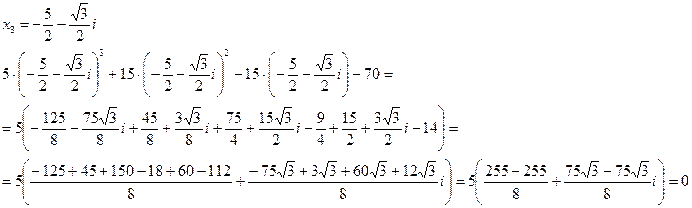Усі три кореня задовольняють рівняння.

Приклад 2 Розв’язати кубічне рівняння:

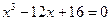
Розв’язання.

Дане рівняння має одразу неповний вигляд, 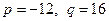. Проведемо аналіз рівняння. Обчислимо дискримінант:

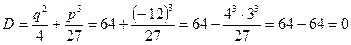- рівняння має 3 дійсних кореня, причому 2 з них однакові.

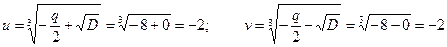
Перевіряємо зв’язок 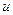і 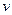за (5): 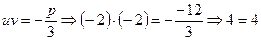. Зв’язок виконується.

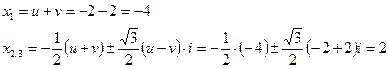
Відповідь

Кубічне рівняння 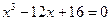має розв’язки

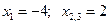
Перевірка.

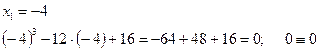
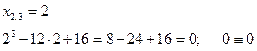
Усі три кореня задовольняють рівняння.

ІНДИВІДУАЛЬНЕ ЗАВДАННЯ 1.

Знайти корені кубічного рівняння 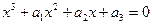за формулами Кардано

Коефіцієнти 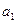, , 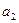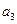наведені у таблиці

Вариант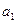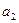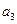
			-13
			-38
			-16
	-3	-9	-5
	-9		-20
	-6		-5
	-6		-13
	-12		-54
		-9	-27
	-3		-38
			-31
	-9		-28
		-3	-14
	-6		-4
	-12		-31
		-15	-52
	-6		-63
	-9
	-3	-3	-4
	-9		-28
	-6		-52

Обчислення значення полінома та його похідних у точці.

Означення

Поліномом(многочленом, багаточленом) степеня nназивається функція виду

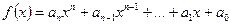, (1)

де 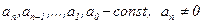, 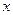- змінна, n –максимальний степінь входження змінної х з ненульовим коефіцієнтом у функцію.

Якщо коефіцієнти полінома є дійсними числами, то кажуть, що поліном заданий у множині 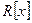. Якщо коефіцієнти комплексні, то – у множині .

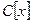Для уособлення функції поліном її часто позначають 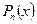, де n – показник степеня полінома.

Коренем полінома називається значення змінної 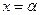, якщо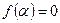

Основна теорема алгебри

Комплексний поліном степеня n > 0 має рівно n комплексних коренів, з урахуванням кратності.

Інакше кажучи, його можна розкласти на n лінійних множників

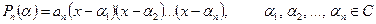- корені полінома. (2)

Якщо 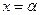є коренем полінома, то 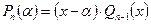, тобто поліном 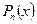без остачі ділиться на біном 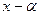. Поліном 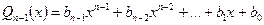носить назву частка від ділення 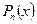на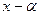

В разі, коли деяке значення змінної 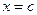не є коренем полінома, ділення полінома приймає вигляд

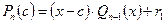, (3)

де 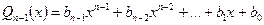- неповна частка від ділення 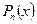на ,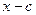

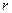– число, остача від ділення 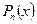на , .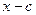

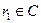Розглянемо (3) більш докладно.

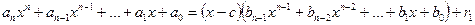(4)

Для обчислення значення поліному у точці 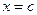достатньо підставити це значення у поліном. З правої частини (4) видно, що .

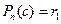Отже, значення полінома в довільній точці 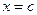дорівнює остачі від ділення полінома 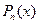на біном .

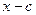Для знаходження остачі 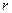і коефіцієнтів поліному 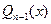розкриємо дужки у (4) і прирівняємо коефіцієнти при рівних степенях у правій і лівій частинах рівності.

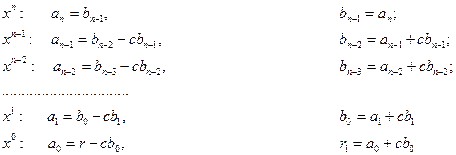
Схематично такі розрахунки записуються у вигляді схеми Горнера

				…

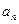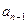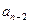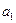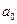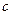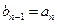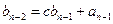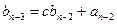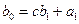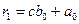Приклад 1

Обчислити значення полінома 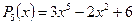в точці .

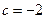Розв’язання.

Маємо поліном п’ятого степеня. Коефіцієнти полінома є такими:

.

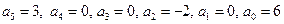Складемо схему Горнера ділення 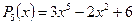на біном :

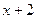				-2
-2		(-2)·3+0=-6	(-2)·(-6)+0=12	(-2)·12+(-2)=-26	(-2)·(-26)+0=52	(-2)·52+6=-98

Отже,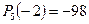

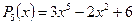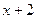Неповна частка від ділення на буде

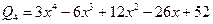
Отже можна записати