Решение типовых задач по расчету устойчивости стержней. Задания для индивидуальной работы
Пример 10.1. Расчет допускаемой нагрузки. Определить величину допускаемой сжимающей нагрузки для стойки с шарнирным закреплением концов (рис. 10.7, а) и прямоугольной формой поперечного сечения (рис. 10.7, б). Материал стойки Ст.3 с допускаемым напряжением на сжатие 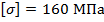 и запасом устойчивости
и запасом устойчивости 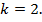
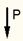 |
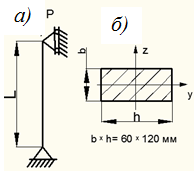
Рисунок 10.7 – Стойка при продольном изгибе
Решение
Данные задачи рекомендуется проводить в такой последовательности:
1. Определим площадь поперечного сечения стойки:
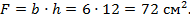
2. Рассчитаем величину минимального момента инерции сечения стойки (10.3):
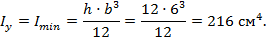
3. Вычислим минимальный радиус поперечного сечения по формуле (10.8):
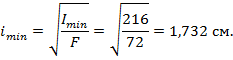
4. Найдем гибкость стойки (10.7), приняв коэффициент приведенной длины для граничных условий стойки 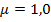 (см. рис. 10.5, а):
(см. рис. 10.5, а):
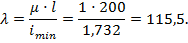
Так как гибкость стойки больше предельной гибкости для стального материала 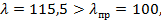 то опасную сжимающую силу можно рассчитать по формуле Эйлера (10.5):
то опасную сжимающую силу можно рассчитать по формуле Эйлера (10.5):
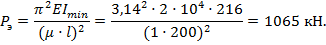
5. Величину допускаемой сжимающей нагрузки для стойки можно получить, разделив значения эйлеровой силы на заданный коэффициент запаса устойчивости:
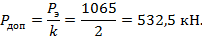
Таким образом, в работе стойки величину сжимающей нагрузки не следует допускать более 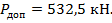
Величину допускаемой нагрузки можно определить и с использованием коэффициента уменьшения допускаемых напряжений на сжатие 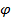 :
:
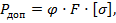
где коэффициент 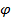 в зависимости от величины гибкости λ и материала (сталь с
в зависимости от величины гибкости λ и материала (сталь с 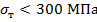 ) принимается равным
) принимается равным 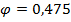 (используется интерполяция значений табл. 10.1).
(используется интерполяция значений табл. 10.1).
Тогда
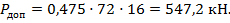
Как видно из расчетов, величины допускаемых нагрузок получились близкими, что вполне приемлемо для практических расчетов.
Пример 10.2. Расчет допускаемой нагрузки. Определить допускаемую сжимающую силу для стержня из стали Ст.3 длиной 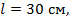 диаметром стержня
диаметром стержня 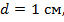 если верхний конец стержня шарнирно оперт, а нижний защемлен. Допускаемое напряжение на сжатие
если верхний конец стержня шарнирно оперт, а нижний защемлен. Допускаемое напряжение на сжатие 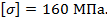 Коэффициент запаса прочности
Коэффициент запаса прочности 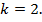
Решение
1. Вычислим площадь поперечного сечения стержня:
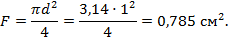
2. Определим момент инерции сечения относительно центральных осей:
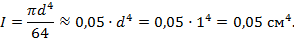
3. Рассчитаем радиус инерции сечения стержня:
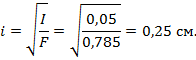
4. Определим гибкость стержня, приняв коэффициент приведенной длины стержня  (см. рис. 10.5, в):
(см. рис. 10.5, в):
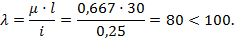
Следовательно, для этого стержня допускаемую силу нельзя определять по формуле Эйлера. Определим ее, пользуясь таблицей коэффициентов 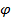 (см. табл.10.1): для данной гибкости
(см. табл.10.1): для данной гибкости 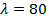 и материала стержня (сталь с
и материала стержня (сталь с 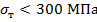 ) коэффициент уменьшения допускаемых напряжений
) коэффициент уменьшения допускаемых напряжений 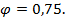
Тогда допускаемое напряжение на продольный изгиб стержня будет равен:
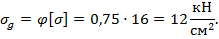
5. Допускаемая сила при сжатии стержня равна:
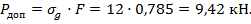
Величину допускаемой нагрузки можно определить, воспользовавшись формулой Ясинского (10.11), которая применяется при потере устойчивости стержня за пределом упругости. Приняв в этой формуле (см.п.10.3) 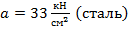 ;
; 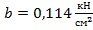 ;
; 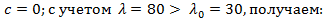
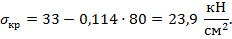
Тогда допускаемая нагрузка при сжатии стержня будет равна:
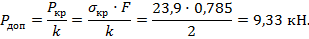
Полученный результат практически совпадает с предыдущим решением 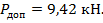
Пример 10.3. Подбор сечения стержня. Подобрать сечение стальной двутавровой стойки (рис.10.8, а) длиной 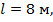 которая сжимается силой
которая сжимается силой 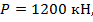 если допускаемое напряжение сжатия
если допускаемое напряжение сжатия 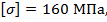 материал стойки сталь Ст.3.
материал стойки сталь Ст.3.
Решение
1. Требуемая площадь поперечного сечения стойки определяется по формуле:
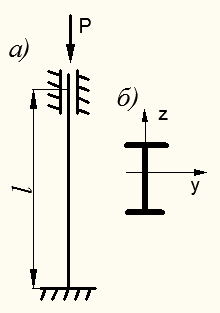
Рисунок 10.8 – Двутавровая стойка,
подверженная сжатию
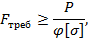
где 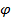 – коэффициент уменьшения допускаемого напряжения, который неизвестен и его предварительно можно принять
– коэффициент уменьшения допускаемого напряжения, который неизвестен и его предварительно можно принять 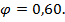
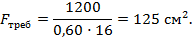
2. По таблице сортамента выбираем ближайший номер двутавра - №60, площадь сечения которого 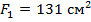 , минимальный радиус инерции сечения
, минимальный радиус инерции сечения 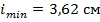 (выпучивание стойки происходит в направлении оси y, так как момент инерции сечения относительно этой оси
(выпучивание стойки происходит в направлении оси y, так как момент инерции сечения относительно этой оси 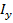 значительно меньше момента инерции
значительно меньше момента инерции 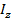 – см. рис. 10.8, б).
– см. рис. 10.8, б).
Для выбранного двутавра при 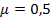 определим (см. рис. 10.5, г):
определим (см. рис. 10.5, г):
- гибкость стойки
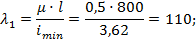
- коэффициент уменьшения допускаемого напряжения (см.табл.10.1) 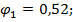
- допускаемое напряжение при продольном изгибе
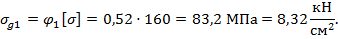
3. Рассчитаем сжимающее напряжение в стойке:
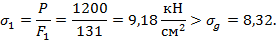
Следовательно, устойчивость стойки не обеспечена и необходимо принять новый номер двутавра: двутавр №65, 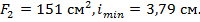
4. Определяем новые показатели принятого двутавра №65:
- гибкость стойки
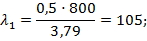
- коэффициент 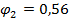 (см. табл.10.1);
(см. табл.10.1);
- допускаемое напряжение
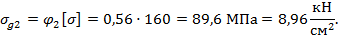
5. Рассчитаем новые сжимающие напряжения для выбранного двутавра:
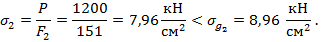
Стойка оказалась недогруженной на 11,2%, но с этим придется согласится, так как ближайший меньший двутавр, как было установлено, недостаточен.
