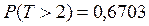Основные характеристики простейшего потока

ПРОСТЕЙШИЙ ПОТОК СОБЫТИЙ

Методические указания к практическим занятиям

по дисциплине «Высшая математика»

Составители: Ю.Б. Егорова

И.М. Мамонов

МОСКВА 2009

Егорова Ю.Б., Мамонов И.М. Простейший поток событий:Методические указания к практическим занятиямпо дисциплине «Высшая математика»/ Ю.Б. Егорова, И.М. Мамонов. М.: МАТИ, 2009. 16 с.

ÓЕгорова Ю.Б.,

Мамонов И.М.,

составление, 2009

Ó МАТИ, 2009

ВВЕДЕНИЕ

Методические указания предназначены для студентов дневного и вечернего отделений факультета №14 специальностей 150601, 160301, 230102. Методические указания служат основой для практических занятий и выполнения индивидуальных заданий.

ОСНОВНЫЕ ПОНЯТИЯ

1.1.Потоком событийназывается последовательность однородных событий, которые наступают в случайные моменты времени.

Примеры потоков:поступление вызовов на АТС или на пункт скорой помощи; прибытие самолетов в аэропорт; прибытие автомобилей на автозаправочную станцию; последовательность отказов элементов, ЭВМ, устройств; поток покупателей, пассажиров и т.п.

1.2. Простейшим (пуассоновским, стационарным) потокомназывается поток событий, который обладает тремя свойствами: стационарностью, «отсутствием последействия», ординарностью.

Поток называется стационарным, если его вероятностные характеристики не зависят от времени.

ПРИМЕР 1.Поток автомобилей в течение суток нестационарный, но в определенный промежуток времени (например, в час пик) поток становится стационарным, так как среднее число автомобилей в единицу времени приблизительно постоянен.

Поток называется потоком «без последействия», если число событий в одном промежутке времени не зависит от числа событий, наступивших в другом промежутке времени.

ПРИМЕР 2.Поток пассажиров, входящих в метро днем, не зависит от того, сколько вошло ночью. Поток покупателей, отходящих от прилавка, имеет последействие, так как зависит от времени обслуживания каждого покупателя.

Поток называется ординарным, если появление двух и более событий за малый промежуток времени практически невозможен, т.е. если события появляются в потоке поодиночке, а не группами.

ПРИМЕР 3.Поток поездов, подходящих к платформе - ординарен, а поток вагонов – неординарен.

основные характеристики простейшего потока

2.1.Простейший поток можно охарактеризовать двумя случайными величинами: числом событий, наступивших за определенное время, и временем между двумя последовательными событиями.

2.2. Дискретная случайная величина Х – число событий, наступивших за определенное время τ, - имеет закон распределения Пуассона. ДСВ Х принимает значения 0, 1, 2,…, m,…, ncвероятностями:

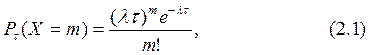
где λ -интенсивность потока - среднее число событий, которые появляются в единицу времени τ; λτ – параметр распределения Пуассона; m= 0, 1, 2,…,m, …n. Значения Р(Х=m) можно определить по таблицам распределения Пуассона в зависимости от λ_табл=λτ и m (см. Приложение) или подсчитать по формуле (2.1).

2.2.1.Ряд распределенияПуассона имеет вид:

X			…	m	…	n
P	е-l	lе-l	…		…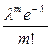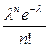

2.2.2.Согласно таблице можно записать функцию распределения случайной величины,распределенной по закону Пуассона:

F(х) = 0 , хЈ0;

;

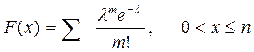F(х)=1, x>n.

2.2.3. Mатематическое ожидание и дисперсия случайной величины Х, распределенной по закону Пуассона, совпадают и равны параметру λτ этого закона:

M(X)= D(Х)=λτ.

2.3.Непрерывная случайная величина Т – время между двумя последовательными событиями простейшего потока - имеет показательный закон распределения.

2.3.1. Плотность распределения вероятностей (дифференциальная функция распределения)имеет вид:

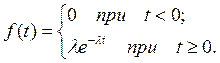
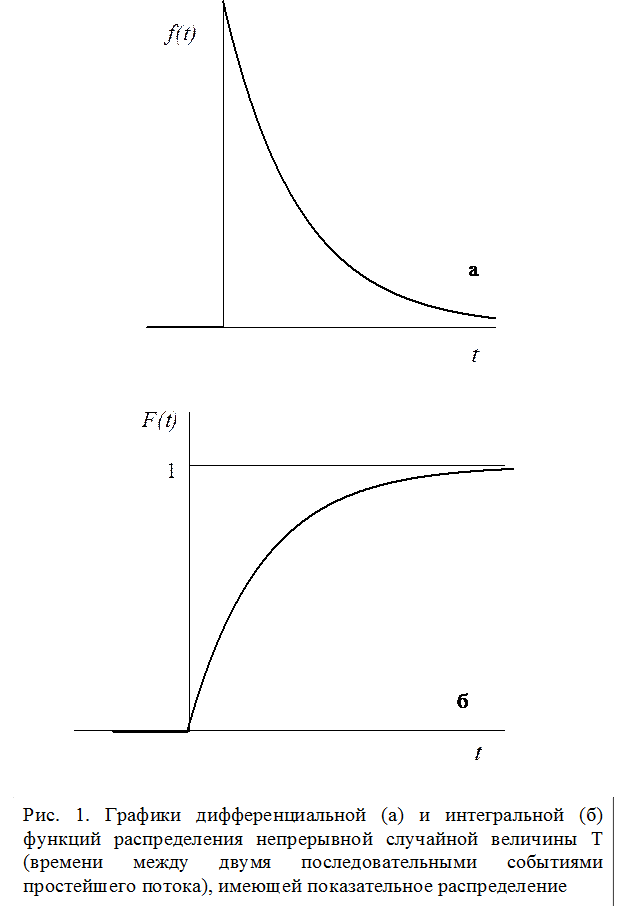
График функции f(t)приведен на рис.1, а.

2.3.2. Интегральная функция распределениявероятностей имеет вид:

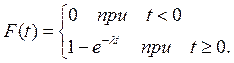
График функции F(t)приведен на рис. 1, б.

2.3.3. Числовые характеристикислучайной величины Т:

Mатематическое ожидание и среднее квадратическое отклонениесовпадают:

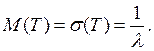
Дисперсия:

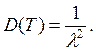
МодаМо=0.

Медиана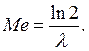

Коэффициент ассиметрииА=2.

Коэффициент эксцессаe=9, эксцесс Е=e–3=6.

ПРИМЕР 4.На АТС поступает простейший поток вызовов с интенсивностьюλ=0,2 вызова в секунду. а) Составить закон распределения числа вызовов в секунду. Найти числовые характеристики. б) Составить закон распределения времени ожидания вызова. Найти числовые характеристики. в) Чему равно среднее время ожидания вызова? г) Определить вероятность того, что за две секунды: не произойдет ни одного вызова; произойдет один вызов; хотя бы один вызов. д) Определить вероятность того, что время ожидания вызова превысит 2 секунды. Проиллюстрировать решение задачи графически.

Решение.

а) Дискретная случайная величина Х -число вызовов в секунду имеетзакон распределения Пуассона с параметром λτ=0,2·1=0,2 вызова. Способы задания закона распределения дискретной случайной величины – это ряд распределения, многоугольник распределения, функция распределения.

Значения Р(Х=m) найдем по таблице распределения Пуассона в зависимости от λ_табл=λτ=0,2 и m=1, 2, 3, … (см. Приложение). Тогда ряд распределения имеет вид:

X
P	0,8187	0,1638	0,0164	0,0010	0,0001	0,000..	0,000…

На основе ряда распределения построим многоугольник распределения (рис. 2, а) и найдем функцию распределения:

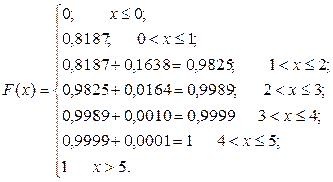
График F(x) приведен на рис. 2, б.

Числовые характеристики:

M(X)= λτ=0,2 вызова;

D(Х)=λτ= 0,2 (вызова)²;

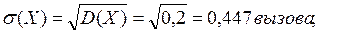
Мо=0 вызовов.

б) Непрерывная случайная величина Т – время ожидания вызова - имеет показательный закон распределения с параметром λ. Способы задания закона распределения непрерывной случайной величины – это дифференциальная и интегральная функции распределения вероятностей.

		Р
		х , вызовов
		х , вызовов
	Рис. 2. Многоугольник распределения (а) и функция распределения (б) дискретной случайной величины Х (числа вызовов), имеющей закон распределения Пуассона

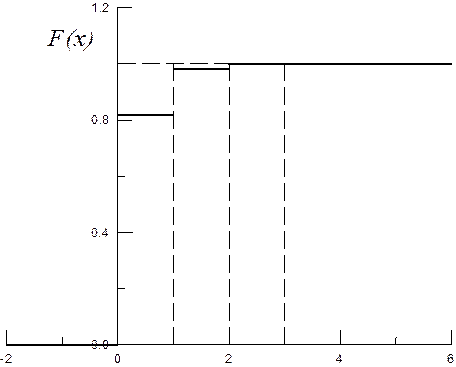
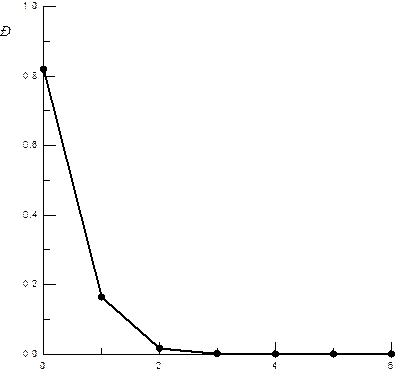
Плотность распределения вероятностей (дифференциальная функция распределения) имеет вид:

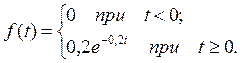
Интегральная функция распределения вероятностей имеет вид:

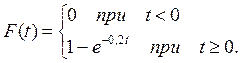
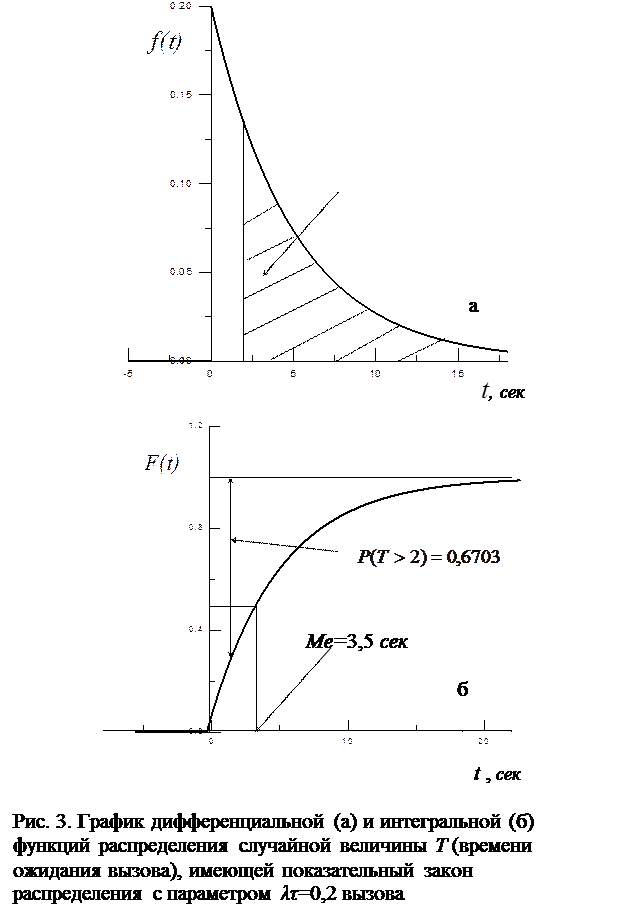
Графики функций f(t)и F(t)приведены на рис. 3.

Числовые характеристики случайной величины Т:

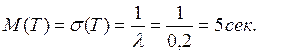
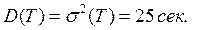
Мо=0 сек.

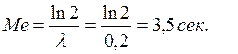
А=2.

e=9, Е=e–3=6.

в) Среднее время ожидания вызова равно математическому ожиданию М(Т)=5 сек.

г) Вероятность того, что за две секунды не произойдет ни одного вызова (m=0 ; τ=2 сек ) и один вызов (m=1 ; τ=2 сек ) можно определить по формуле (2.1):

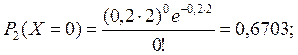
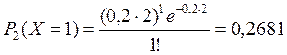
или по таблице распределения Пуассона в зависимости от λ_табл=λτ=0,2·2=0,4; m=0; m=1 (см. Приложение).

Вероятность того, что за две секунды произойдет хотя бы один вызов (т.е. или один, или два, или более вызовов), найдем с помощью теоремы сложения вероятностей противоположных событий:

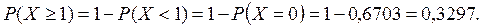
д) Определим вероятность того, что время ожидания вызова превысит 2 секунды:

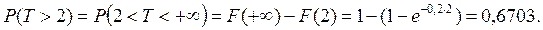
На графике f(t)(рис. 3, а)заштрихованная площадь численно равна 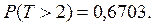На графике F(t)(рис. 3, б)искомая вероятность численно равна отрезку, выделенному стрелками.