Окружности (Curve - Circle)
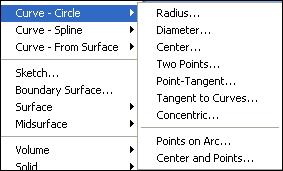Построение окружностей по методу Radius достаточно подробно было рассмотрено в первой работе.
По остальным возможностям приводится краткая сводка.
Radius – по центру и точке на окружности;
Diameter – по двум противоположным точкам на окружности;
Center – по центру и радиусу;
Two Points – по двум точкам и радиусу;
Point-Tangent – по центру и касательной;
Tangent to Curves – по касательной к двум линиям;
Concentric – окружность, концентрическая к ранее построенной окружности;
Points on Arc – пространственная окружность по трем точкам;
Center and Points ‑ пространственная окружность по центру и двум точкам.
Сплайны (Curve - Spline)
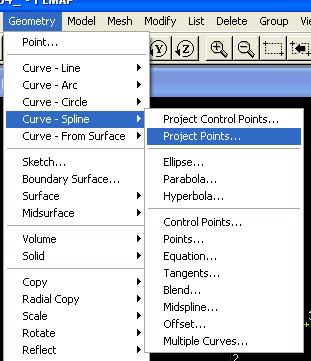Сплайны используются для построения линий, которые не являются ни прямыми, ни дугами окружностей. Сплайны состоят из кусков парабол, обычно кубических, которые подбираются таким образом, чтобы эти куски парабол в точках соединения имели общую касательную.
Для применения, по крайней мере в начале, рекомендуются методы Project Points для плоских сплайнов и Points для пространственных. Применение других методов требует несколько больших сведений о сплайнах, чем сведения, содержащиеся в предыдущем абзаце.
Проведем сплайн через точки 1, 6, 4, 5, используя метод Project Points.
В появившемся окне укажите точку 1 и нажмите ОК.
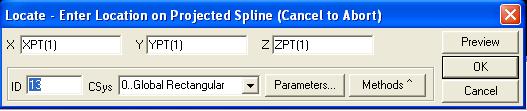
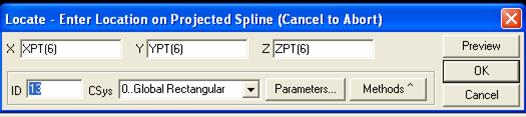
Вновь появляется такое же окно. Укажите в нем точку 6 и вновь ОК. Точки 1 и 6 соединятся прямой белой линией. Это еще не сплайн, а его черновой набросок.
 |
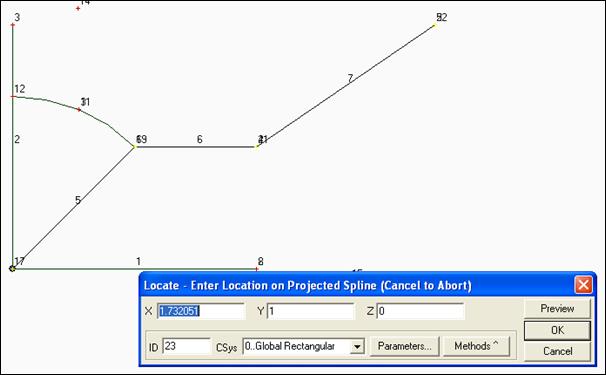Точно также поступите с точками 4 и 5. После указания последней точки картинка приобретет следующий вид.
Ломаная белая линия (белая на экране, а на рисунке, в целях экономии тонера, черная) показывает нам порядок соединения точек в сплайне. Теперь, когда все точки соединены, можно нажать кнопку Cancel. Это послужит FEMAP’у командой построить сплайн.
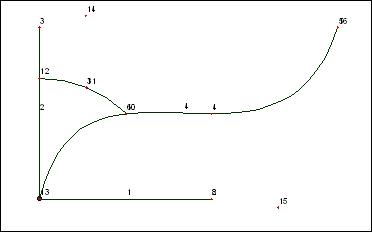Итоговая картинка будет иметь следующий вид:
Обратите внимание на то, что появились точки (на рисунке точки 14 и 15), которые вы не создавали. Это так называемые управляющие точки (Control Points), необходимые для определения касательных в крайних точках сплайна.
Метод Points применяется точно также, только используемые точки в общем случае могут не лежать в одной плоскости.
Замечание. Для построения сплайна следует указывать не менее четырех точек.
Краткая сводка команд построения сплайнов:
Плоские сплайны
Project Control Points – построение по управляющим точкам;
Project Points – построение по точкам, через которые должен проходить сплайн;
Канонические кривые
Ellipse – эллипс;
Parabola – парабола;
Hyperbola ‑ гипербола
Пространственные сплайны
Control Points –построение по управляющим точкам;
Points – построение по точкам, через которые должен проходить сплайн;
Equation – сплайн задается параметрическими уравнениями;
Tangents – сплайн задается касательными на краях;
Blend – соединение сплайном двух созданных ранее линий;
Midspline – сплайн лежащий посредине между двумя кривыми;
Offset – сплайн создается смещением точек ранее созданной кривой по нормали к ней на заданную величину;
Multiple Curves – объединяет несколько соединенных линий в одну линию (один объект)
Контрольные вопросы
В результате сегодняшнего занятия студент должен:
1. Знать какие системы координат можно использовать в FEMAP
2. Знать зачем могут понадобиться локальные системы координат, чем они отличаются от глобальных, и как их можно создавать?
3. Понимать, что такое рабочая плоскость и как можно управлять ее положением?
4. Знать, как построить точку, прямую, окружность, дугу окружности и сплайн.
Контрольные задания
При сдаче этой работы проверить усвоение материала можно только в режиме непосредственного диалога преподавателя и студента. То есть преподаватель задает вопросы по отдельным элементам диалоговых окон и предлагает построить какие-либо геометрические объекты.
Студент, усвоивший материал занятия, обязан четко знать назначение каждого элемента рассмотренных диалоговых окон, а также уверено и быстро строить рассмотренные геометрические объекты.