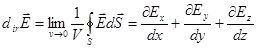Силовой линией электростатического поля называется линия, касательные к которой в каждой её точке совпадают по направлению с вектором напряжённости поля в той же точке
Из закона Кулона (2) и принципа суперпозиции (4) вытекает важное следствие -теорема Гаусса:
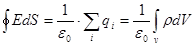 (5)
(5)
Здесь р - объёмная плотность заряда, распределённого в объёме V, ограниченном поверхностью S .
Применяя теорему (5) к бесконечно малому объёму Г-»0, можно получить соотношение между напряжённостью поля и объёмной плотностью заряда, выражающие теорему Гаусса в дифференциальной форме:
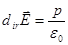 (6)
(6)
Величина, стоящая в левой части (6), называется дивергенцией вектора Ё и, по определению, равна:
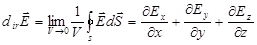
Ход работы:
| Циркуляция Г= 0,329(по расчётам) Циркуляция Г= 0 (теоретическое значение) Поток вектора напряжённости через поверхность призмы:12.39 Ф=12, 39. |
1 .Вычисление циркуляции вектора напряжённости электростатического поля по замкнутому контуру. Определение напряжённости электростатического поля по картине эквипотенциалей
| № | EA | 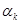 o o | 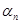 ° ° |
| 0,71 | |||
| 0,625 | |||
| 3 | 0,625 | ||
| 0,47 | |||
| 0,4 | |||
| 0,36 | |||
| 0,33 | |||
| 0,31 | |||
| 0,29 | |||
| 0,31 | |||
| 0,31 | |||
| 0,33 | |||
| 0.36 | |||
| 0.47 | |||
| 0.48 | |||
| 0.625 | |||
| 1.6 | |||
| 0,8 | |||
| 0,91 | |||
| 1.11 | |||
| 1.54 | |||
| 1.25 | |||
| 0.87 |
2.Определение линейной плотности заряда на проводнике.
Для определения линейной плотности заряда на проводнике используют теорему Гаусса:
| -12 |
| г = 117-10 |
З.Определение поверхностной плотности заряда на проводниках:
м 4. Определение ёмкости системы проводников:
С=117-1(Г12Ф
Контрольные вопросы:
1. Потенциалом электрического поля называется отношение потенциальной энергией,
которой обладает пробный заряд в данной точке к величине этого заряда.
Напряжённость Е - силовая характеристика электрического поля. Она показывает
значение силы, действующей на единичный заряд.
Все точки проводника в электростатическом поле имеют один и тот же потенциал,
напряжённость же поля внутри проводника равна нулю.
Напряжённость электростатического поля и его потенциал связаны между собой
соотношением:
, f^ тдф -г За» гдф
где §гааф=\ф = 1 —!-+j—:-+k—:- - градиент ^вектор, направленный в сторону ах ах oz
возрастания функции Ф (к, у, z) и численно равный изменению <р при перемещении на единицу длины в этом направлении.
2. Ё = J] Ё, - эта формула утверждает принцип суперпозиции полей. Если электрическое
поле создано системой зарядов, то напряжённость электрического поля, создаваемая этой системой равна векторной сумме напряжённостей, создаваемой в этой же точке.
3. Теорема Гаусса: поток вектора напряжённости электростатического поля в вакууме через произвольную замкнутую поверхность S равен алгебраической сумме заключённых внутри этой поверхности зарядов, делённой на е0:
\ *"""
- - ео v
4. Сущность метода моделирования электростатических полей заключается в следующем: заполним пространство между проводниками однородной слабопроводящей средой, а сами проводники будем рассматривать в качестве электродов, причём потенциалы проводников будем рассматривать постоянными. При этом в пространстве
между электродами возникает электрический ток, плотность которого j в любой точке определяется из закона Ома: j = АЁ ,где Л - удельная электропроводность среды, Ё -напряжённость электрического поля в данной точке.