Від’ємні числа у форматі байта

Від’ємні двійкові числа містять одиничний біт в старшому розряді і виражаються двійковим доповненням. Тобто, для подання від’ємного двійкового числа необхідно інвертувати всі біти і додати 1.

Розглянемо приклад:

Число 65: 01000001

Інверсія: 10111110

Плюс 1: 10111111 (рівно -65)

Якщо додати одиничні значення до числа 10111111, 65 не вийде.

Фактично двійкове число вважається від’ємним, якщо його старший біт рівний 1. Для визначення абсолютного значення від’ємного двійкового числа, необхідно повторити попередні операції: інвертувати всі біти і додати 1:

Двійкове значення: 10111111

Інверсія: 01000000

Плюс 1: 01000001 (рівно +65)

Сума +65 і -65 повинна скласти нуль:

01000001 (+65)

10111111 (-65)

(1) 00000000

Всі вісім біт мають нульове значення. Перенесення одиничного біта вліво втрачено. Проте, якщо було перенесення в знаковий розряд і з розрядної сітки, то результат є коректним.

Двійкове віднімання виконується просто: інвертується знак від'ємника і складаються два числа. Віднімемо, наприклад, 42 з 65. Двійкове подання для 42 є 00101010, і його двійкове доповнення: - 11010110:

65 01000001

+(-42) 11010110

23 (1) 00010111

Результат 23 є коректним. У розглянутому прикладі відбулося перенесення в знаковий розряд із розрядної сітки.

Якщо справедливість двійкового доповнення не відразу зрозуміла, розглянемо наступні задачі: Яке значення необхідно додати до двійкового числа 00000001, щоб одержати число 00000000? В термінах десяткового числення відповіддю буде -

1.

Для двійкового розглянемо 11111111:

Результат: (1) 00000000

Ігноруючи перенесення (1), можна бачити, що двійкове число 11111111 еквівалентно десятковому -1 і відповідно:

0 00000000

-(+1) -00000001

-1 11111111

Можна бачити також яким чином двійковими числами представлені

числа, що зменшуються:

+3 00000011

+2 00000010

+1 00000001

0 00000000

-1 11111111

-2 11111110

-3 11111101

Фактично нульові біти в від’ємному двійковому числі визначають його величину: розгляньте позиційні значення нульових бітів як якщо це були одиничні біти, складіть ці значення і додайте одиницю.

Порядок виконання роботи

1. Виконайте арифметичні операції у двійковій системі числення:

1.1. Знайдіть суму двох чисел 11001010 і 11011.

1.2. Знайдіть різницю двох чисел 11001010 і 11011.

1.3. Знайдіть добуток двох чисел 11001010 і 11011.

1.4. Знайдіть частку двох чисел 11001010 і 11011.

1.5. Знайдіть доповняльне число 11011.

2. Визначте двійкові доповнення для наступних двійкових чисел: а) 00010011, б) 00111100, в) 00111001.

3. Визначте абсолютні значення для наступних від’ємних двійкових чисел: а) 11001000, б) 10111101, в) 10000000.

Продемонструйте викладачу результати виконаної роботи.

5. Перевірте правильність виконання дій за допомогою калькулятора «Інженерний» стандартного офісного пакету MW.

6. Зверніться до викладача за індивідуальним завданням.

7. Підготуйте звіт відповідно встановленого зразку.

Контрольні запитання.

1. Які засоби стандартного офісного пакету Microsoft Windows 98/XP для виконання арифметичних дій у системах числення з основою 2, 8, 16?

2. Що називають доповняльним числом?

3. В чому полягає найважливіша перевага двійкової системи числення?

4. Яким чином подаються від’ємні числа у форматі байта?

5. Як знайти абсолютне значення від’ємного числа?

6. Яким чином виконується двійкове віднімання?

ЛАБОРАТОРНА РОБОТА № 6.

Тема:	Двійково-десяткова система числення.
Мета роботи: Зміст роботи: Організаційні та методичні вказівки:	Набуття практичних навичок перетворення двійкових чисел у двійково-десяткові. Закріплення навичок переведення чисел з двійково-десяткової системи числення у двійкову. Узагальнення та систематизація знань про системи числення, що застосовують в ЕОТ. Повторення правил переведення чисел з однієї системи числення в інші. Повторення теоретичних відомостей про системи числення та застосування навичок переведення чисел з однієї системи числення в іншу. Застосування засобів Microsoft Windows для виконання переведення чисел у двійкову, вісімкову та шістнадцяткову системи числення. Лабораторну роботу проводять після вивчення розділу “Системи числення” з підгрупою студентів в два етапи: 1. Підготовчий етап: Повторення теоретичних відомостей про системи числення. Дослідження алгоритмів переведення чисел з однієї системи числення в іншу з метою формування узагальненої моделі виконання відповідних дій. 2. Виконавчий етап: Виконання індивідуальних завдань та перевірка правильності виконаних дій засобами калькулятора «Інженерний» стандартного офісного пакету Microsoft Windows.
Технічне забезпечення:	Персональний комп’ютер, дискета.
Програмне забезпечення:	Windows XP, Advanced Grapher.
Час:	80 хвилин.

Теоретична частина

Наявність блоку десяткової арифметики в АЛП виключає при рішенні задач необхідність переводу чисел з однієї системи числення в іншу. Використання двох основних систем числення ( двійкової і двійково-десятковоі) дозволяє створювати ЕОМ надзвичайно високої потужності.

Десяткові числа двійково-десятковоі системи числення, яка використовується в ЕОМ в якості допоміжної, зазвичай кодується прямим двійковим кодом 8-4-2-1.

Десятковий код	Код 8-4-2-1	Код з залишком 6	Десятковий код	Код 8-4-2-1	Код з залишком 6

Для того щоб записати десяткове число в двійково-десятковому коді 8-4-2-1, необхідно кожну цифру десяткового числа замінити відповідною тетрадою.

Наприклад , користуючись таблицею, запишемо десяткове число

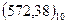в двійково-десятковому коді 8-4-2-1:

5 7 2 3 8

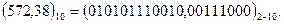
Для того щоб перевести число з двійково-десяткового коду 8-4-2-1 в десятковий, необхідно кожну тетраду двійково-десяткового числа замінити десятковим числом.

Наприклад, використовуючи таблицю, число 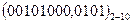, записане в коді 8-4-2-1, в десятковій системі числення буде мати такий вигляд:

2 8 5

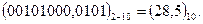
Перетворення чисел з десяткової системи числення в двійково-десяткову не пов’язані з обчисленнями і легко реалізуються за допомогою найпростіших електронних схем, так як перетворенню підлягає невелика кількість (чотири) двійкових цифр. Двійково-десяткові числа перетворюються в десяткові автоматично в ЕОМ за спеціальною програмою переведення.

Запишемо десяткове число 3691 у ДДК 8421. Кожна десяткова цифра перетвориться прямо у свій двійково-десятковий еквівалент із 4 біт, і перетворення дають 3691₁₀ = 0011 0110 1001 0001ддк :

Десяткове число
Двійково-десяткове число

Перетворимо тепер двійково-десяткове число 1000 0000 0111 0010 у його десятковий еквівалент. Кожна група з 4 біт прямо перетвориться в її десятковий еквівалент, і тоді одержуємо: 1000 0000 0111 0010_ДДК = 8072₁₀:

Двійково-десяткове число
Десяткове число

В ЕОМ, в яких передбачена можливість виконання арифметичних операцій над десятковими числами при виконанні операцій десяткові числа з коду 8-4-2-1 перетворюються в залишковий код 6. Використання залишкових кодів дає можливість спростити діі з десятковими числами в АЛП, так як залишкові коди є самодоповнюючими, тобто інверсія його двійкових цифр дає доповнення до 9.

В ЕОМ 3-го та 4-го покоління використовується код з залишком 6, який дозволяє при додаванні автоматично проводити перенос в старші десяткові розряди.

Для показу службової інформації – програм для підготовки задач до рішення на ЕОМ – застосовують допоміжні системи числення – вісімкову і шістнадцяткову.

Вісімкова система числення має основу d=8 і а_і=0, 1, 2, 3, 4, 5, 6, 7.

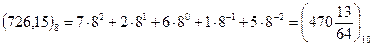Будь-яке вісімкове число може бути представлене за допомогою формули розкладання десятковим еквівалентом, наприклад:

Запис команд програми у вісімковій системі числення у три рази коротше, ніж в двійковій.

Шістнадцяткова система численнямає основу d=16 і а_і=0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. При такому зображенні цифр у шістнадцятковій системі числення буква А зображає десять, B – одинадцять, З – дванадцять, D – тринадцять, E – чотирнадцять, F – п'ятнадцять.

Будь-яке число з шістнадцяткової системи числення також може бути представлене десятковим числом за допомогою формули розкладання.

Шістнадцяткова система числення так само, як і вісімкова, використовується при складанні програм для коротшого і зручнішого запису двійкових кодів – команд. Крім того в деяких ЕОМ шістнадцяткова система числення застосовується для представлення чисел в напівлогарифмічній формі.