Теорема.Элементар түрлендірулер матрица рангісін өзгертпейді. 4 страница

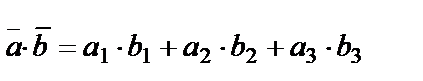
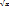Вектордың ұзындығының формуласы: АВ = ²+ ²+ ²

Вектор деп бағытталған кесіндіні атаймыз. Яғни AB вектордың A басы мен B ұшы бар болады:

В

А+В

А

МысалыD(5; 4)

3CD

1 С(1;1)

1 2 3 4 5

Вектордың басы мен ұшының арақашықтығы оның (вектордың) ұзындығы немесе абсолюттік шамасы деп аталады.

Мысалы жоғарыдағы CD векторының |CD| ұзындығы:

CD|= 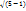²+(4-1)²

|CD|= 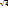²+3²

|CD|=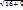

|CD|=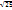

|CD|=5

Егер вектордың басы мен ұшы бір нүктеде орналасса онда бұндай векторды нөлдік вектор деп атайды. Өйткені бұндай вектордың ұзындығы нөлге тең.

Вектордың координаттары деп оның (вектордың) ұшының және басының сәйкесінше координаттарының айырмасын атаймыз.

Яғни AB векторының басы A(x₁, y₁) нүктесі ал ұшы B(x₂, y₂) нүктесі болса онда AB векторының координаттары (x₂-x₁, y₂ –y₁) болады.

Мысалы жоғарыдағы CD векторының координаттары (5-1; 4-1)=(4; 3).

Геометрияда сәйкесінше координаттары бірдей векторларды бірдей векторлар деп санайды.

Соңдықтан векторларды a, b, c,… деп бір ғана әріппен белгілейміз. a векторының координаттарын (a_Х, a_У) деп белгілейміз. Ал a векторының өзін кейде {a_Х, a_У} деп те белгілейміз

25. Вектордың орты.Өзінің сандық мәнімен қоса кеңістіктегі бағытымен де сипатталатын шамалар векторлық шамалар немесе векторлар деп аталады.

Сонымен, орын ауыстыру векторлық шама болып табылады. Векторларды бағытталған кесінді түрінде кескіндейді және бір әріппен немесе вектордың басы мен ұшын көрсететін екі әріппен белгілеп, төбесіне нұскама (стрелка) қояды. Мысалы жылдамдық векторын ʋ немесе АВ, күш векторын F немесе CD түрінде кескіндеуге болады.

Кеңістікте белгілі бір бағыты болмайтын, тек сандық мәнімен ғана сипатталатын шаталар скалярлық шамалар немесе скалярлар деп аталады. Мысалы, уақыт, заттың тығыздығы, дененің көлемі, температура, арақашықтығын (орын ауыстыру емес), сынып бөлмесінің ұзындығы, ені және биіктігі, т.с.с. скалярлық шамаларға жатады.

Кез келген вектордың сандық мәні оның модулі деп аталады.Модуль — скалярлық шама.

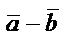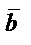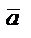Егер a және b векторларының модульдері мен бағыттары бірдей болса, онда олар тең болады а = b. Ал векторлардың модульдері тең болып, бірақ бағыттары қарама-қарсы болса, онда а = - b болады.

Берілген а векторын кез келген k скалярға көбейту (бөлу) үшін осы вектордың модулін берілген санға көбейтеміз (бөлеміз): b = k • a (b = a :k). Қорытқы b вектордың бағыты k көбейткішінің (бөлгішінің) таңбасымен анықталады. Егер k оң болса (k > 0), онда b векторы а векторымен бағыттас, ал k теріс болса (k < 0), b векторының бағыты а векторының бағытына қарама-қарсы болады.Ұзындығы бірге тең векторды бірлік вектор деп атайды және оны е деп белгілейді. Егер бірлік векторының бағыты а векторының бағытымен сәйкес келсе онда ол а векторының орты деп аталады.

Коллинеар векторлар.

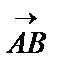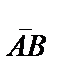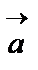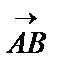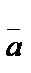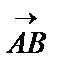Басы А, соңы В нүктесі болатын бағытталған кесінді вектор деп аталады. Оқулықтарда векторларды немесе , кейде тек қалың әріптермен АВ белгілеу түрлері кездеседі. Сол сияқты векторларды бір әріппен де белгілей береді ( = , , а). векторының ұзындығы деп АВ кесіндісінің ұзындығын айтады және 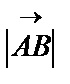деп белгілейді. Басы мен соңы беттесетін вектор нолдік вектор деп аталады, 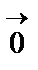= 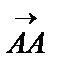және ұзындығы нолге тең.Бір түзудің не өзара параллель түзулер бойында орналасқан векторлар коллениар векторлар деп аталады. 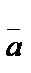және 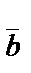векторларының қосындысы «үшбұрыш» не «параллелограмм» ережесімен анықталады:

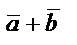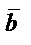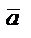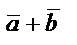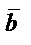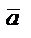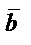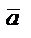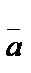және 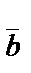векторларының 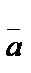- 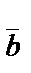айырымы деп 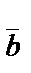-ға қосқанда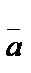

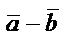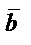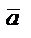векторы алынатын 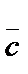= 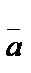- 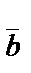векторын айтады.

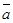|| болғандықтан оны 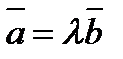деп жазуға болады, мұндағы 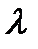- қайсыбір сан. Осыдан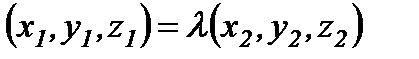 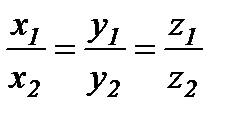-екі вектордың коллинеарлығының белгісі.

27. Компланар векторлар.Векторлардың компланарлық шарты а, в, с векторлардың бас нүктелерін бір нүктеге түйістіргенде олар бір жазықтықта орналасса онда ол векторлар компланар болады. Белгісі: а = в + с. Егер векторлар координаталарымен берілсе, яғни а (х1, у1, Z1), в (х2, у2, Z2), с (х3, у3, Z3) болса, онда олардың компланарлық белгісі:

х1 у1 Z1

х2 у2 Z2 = 0

х3 у3 Z3

Мысалдар: 1) а = i – j + 2, в= 3i +j,

c= mi + 2kвекторлары компланар болатындай m мәнін тап.

1 - 1 2

3 1 0 = 2 - 2m + 6 = 0 = m = 4, = а = gв + pс орындала ма, тексерейік; а (1; -1, 2) = g (3,

M0 2 1, 0) + р (4, 0, 2) = 1 = 3g + 4р

-1 = g + 0 =

2 = 0 + 2р

= g = -1 = а = -в + с, яғни векторлар компланар.

р = 1

Үш вектордың компланар бояу шарты

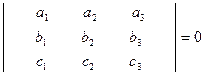(42)

формуламен, ал 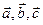векторлар қыры болатын параллепипед көлемi.

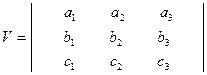(43)

формуламен, ал бiр төбеден шығатын қырлары 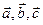болатын тетраэдрдiң көлемi.

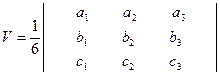(44)

формуламен табылады.