Оэффициент корреляции (см фото1)

Свойства коэффициента корреляции r

· r изменяется в интервале от —1 до +1.

· Знак r означает, увеличивается ли одна переменная по мере того, как увеличивается другая (положительный r), или уменьшается ли одна переменная по мере того, как увеличивается другая (отрицательный r).

· Величина r величина указывает, как близко расположены точки к прямой линии. В частности, если r = +1 или r= —1, то имеется абсолютная (функциональная) корреляция по всем точкам, лежащим на линии (практически это маловероятно); если 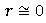, то линейной корреляции нет (хотя может быть нелинейное соотношение). Чем ближе r к крайним точкам (±1), тем больше степень линейной связи.

· Коэффициент корреляции r безразмерен, т. е. не имеет единиц измерения.

· Величина r обоснованна только в диапазоне значений x и y в выборке. Нельзя заключить, что он будет иметь ту же величину при рассмотрении значений x или y, которые значительно больше, чем их значения в выборке.

· x и y могут взаимозаменяться, не влияя на величину r ( ).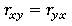

· Корреляция между x и у не обязательно означает соотношение причины и следствия.

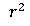· представляет собой долю вариабельности у, которая обусловлена линейным соотношением с x.

Статистическая значимость коэффициента корреляции

l Если коэффициент корреляции вычислен на основе выборочных данных, то не исключено, что его ненулевое значение является не отражением действительной связи между признаками, а просто получено в результате специфики данной выборки (тогда как в генеральной совокупности коэффициент корреляции равен нулю, т.е. линейной связи между признаками нет).

l Таким образом, надо понять, как далеко значение r от нуля.

l Если значение коэффициента корреляции вычислено по выборочным данным, то для оценки его значения в генеральной совокупности, как обычно, строится доверительный интервал.

l Для построения доверительного интервала вычисляется ошибка коэффициента корреляции sr по формуле:

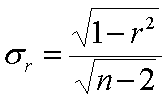
l Затем ошибка коэффициента корреляции умножается на параметр t, зависящий от доверительной вероятности P ( для вероятности 95% t = 2), чтобы найти предельную ошибку.

l Наконец, строится доверительный интервал r ± σr и проводится проверка, попадет ли нулевое значение в этот интервал.

l Если ноль не попадет в доверительный интервал, значит с высокой вероятностью в генеральной совокупности не может быть нулевого значения коэффициента корреляции, т.е. связь между признаками существует и в генеральной совокупности. В таком случае коэффициент корреляции является статистически значимым.

l -1 0 r 1

l

l Если ноль попадет в доверительный интервал, значит с высокой вероятностью в генеральной совокупности может оказаться нулевая корреляция, т.е. отсутствие связи. В таком случае коэффициент корреляции является статистически незначимым.

l -1 0 r 1

l Значимые коэффициенты в программе Statistica показаны красным цветом, незначимые – черным. Незначимые коэффициенты можно считать нулями и принимать во внимание только значимые.

l

l Необходимо подчеркнуть, что величина коэффициента корреляции еще не гарантирует его значимости: даже большой коэффициент может оказаться статистически незначимым (например, при малом объеме выборки), а небольшой коэффициент (если выборка велика) – значимым.

29?. Основная особенность регрессионного анализа: при его помощи можно получить конкретные сведения о том, какую форму и характер имеет зависимость между исследуемыми переменными.

Задачи регрессионного анализа

Рассмотрим основные задачи регрессионного анализа: установление формы зависимости, определение функции регрессии, оценка неизвестных значений зависимой переменной.

Установление формы зависимости.

Характер и форма зависимости между переменными могут образовывать следующие разновидности регрессии:

· положительная линейная регрессия (выражается в равномерном росте функции);

· положительная равноускоренно возрастающая регрессия;

· положительная равнозамедленно возрастающая регрессия;

· отрицательная линейная регрессия (выражается в равномерном падении функции);

· отрицательная равноускоренно убывающая регрессия;

· отрицательная равнозамедленно убывающая регрессия.

Однако описанные разновидности обычно встречаются не в чистом виде, а в сочетании друг с другом. В таком случае говорят о комбинированных формах регрессии.

Определение функции регрессии.

Вторая задача сводится к выяснению действия на зависимую переменную главных факторов или причин, при неизменных прочих равных условиях, и при условии исключения воздействия на зависимую переменную случайных элементов. Функция регрессии определяется в виде математического уравнения того или иного типа.

Оценка неизвестных значений зависимой переменной.

Решение этой задачи сводится к решению задачи одного из типов:

· Оценка значений зависимой переменной внутри рассматриваемого интервала исходных данных, т.е. пропущенных значений; при этом решается задача интерполяции.

· Оценка будущих значений зависимой переменной, т.е. нахождение значений вне заданного интервала исходных данных; при этом решается задача экстраполяции.

Обе задачи решаются путем подстановки в уравнение регрессии найденных оценок параметров значений независимых переменных. Результат решения уравнения представляет собой оценку значения целевой (зависимой) переменной.

Рассмотрим некоторые предположения, на которые опирается регрессионный анализ.

Предположение линейности, т.е. предполагается, что связь между рассматриваемыми переменными является линейной. Так, в рассматриваемом примере мы построили диаграмму рассеивания и смогли увидеть явную линейную связь. Если же на диаграмме рассеивания переменных мы видим явное отсутствие линейной связи, т.е. присутствует нелинейная связь, следует использовать нелинейные методы анализа.

Предположение о нормальности остатков. Оно допускает, что распределение разницы предсказанных и наблюдаемых значений является нормальным. Для визуального определения характера распределения можно воспользоваться гистограммами остатков.

При использовании регрессионного анализа следует учитывать его основное ограничение. Оно состоит в том, что регрессионный анализ позволяет обнаружить лишь зависимости, а не связи, лежащие в основе этих зависимостей.

Регрессионный анализ дает возможность оценить степень связи между переменными путем вычисления предполагаемого значения переменной на основании нескольких известных значений.

Линейная регрессия ( см фото2)

Множественная линейная регрессия

В общем случае в регрессионный анализ вовлекаются несколько независимых переменных. Это, конечно же, наносит ущерб наглядности получаемых результатов, так как подобные множественные связи в конце концов становится невозможно представить графически.

В случае множественного регрессионного анализа речь идёт необходимо оценить коэффициенты уравнения

у = b₁ -х₁ +b₂ -х₂ +... + b_n -х_n +а,

где n — количество независимых переменных, обозначенных как х₁ и х_n , а — некоторая константа.

Переменные, объявленные независимыми, могут сами коррелировать между собой; этот факт необходимо обязательно учитывать при определении коэффициентов уравнения регрессии для того, чтобы избежать ложных корреляций.