Всюду в указанных формулах через обозначается некоторая рациональная функция от переменных и ,т.е. , где - многочлены степеней и соответственно от переменных и .
Греческий алфавит
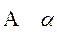 альфа alpha
альфа alpha
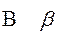 бета beta
бета beta
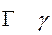 гамма gamma
гамма gamma
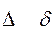 дельта delta
дельта delta
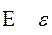 эпсилон epsilon
эпсилон epsilon
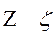 дзета zeta
дзета zeta
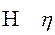 эта eta
эта eta
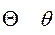 (или
(или 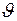 ) тета theta
) тета theta
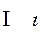 йота iota
йота iota
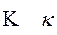 каппа kappa
каппа kappa
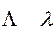 ламбда lambda
ламбда lambda
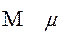 мю mu
мю mu
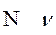 ню nu
ню nu
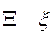 кси xi
кси xi
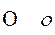 омикрон omicron
омикрон omicron
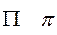 пи pi
пи pi
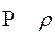 ро rho
ро rho
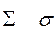 сигма sigma
сигма sigma
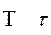 тау tau
тау tau
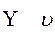 ипсилон upsilon
ипсилон upsilon
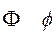 (или
(или 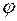 ) фи phi
) фи phi
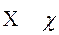 хи chi
хи chi
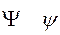 пси psi
пси psi
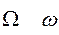 омега omega
омега omega
Эквивалентные функции
при 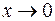
1. .
2. .
3. .
4. .
5. .
6. 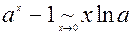 ,
, 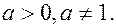
7. 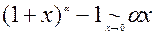 ,
, 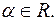
8. .
9. .
Где .
11. 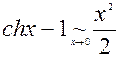
 где
где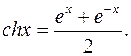
12. .
Сравнение функций. O(f) и o(f).
1. .
2. .
3. .
4. .
5. .
6. .
7. .
8. .
9. .
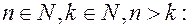
10. .
11. .
12. .
12. .
13. .
14. .
15. .
16. 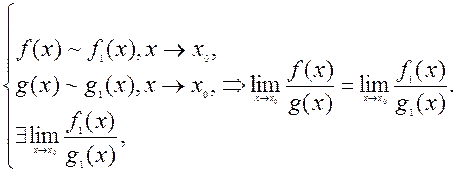
Таблица производных
1. 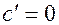 ,
, 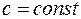
2. 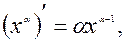
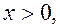
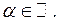
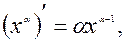
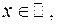
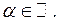
3. 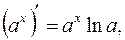
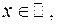
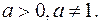
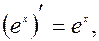
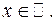
4. 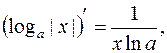
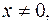
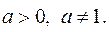
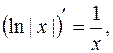
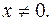
5. 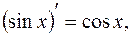
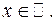
6. 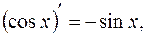
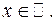
7. 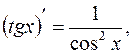
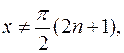
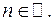
8. 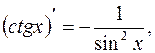
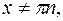
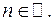
9. 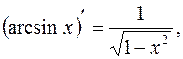
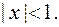
10. 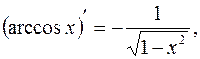
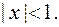
11. 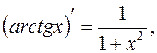
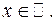
12. 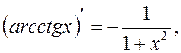
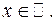
13. 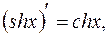
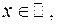 где
где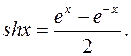
14. 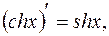
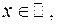 где
где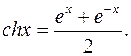
15. 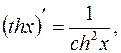
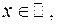
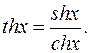
16. 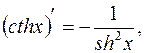
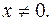
Производные высших порядков
1) 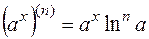 ,
, 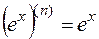 ;
;
2) 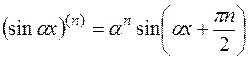 ;
;
3) 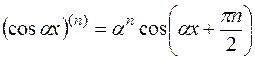 ;
;
4) 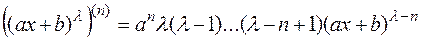 ;
;
5) 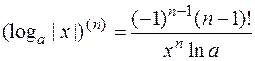 ,
, 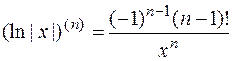 .
.
Если функции 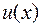 и
и 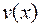 имеют производные порядка
имеют производные порядка 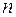 , то функции
, то функции 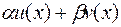 (
( 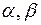 -постоянные) и
-постоянные) и 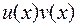 также имеют производные порядка
также имеют производные порядка 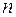 , причем
, причем
6) 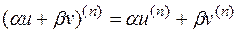 ;
;
7) 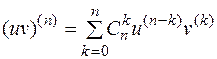 - формула Лейбница.
- формула Лейбница.
Формулы Маклорена для основных элементарных функций
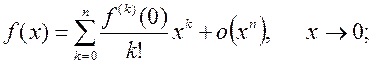
1. 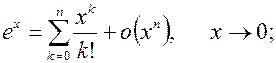
2. 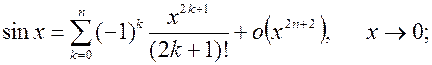
3. 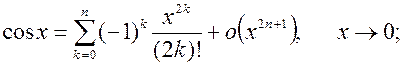
4. 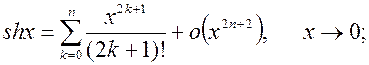 где
где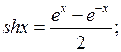
5. 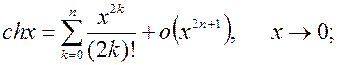 где
где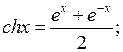
6. 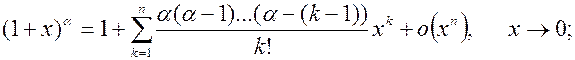
6.1. 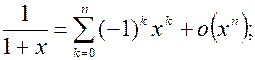
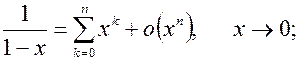
7. 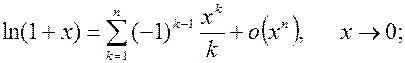
7.1. 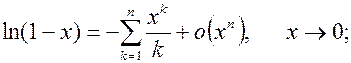
8. 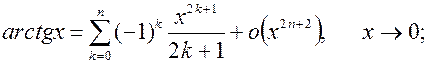
9. 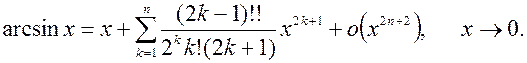
10. 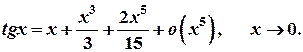
Если 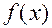 - четная функция, то:
- четная функция, то: 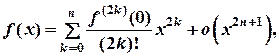
если 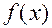 - нечетная функция, то:
- нечетная функция, то: 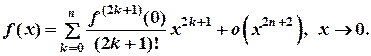
Исследование функций и построение графиков
1.Найти область определения функции.
2.Исследовать, не является ли функция четной или нечетной.
3.Исследовать, не является ли функция периодической.
4.Исследовать поведение функции в окрестности точек разрыва. Выписать вертикальные асимптоты.
5.Найти точки пересечения с осями координат и промежутки постоянства знака.
6.Найти горизонтальные и наклонные асимптоты.
7.Определить промежутки убывания и возрастания функции, а также точки экстремума.
8.Найти точки перегиба и установить промежутки выпуклости вверх и вниз графика функции.
9.Построить график функции.

Исследование функций и построение графиков
1.Найти область определения функции.
2.Исследовать, не является ли функция четной или нечетной.
3.Исследовать, не является ли функция периодической.
4.Исследовать поведение функции в окрестности точек разрыва. Выписать вертикальные асимптоты.
5.Найти точки пересечения с осями координат и промежутки постоянства знака.
6.Найти горизонтальные и наклонные асимптоты.
7.Определить промежутки убывания и возрастания функции, а также точки экстремума.
8.Найти точки перегиба и установить промежутки выпуклости вверх и вниз графика функции.
9.Построить график функции.
Таблица неопределенных интегралов
1. 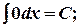 2.
2. 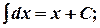
3. 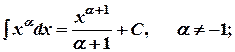
4. 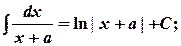
5. 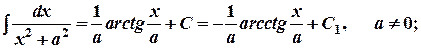
6. 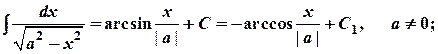
7. 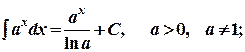
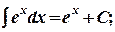
8. 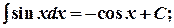 9.
9. 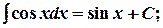
10. 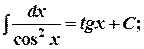
11. 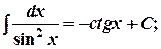
12. 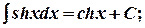 где
где 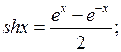
13. 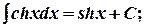 где
где 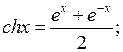
14. 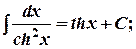
15. 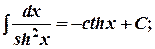
16. 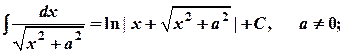
17. 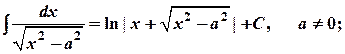
18. 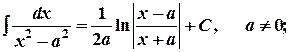
19. 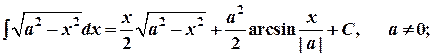
20. 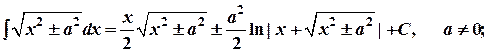
21. 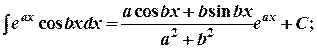
22. 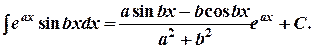
Интегралы, сводящиеся к интегралам от рациональных функций
Всюду в указанных формулах через обозначается некоторая рациональная функция от переменных и ,т.е. , где - многочлены степеней и соответственно от переменных и .
- Интегралы вида
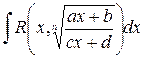 ,
, 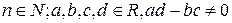 . (1)
. (1)
Положим 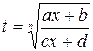 . Тогда
. Тогда 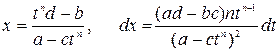 .
.
В силу формулы замены переменных в неопределённом интеграле
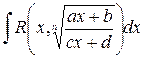 =
= 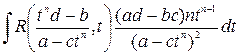 .
.
Т.о. вычисление интеграла вида (1) сводится к вычислению интеграла от рациональной функции переменной 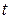 .
.
- Интегралы вида
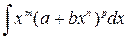 ,
, 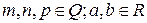 . (2)
. (2)
Выражение, стоящее под знаком интеграла, называется биномиальным дифференциалом.
П.Л. Чебышев доказал, что интегралы этого вида выражаются через элементарные функции лишь в трёх случаях:
1) 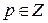 .
.
Пусть 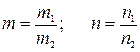 где
где 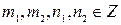 .
.
Положим 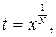 где
где 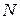 - наименьшее общее кратное чисел
- наименьшее общее кратное чисел 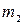 и
и 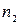 . Данная замена переменной сводит вычисление интеграла (2) к вычислению интеграла от рациональной функции переменной
. Данная замена переменной сводит вычисление интеграла (2) к вычислению интеграла от рациональной функции переменной 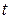 .
.
2) 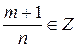 .
.
Пусть 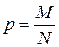 где
где 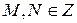 .
.
Положим 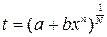 . Данная замена переменной приводит к вычислению интеграла от рациональной функции переменной
. Данная замена переменной приводит к вычислению интеграла от рациональной функции переменной 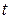 .
.
3) 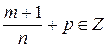 .
.
Пусть 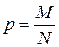 где
где 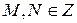 . Положим
. Положим 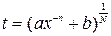 . Данная замена переменной приводит к вычислению интеграла от рациональной функции переменной
. Данная замена переменной приводит к вычислению интеграла от рациональной функции переменной 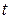 .
.
- Интегралы вида
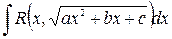 ,
, 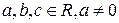 . (3)
. (3)
Для рационализации интегралов этого вида применяются подстановки Эйлера трех типов.
1)Если 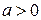 , то полагаем
, то полагаем
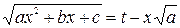 или
или 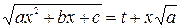 .
.
2)Если 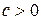 , то полагаем
, то полагаем
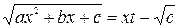 или
или 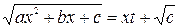 .
.
3)Если квадратный трехчлен 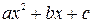 имеет различные вещественные корни
имеет различные вещественные корни 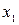 и
и 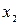 , то полагаем
, то полагаем
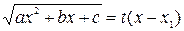 или
или 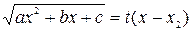 .
.
Подстановки Эйлера универсальны (т.е. применимы к любому интегралу указанного вида). Однако во многих случаях они приводят к неоправданно сложным рациональным функциям. Поэтому часто используют другие методы, основанные на элементарных преобразованиях.
Еще одна полезная формула, применимая к интегралам вида
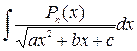 , где
, где 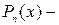 полином
полином 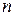 -й степени,
-й степени, 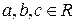 :
:
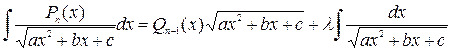 .
.
В этой формуле 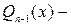 многочлен
многочлен 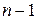 - й степени с неизвестными коэффициентами,
- й степени с неизвестными коэффициентами, 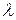 - неизвестный множитель. Для отыскания этих неизвестных величин указанное равенство дифференцируют, а результат после умножения на
- неизвестный множитель. Для отыскания этих неизвестных величин указанное равенство дифференцируют, а результат после умножения на 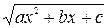 и приравнивания коэффициентов при соответствующих степенях
и приравнивания коэффициентов при соответствующих степенях 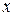 дает систему уравнений для отыскания коэффициентов многочлена
дает систему уравнений для отыскания коэффициентов многочлена 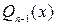 и множителя
и множителя 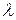 .
.
- Интегралы вида
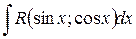 (4)
(4)
всегда рационализируются универсальнойподстановкой
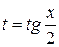 . Тогда
. Тогда 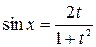 ,
, 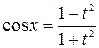 ,
, 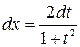 .
.
Специальные случаи:
1)Если 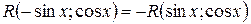 , то полагаем
, то полагаем 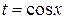 .
.
2)Если 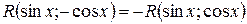 , то полагаем
, то полагаем 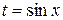 .
.
3)Если 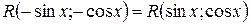 , то полагаем
, то полагаем 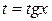 или
или 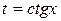 .
.
Иногда удобно преобразовывать подинтегральную функцию, имеющую вид произведения синусов и косинусов (или их степеней), в сумму, пользуясь формулами понижения степени или другими тригонометрическими формулами.
- Интегралы вида
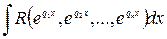 ,
, 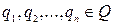 (5)
(5)
рационализируются при помощи подстановки 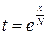 , где
, где 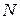 - наименьшее общее кратное знаменателей чисел
- наименьшее общее кратное знаменателей чисел 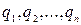 .
.
