Цель работы: на основании свойств реального газа определить с помощью аспирационного психрометра влажность воздуха

Лабораторная работа № 2. 5.

Изучение свойств реального газа. Влажность

Цель работы: на основании свойств реального газа определить с помощью аспирационного психрометра влажность воздуха.

I. Основные понятия и определения

Существенными отличиями реального газа от идеального, молекулы которого не имеют размеров и не взаимодействуют, является конечный размер молекул и взаимодействие электромагнитной природы между ними. Уравнением состояния реального газа является уравнение Ван – дер – Ваальса, которое получается из уравнения Менделеева – Клайперона введением поправок на конечный объём молекул b, взаимное притяжение а/V² и для моля газа, имеет вид:

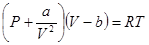. (1)

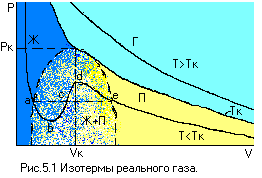Уравнение (1) кубическое относительно объёма и поэтому при T = const одному значению Р может соответствовать три значения V. Приведённые на рис. 5.1 изотермы реального газа имеют сложную форму и поэтому в зависимости от температуры, давления и объёма реальный газ может находиться в состоянии газа «Г», пара «П», жидкости «Ж». Поэтому под паром понимается такое газообразное состояние вещества, из которого изотермическим сжатием оно может быть переведено в жидкое состояние. При этом температура вещества должна быть ниже критической Т_к. Если же Т > Т_к, то изотермическим сжатием вещество не может быть переведено в жидкое состояние и вещество находится в состоянии газа.

Пунктирные участки изотерм, а – в, d – e,соответствующие перегретой жидкости и переохлаждённому пару в обычных условиях не осуществляются. Падающие пунктирные участки b – c – d изотерм соответствуют абсолютно неустойчивому состоянию.

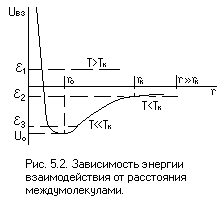Объяснение поведения реального газа достаточно наглядно иллюстрируется кривой зависимости энергии взаимодействия молекул от расстояния между ними, которая имеет вид потенциальной ямы глубиной U₀. Очевидно, что если средняя энергия молекул 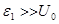, то движение молекул неограниченно в сторону увеличения расстояния между ними — состояние газа. Если же энергия молекул сравнима с глубиной потенциальной ямы 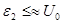, то движение временно ограничено размерами ямы — жидкое состояние. Если же 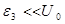, то молекулы не могут покинуть пределы потенциальной ямы и колеблются около положения равновесия – твёрдое состояние.

Рассмотрим жидкое состояние. Из рис.5.2 следует, что если расстояние между молекулами r>>r_k, то и при условии 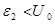молекулы очень слабо взаимодействуют друг с другом – вещество находится в состоянии пара. Чтобы пар перевести в жидкое состояние, его необходимо сжать до объёма соответствующего расстоянию между молекулами r ≈ r_k.

Как следует из рис.5.1 при определённых значениях объёма и давления (область P–V, ограниченная пунктирной кривой) газ и жидкость существуют одновременно, образуя смесь, компоненты которой имеют одинаковые давления и температуру. Следовательно, пар и жидкость находятся в термодинамическом равновесии, и пар называется насыщенным. Другими словами, под насыщенным паром понимается пар, переходящий в жидкость без изменения температуры и давления. Давление, при котором происходит сжижение пара, называется упругостью насыщенного пара, а температура — точкой росы, т.к. пар конденсируется в капельки. Пар, обладающий меньшей упругостью, чем насыщенный при той же температуре (правая ветвь изотермы), называется ненасыщенным.

В технических приложениях относительно водяного пара вместо понятия упругости используются понятия абсолютной влажности р_а, под которой понимается парциальное давление водяных паров в атмосфере (часть атмосферного давления) или масса водяных паров в единице объёма воздуха. Соответственно р_а, измеряется в Па или кг/м³. Однако, как следует и рис. 5.1, давление пара зависит от температуры, и поэтому одно и то же давление пара может соответствовать или не соответствовать насыщенному состоянию в зависимости от температуры. Упругость насыщенного пара растёт с ростом температуры и поэтому для определения близости состояния пара к насыщению при данной температуре вводится понятие относительной влажности r = p_a/p_н, где p_н — упругость насыщенного пара при той же температуре при которой, определено давление (абсолютная влажность) насыщенного пара p_a.

Рассмотрим кратко процессы испарения и охлаждения жидкости. При испарении жидкости наиболее быстрые молекулы покидают жидкость, унося с собой энергию. Поэтому температура жидкости, в которой остаются менее энергичные молекулы, понижается. Для поддержания температуры жидкости неизменной к ней необходимо подводить тепло. Количество тепла, которое необходимо сообщить единице массы жидкости, чтобы перевести её в пар при неизменной температуре, называется скрытой теплотой испарения. При сжижении пара, вследствие притяжения молекул, их скорости возрастают, и температура жидкости увеличивается. При этом выделяется теплота, равная скрытой теплоте испарения.

Для обозначения термодинамического состояния вещества вводится понятие фазы. Под фазами понимаются состояния вещества, разделённые фазовыми переходами. Фазовый переход — это скачкообразный переход вещества из одного состояния в другое. Под скачкообразностью понимается мгновенное изменение характерного параметра состояния (фазы) после перехода всего вещества из одного состояния в другое. С примере с охлаждением пара или испарения жидкости, температура не меняется пока весь пар не перейдёт в жидкость или вся жидкость не испариться. Следовательно, переход пар – жидкость и наоборот является фазовым переходом. Если при фазовом переходе поглощается или выделяется тепло – переход первого рода, в противном случае — второго рода.

В атмосфере Земли вследствие всевозможных испарений содержится огромное количество водяных паров, наличие которых характеризуется понятием «влажность». Влажность воздуха необходимо учитывать для нормальной жизни человека, для хранения продуктов и материалов, в сельском хозяйстве, транспорте, для ряда производственных процессов. Чтобы узнать содержание водяного пара в воздухе, в принципе можно пропустить определённый объём воздуха сквозь поглощающее вещество и определить насколько при этом изменится масса вещества. Оказалось, что численное значение абсолютной влажности мало отличается от парциального давления водяного пара, измеренного в миллиметрах ртутного столба, а его измерить очень просто. Для вычисления влажности пользуются таблицей значений давления насыщенного пара в зависимости от температуры. Абсолютная влажность соответствует точке росы, а максимальное давление пара — температуре окружающей среды. Р_а↔tº_рос; P_max↔tº_ок.

Таблица № 5.1

tº, С	ρн, г/м3	рн, мм.рт.с.	tº, С	ρн, г/м3	рн, мм.рт.с.	tº, С	ρн, г/м3	рн, мм.рт.с.	tº, С	ρн, г/м3	рн, мм.рт.с.
	4,8	4,6		8,3	8,0		13,6	13,6		21,8	22,4
	5,2	4,9		8,8	8,6		14,5	14,5		23,0	23,8
	5,6	5,3		9,4	9,2		15,4	15,5		24,4	25,2
	6,0	5,7		10,0	9,8		16,3	16,5		25,8	26,7
	6,4	6,1		10,7	10,5		17,3	17,5		27,2	28,4
	6,8	6,6		11,4	11,2		18,3	18,7		28,7	30,0
	7,3	7,0		12,1	12,0		19,4	19,8		30,3	31,8
	7,8	7,5		12,8	12,8		20,6	21,1		32,0	33,5

II. Методика эксперимента

Для определения влажности воздуха широко используется психрометры. В данной работе используется модель аспирационного психрометра, содержащийся два термометра в трубках, через который механическим вентилятором прокачивается воздух. Резервуар одного из термометров обёрнут влажной материей и поэтому, за счёт испарения его температура ниже температуры окружающей среды. Очевидно, что скорость испарения (величина степени охлаждения «мокрого» термометра) зависит от влажности окружающего воздуха. Количественно охлаждение «мокрого» термометра можно определить из разности притока за счёт теплопроводности тепла из окружающей среды Q₁=aS(T_c-T_м) и оттока его за счёт испарения Q₂= в(Р_н-Р_а)S/Р_а. Здесь: Т_с, Т_м - температуры «сухого» и «мокрого» термометров, S – поверхность испарения, Ра – атмосферное давление, а и в – постоянные и их отношение, А = (а/в) = 8*10^-4 — постоянная психрометра. При установлении термодинамического равновесия температура «мокрого» термометра не меняется, что означает равенство Q₁=Q₂. Тогда для относительной влажности получаем выражение вида:

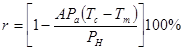. (2)

Используя таблицу 5.1 зависимости упругости насыщенного пара от температуры, можно определить и абсолютную влажность.

Таблица № 5.2

tº, °C
PH, Па*103	1,610	1,708	1,821	1,942	2,032	2,202	2,342	1,490	2,650	2,816

III. Проведение эксперимента и обработка результатов

1. Смочить ткань «мокрого» термометра пипеткой.

2. Включить вентилятор психрометра и выждать 4-5 минут, пока температура «мокрого» термометра не станет постоянной.

3. Определить показания «сухого» и «мокрого» термометров и занести в таблицу № 5.2

4. Определить атмосферное давление по барометру лаборатории и занести в таблицу № 5.2.

r =________%, P_A=_______Па, Ра = ________Па

Таблица № 5.3

№п/п	tºс, °C	tºм, °C	r, %	rср, %	δrср, %	ηr, %

760мм.рт.ст.=1,013*10⁵Па

5. Вычислить относительную влажность по формуле 5.2 и занести в таблицу.

6. Выждав, когда температуры «сухого» и «мокрого» термометров сравняются, повторить измерения по пунктам 2-5.

7. Определить абсолютную влажность воздуха с помощью таблицы 5.1 по формуле .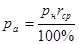

8. Сравнить результаты измерения по показаниям лабораторного гигрометра.