Розв`язання показникових рівнянь зведенням до однієї основи
Схема розв`язання:
1. Перетворити ліву та праву частини рівняння до вигляду степеня з однією основною але з різними показниками.
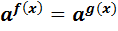
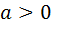 ,
, 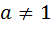
2. Якщо рівні основи степеня , тоді рівні їх показники, тобто 
Приклади. Розв`язати рівняння:
1) 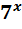 = 49 ; 2)
= 49 ; 2) 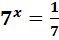 ; 3)
; 3) 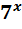 =
= 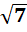 4)
4) 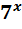 = 1
= 1
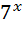 =72
=72 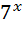 =7-1
=7-1 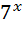 =
= 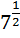
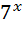 =70
=70
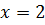
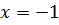
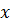 =
= 
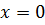
Відповідь : 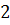 Відповідь:
Відповідь: 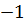 Відповідь:
Відповідь:  Відповідь:
Відповідь: 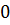
5) 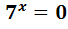 6)
6) 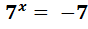
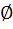
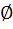
Оскільки 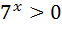 завжди Оскільки
завжди Оскільки 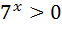 завжди
завжди
Відповідь : коренів не має Відповідь : коренів не має
7) 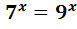
Поділимо обидві частини рівняння на вираз 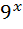 (
( 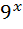 > 0).
> 0).
Отримаємо: 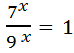
Зверніть увагу! 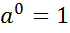 |
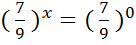 ;
; 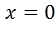
Відповідь: 0
Зверніть увагу! 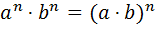 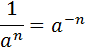 |
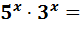
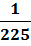
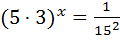
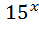
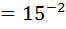
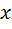
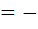 2
2
Відповідь: 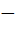 2.
2.
Зверніть увагу! 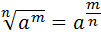 |
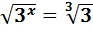
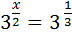
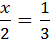
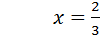
Відповідь: 
Зверніть увагу! 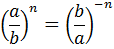 |
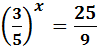
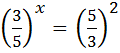
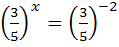
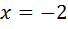
Відповідь: 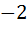
Зверніть увагу! 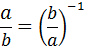 |
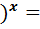

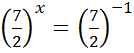
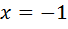
Відповідь: 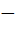 1
1
12) (0,5 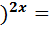 16 ; 13) (
16 ; 13) ( 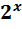 -1
-1 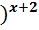
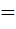 1 ;
1 ;
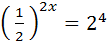 ;
; 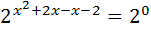 ;
;
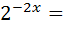 24 ;
24 ; 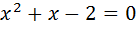 ;
;
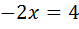 ;
; 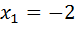 ;
;
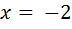 .
. 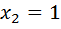 .
.
Відповідь 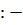 2 Відповідь:
2 Відповідь: 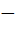 2; 1.
2; 1.
Зверніть увагу! 0,125 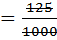 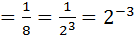 |
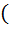 0,125
0,125 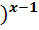
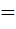 4;
4; 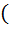 2-3
2-3 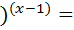 22 ;
22 ;
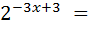 22
22
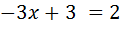 ;
;
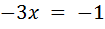 ;
;
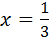
Відповідь: 
2) Розв`язання показникових рівнянь за допомогою розкладанняоднієї з частин на множники (винесення степеня з найменшим показником, коефіцієнти показників цих степенів набувають однакових значень).
Схема розв`язання:
1) Звести всі степені до однієї основи.
2) Винести за дужки степінь із найменшим показником.
У такому випадку в дужках завжди утворюється числовий вираз
без змінної 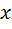 .
.
3) Перетворити рівняння до найпростішого показникового рівняння
та розв`язати його.
Приклади.
Розв`язати рівняння:
1) 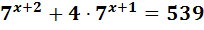
За дужки винесемо степінь з найменшим показником 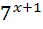
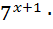 (7+4)
(7+4) 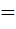 539; 1)
539; 1) 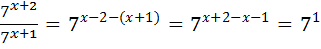
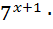 11
11 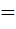 539 ; 2)
539 ; 2) 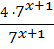
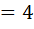
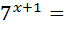 739:11
739:11
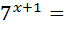 49;
49;
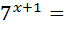 72;
72;
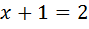 ;
;
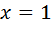
Відповідь: 1.
2) 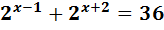
За дужки винесемо степінь з найменшим показником.
1) 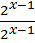 =1 2) =1 2) 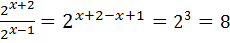 |
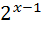
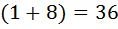 ;
; 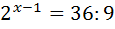 ;
;
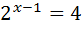 ;
;
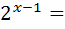 22
22
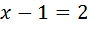 ;
;
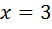
Відповідь: 3
3) 704
За дужки винесемо степінь з найменшим показником.
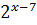 (23+22
(23+22 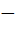 1)
1) 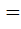 704; 1)
704; 1) 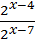 =2х-4-(х-7)
=2х-4-(х-7) 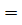 2х-4-х+7
2х-4-х+7 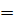 23
23
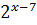 (8+4
(8+4 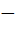 1)
1) 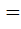 704 ; 2)
704 ; 2) 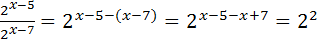
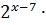 11
11 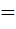 704 ; 3)
704 ; 3) 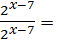 1
1
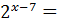 704:11 ;
704:11 ;
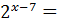 64 ;
64 ;
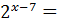 26 ;
26 ;
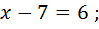
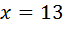
Відповідь: 13
3) Розв`язання показнкових рівнянь, що зводяться до квадратних рівнянь
Схема розв`язання:
1. Позбавитися числових доданків у показниках степенів.
2. Звести всі степені до однієї основи.
3. Зробити заміну змінної.
4. Розв`язати отримане рівняння.
5. Повертаючись до заміни , розв`язати найпростіше показникове
рівняння.
Приклади
Розв`язати рівняння:
1) 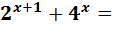 80. Зводимо степені до основи
80. Зводимо степені до основи 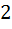
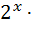 21+
21+ 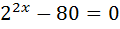 ;
; 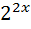 +2
+2 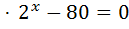
Зробимо заміну змінної: 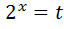 ,
, 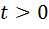
Маємо:
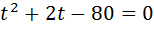
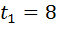
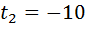 – не задовольняє умову
– не задовольняє умову 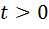
Повертаючись до заміни, маємо:
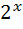 = 8
= 8
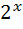 =23
=23
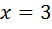 Відповідь: 3.
Відповідь: 3.
Зверніть увагу! 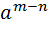 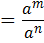 |
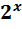 +
+ 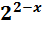
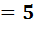 ;
; 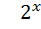 +
+ 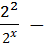 5
5 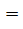 0
0
Зробимо заміну змінної : 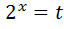 ,
, 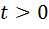 .
.
Маємо:
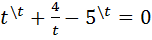 ;
;
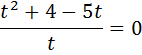
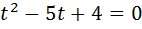
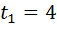
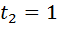
Повертаючись до заміни, маємо:
1) 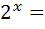 4 ; 2)
4 ; 2) 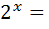 1
1
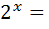 22
22 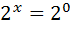
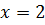
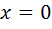
Відповідь: 2; 0.
ОДЗ: 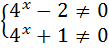 |
3) 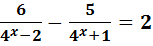
Зробимо заміну змінної : 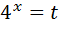 ,
, 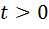
Маємо:
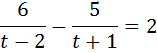
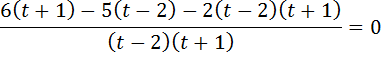
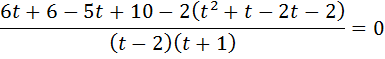
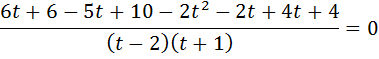
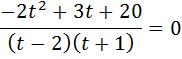
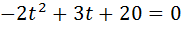
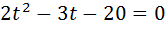
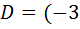 )2
)2 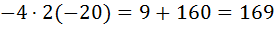
t1= 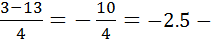 не задовольняє умову
не задовольняє умову 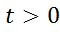
t2 = 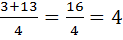
Повертаючись до заміни, маємо:
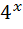 =4
=4
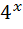 =41
=41
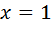
Відповідь: 1.
4) Розв`язання однорідних показникових рівнянь
Рівняння виду
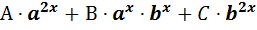 =0, деА,В,С- числа називається однорідним показниковим рівнянням.
=0, деА,В,С- числа називається однорідним показниковим рівнянням.
