Доказательство (условия совместности системы)
Свойства определителей
· При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.
· Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.
· Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.
· Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).
· Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
· Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.
· Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.
· Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
· Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей (cм. также формулу Бине-Коши).
· С использованием индексной нотации определитель матрицы 3×3 может быть определён с помощью символа Леви-Чивита из соотношения:

4.Определитель треугольной матрицы равен произведению элементов на её главной диагонали
5. Теорема о разложении определителя по элементам строки. Определитель матрицы A равен сумме произведений элементов строки на их алгебраические дополнения:
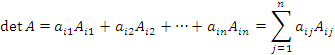 .
.
Теорема о разложении определителя по элементам столбца. Определитель матрицы A равен сумме произведений элементов столбца на их алгебраические дополнения:
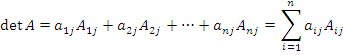 .
.
6. теорема аннулирования. Сумма, произведений элементов одного из столбцов (строк) матрицы на соответствующие алгебраические дополнения элементов другого столбца (строки) равна нулю.
Доказательство.
Докажем к примеру, что сумма произведений элементов второго столбца на соответствующие алгебраические дополнения элементов первого столбца равна нулю. Пусть задан определитель (1.5). Тогда имеем разложение (1.6)
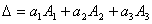 .
.
Алгебраические дополнения 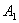 ,
,  ,
, 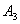 не зависят от самих элементов
не зависят от самих элементов 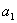 ,
, 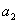 ,
, 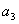 . Поэтому если в обеих частях равенства (1.6) числа
. Поэтому если в обеих частях равенства (1.6) числа 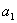 ,
, 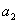 ,
, 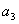 заменить произвольными числами
заменить произвольными числами 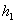 ,
, 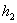 ,
, 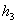 , то получится верное равенство
, то получится верное равенство
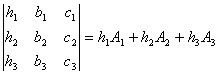 (1.10).
(1.10).
Если теперь в равенстве (1.10) в качестве 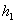 ,
, 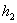 ,
, 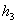 взять элементы
взять элементы 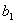 ,
, 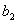 ,
,  второго столбца, то согласно свойству (3) определитель с двумя одинаковыми столбцами равен нулю.
второго столбца, то согласно свойству (3) определитель с двумя одинаковыми столбцами равен нулю.
7. Правило треугольников: определитель равен алгебраической сумме произведений элементов, расположенных на главной и побочной диагоналях и в вершинах реугольников с основаниями параллельными диагоналям. Произведения элементов, расположенных на побочной диагонали и в вершинах треугольников с основаниями параллельными ей, берутся со знаком минус.
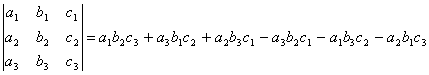
8. Для системы 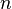 линейных уравнений с
линейных уравнений с 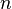 неизвестными (над произвольным полем)
неизвестными (над произвольным полем)
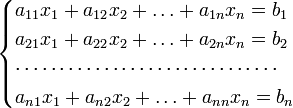
с определителем матрицы системы 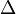 , отличным от нуля, решение записывается в виде
, отличным от нуля, решение записывается в виде

(i-ый столбец матрицы системы заменяется столбцом свободных членов).
9. Сложение и вычитание матриц - одно из простейших действий над ними, т.к. необходимо сложить или отнять соответствующие элементы двух матриц. Главное помнить, что складывать и вычитать можно только матрицыодинаковых размеров, т.е. тех, у которых одинаковое количество строк и одинаковое количество столбцов.
Сумма двух матриц:
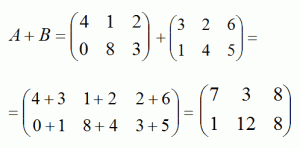
Разность двух матриц:
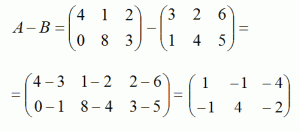
10. Определение. Произведением скаляра 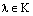 на матрицу
на матрицу 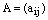 называется матрица
называется матрица 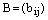 тех же размеров, что и матрица А, где элементы
тех же размеров, что и матрица А, где элементы 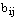 определяются равенством
определяются равенством 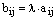 , для всех значений индексов.
, для всех значений индексов.
11. Другими словами, чтобы умножить две матрицы, нужно каждую строку первой матрицы умножить на каждый столбец второй матрицы. Умножая первую строку первой матрицы на каждый столбец второй матрицы мы получим все элементы первой строки матрицы произведения, затем делаем то же самое для второй строки первой матрицы и т.д.
Замечание. Из определения следует, что умножение матриц возможно только тогда, когда ширина первой матрицы (т.е. число ее столбцов) равна высоте второй (т.е. числу ее строк)
Пример.
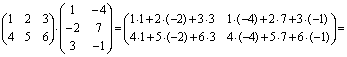
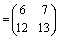 .
.
12.
| Возведением квадратной матрицы A в степень n, где n - натуральное число, называется произведение матрицы A саму на себя n раз. Причем, | |
| A 0 = E, | |
где E - единичная матрица. Определитель произведения квадратных матриц равен произведению определителей сомножителей, то есть 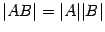 . 13. Транспонированная матрица — матрица . 13. Транспонированная матрица — матрица 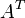 , полученная из исходной матрицы , полученная из исходной матрицы 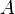 заменой строк на столбцы. Формально, транспонированная матрица для матрицы заменой строк на столбцы. Формально, транспонированная матрица для матрицы 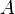 размеров размеров 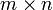 — матрица — матрица 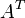 размеров размеров 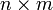 , определённая как AT[i, j] = A[j, i]. Например, , определённая как AT[i, j] = A[j, i]. Например, 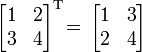 и и 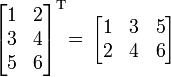 Свойства транспонированных матриц · Свойства транспонированных матриц · 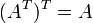 Дважды транспонированная матрица А равна исходной матрице А. · Дважды транспонированная матрица А равна исходной матрице А. · 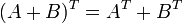 Транспонированная сумма матриц равна сумме транспонированных матриц. · Транспонированная сумма матриц равна сумме транспонированных матриц. · 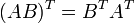 Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке. · Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке. · 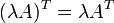 При транспонировании можно выносить скаляр. · При транспонировании можно выносить скаляр. · 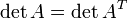 Определитель транспонированной матрицы равен определителю исходной матрицы. 14. Обра́тная ма́трица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E: Определитель транспонированной матрицы равен определителю исходной матрицы. 14. Обра́тная ма́трица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E: 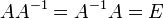 Способы нахождения обратной матрицы Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов: [править]Точные (прямые) методы [править]Метод Гаусса—Жордана Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A−1. При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц Способы нахождения обратной матрицы Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов: [править]Точные (прямые) методы [править]Метод Гаусса—Жордана Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A−1. При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц 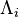 (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции): (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции): 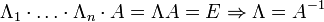 . . 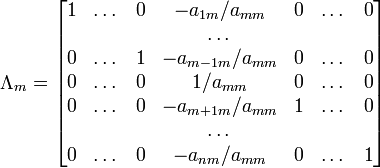 . Вторая матрица после применения всех операций станет равна . Вторая матрица после применения всех операций станет равна 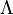 , то есть будет искомой. Сложность алгоритма — , то есть будет искомой. Сложность алгоритма — 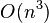 . [править]С помощью матрицы алгебраических дополнений . [править]С помощью матрицы алгебраических дополнений 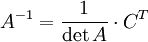 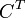 — транспонированная матрица алгебраических дополнений; Полученная матрица A−1 и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя Odet и равна O(n²)·Odet. Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы. 15. Свойства обратной матрицы · — транспонированная матрица алгебраических дополнений; Полученная матрица A−1 и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя Odet и равна O(n²)·Odet. Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы. 15. Свойства обратной матрицы · 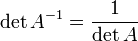 , где , где 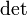 обозначает определитель. · обозначает определитель. · 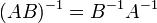 для любых двух обратимых матриц для любых двух обратимых матриц 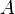 и и 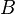 . · . · 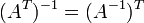 где где 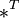 обозначает транспонированную матрицу. · обозначает транспонированную матрицу. · 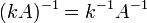 для любого коэффициента для любого коэффициента 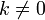 . · Если необходимо решить систему линейных уравнений . · Если необходимо решить систему линейных уравнений 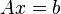 , (b — ненулевой вектор) где , (b — ненулевой вектор) где 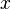 — искомый вектор, и если — искомый вектор, и если 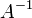 существует, то существует, то 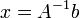 . В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе. 16. Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем. Пусть дана система линейных уравнений с . В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе. 16. Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем. Пусть дана система линейных уравнений с 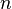 неизвестными (над произвольным полем): неизвестными (над произвольным полем):  Тогда её можно переписать в матричной форме: Тогда её можно переписать в матричной форме: 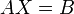 , где , где 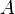 — основная матрица системы, — основная матрица системы, 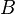 и и 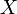 — столбцы свободных членов и решений системы соответственно: — столбцы свободных членов и решений системы соответственно: 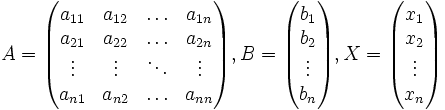 Умножим это матричное уравнение слева на Умножим это матричное уравнение слева на 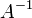 — матрицу, обратную к матрице — матрицу, обратную к матрице 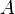 : : 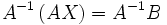 Так как Так как  , получаем , получаем 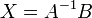 . Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A: . Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A: 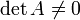 . Для однородной системы линейных уравнений, то есть когда вектор . Для однородной системы линейных уравнений, то есть когда вектор 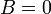 , действительно обратное правило: система , действительно обратное правило: система 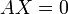 имеет нетривиальное (то есть ненулевое) решение только если имеет нетривиальное (то есть ненулевое) решение только если 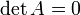 . Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма. 17. Рангом матрицы . Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма. 17. Рангом матрицы 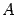 называется наибольший из порядков миноров матрицы называется наибольший из порядков миноров матрицы 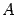 , отличных от нуля. Ранг нулевой матрицы считается равным нулю. Единое, стандартное, обозначение ранга матрицы отсутствует. Итак, первым методом нахождения ранга матрицы является метод перебора миноров. Этот способ основан на определении ранга матрицы.Пусть нам требуется найти ранг матрицы А порядка .Вкратце опишем алгоритм решения этой задачи способом перебора миноров.Если есть хотя бы один элемент матрицы, отличный от нуля, то ранг матрицы как минимум равен единице (так как есть минор первого порядка, не равный нулю).Далее перебираем миноры второго порядка. Если все миноры второго порядка равны нулю, то ранг матрицы равен единице. Если существует хотя бы один ненулевой минор второго порядка, то переходим к перебору миноров третьего порядка, а ранг матрицы как минимум равен двум.Аналогично, если все миноры третьего порядка равны нулю, то ранг матрицы равен двум. Если существует хотя бы один минор третьего порядка, отличный от нуля, то ранг матрицы как минимум равен трем, а мы преступаем к перебору миноров четвертого порядка.И так далее.Отметим, что ранг матрицы не может превышать наименьшего из чисел p и n. Метод Гаусса нахождения ранга матрицы Пусть дана матрица , отличных от нуля. Ранг нулевой матрицы считается равным нулю. Единое, стандартное, обозначение ранга матрицы отсутствует. Итак, первым методом нахождения ранга матрицы является метод перебора миноров. Этот способ основан на определении ранга матрицы.Пусть нам требуется найти ранг матрицы А порядка .Вкратце опишем алгоритм решения этой задачи способом перебора миноров.Если есть хотя бы один элемент матрицы, отличный от нуля, то ранг матрицы как минимум равен единице (так как есть минор первого порядка, не равный нулю).Далее перебираем миноры второго порядка. Если все миноры второго порядка равны нулю, то ранг матрицы равен единице. Если существует хотя бы один ненулевой минор второго порядка, то переходим к перебору миноров третьего порядка, а ранг матрицы как минимум равен двум.Аналогично, если все миноры третьего порядка равны нулю, то ранг матрицы равен двум. Если существует хотя бы один минор третьего порядка, отличный от нуля, то ранг матрицы как минимум равен трем, а мы преступаем к перебору миноров четвертого порядка.И так далее.Отметим, что ранг матрицы не может превышать наименьшего из чисел p и n. Метод Гаусса нахождения ранга матрицы Пусть дана матрица 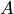 размеров размеров  . Для нахождения ее ранга нужно выполнить следующие действия. 1. Привести матрицу к ступенчатому виду (см. метод Гаусса). 2. В полученной матрице вычислить количество . Для нахождения ее ранга нужно выполнить следующие действия. 1. Привести матрицу к ступенчатому виду (см. метод Гаусса). 2. В полученной матрице вычислить количество  ненулевых строк. Это число равно рангу матрицы ненулевых строк. Это число равно рангу матрицы 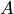 . 18. Определение. Матрицы, полученные в результате элементарного преобразования, называются эквивалентными. Определение Элементарными преобразованиями строк называют: · перестановка местами любых двух строк матрицы; · умножение любой строки матрицы на константу . 18. Определение. Матрицы, полученные в результате элементарного преобразования, называются эквивалентными. Определение Элементарными преобразованиями строк называют: · перестановка местами любых двух строк матрицы; · умножение любой строки матрицы на константу 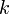 , , 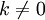 ; · прибавление к любой строке матрицы другой строки. В некоторых курсах линейной алгебры перестановка строк матрицы не выделяется в отдельное элементарное преобразование в силу того, что перестановку местами любых двух строк матрицы можно получить, используя умножение любой строки матрицы на константу ; · прибавление к любой строке матрицы другой строки. В некоторых курсах линейной алгебры перестановка строк матрицы не выделяется в отдельное элементарное преобразование в силу того, что перестановку местами любых двух строк матрицы можно получить, используя умножение любой строки матрицы на константу 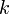 , , 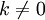 и прибавление к любой строке матрицы другой строки, умноженной на константу и прибавление к любой строке матрицы другой строки, умноженной на константу 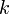 , , 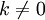 . Аналогично определяются элементарные преобразования столбцов. Элементарные преобразования обратимы. Обозначение . Аналогично определяются элементарные преобразования столбцов. Элементарные преобразования обратимы. Обозначение 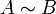 указывает на то, что матрица указывает на то, что матрица 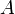 может быть получена из может быть получена из 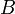 путём элементарных преобразований (или наоборот). 19. Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений: путём элементарных преобразований (или наоборот). 19. Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:
|
Доказательство (условия совместности системы)
[править]Необходимость
Пусть система совместна. Тогда существуют числа 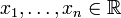 такие, что
такие, что 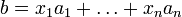 . Следовательно, столбец
. Следовательно, столбец 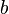 является линейной комбинацией столбцов
является линейной комбинацией столбцов 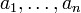 матрицы
матрицы 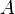 . Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что
. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что 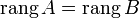 .
.
[править]Достаточность
Пусть 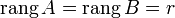 . Возьмем в матрице
. Возьмем в матрице 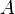 какой-нибудь базисный минор. Так как
какой-нибудь базисный минор. Так как 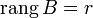 , то он же и будет базисным минором и матрицы
, то он же и будет базисным минором и матрицы 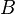 . Тогда согласно теореме о базисном миноре последний столбец матрицы
. Тогда согласно теореме о базисном миноре последний столбец матрицы 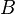 будет линейной комбинацией базисных столбцов, то есть столбцов матрицы
будет линейной комбинацией базисных столбцов, то есть столбцов матрицы 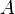 . Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы
. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы 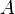 .
.
20.
21.Метод Гаусса: путём элементарных преобразований привести систему к треугольному виду и
выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений.
22.числовым кольцом называется множество чисел, для которых сумма, разность, произведение является элементом того же множества
если в числовом кольце результат деления для Z-ых элементов содержится в том же кольце, то такое кольцо называется числовым полем
1. Свойства: 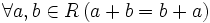 — коммутативность сложения;
— коммутативность сложения;
2. 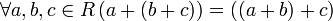 — ассоциативность сложения;
— ассоциативность сложения;
3. 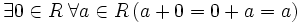 — существование нейтрального элемента относительно сложения;
— существование нейтрального элемента относительно сложения;
4. 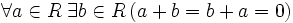 — существование противоположного элемента относительно сложения;
— существование противоположного элемента относительно сложения;
5. 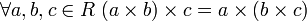 — ассоциативность умножения (некоторые авторы не требуют выполнения этой аксиомы[1])
— ассоциативность умножения (некоторые авторы не требуют выполнения этой аксиомы[1])
6. 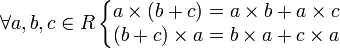 — дистрибутивность.
— дистрибутивность.
23. Ко́мпле́ксные[1] чи́сла (устар. Мнимые числа[2]), — расширение поля вещественных чисел, обычно обозначается 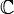 . Любое комплексное число может быть представлено как формальная сумма
. Любое комплексное число может быть представлено как формальная сумма  , где
, где 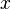 и
и 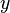 — вещественные числа,
— вещественные числа, 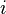 — мнимая единица[3].
— мнимая единица[3].
· Сложение
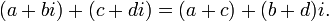
· Умножение
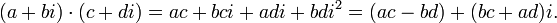
24. Деление
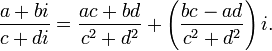
Если комплексное число  , то число
, то число 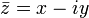 называется сопряжённым (или комплексно сопряжённым) к
называется сопряжённым (или комплексно сопряжённым) к 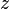 (обозначается также
(обозначается также 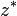 ). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.
). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.
25. Теорема. Пусть 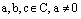 , z – комплексная переменная. Тогда квадратное уравнение
, z – комплексная переменная. Тогда квадратное уравнение 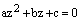 имеет ровно два корня (они могут быть равными), которые можно найти по формуле:
имеет ровно два корня (они могут быть равными), которые можно найти по формуле: 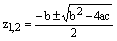 .
.
26. Та запись комплексного числа, которую мы использовали до сих пор, называется алгебраической формой записи комплексного числа. Часто бывает удобна немного другая форма записи комплексного числа. Пусть 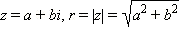 и φ = arg z. Тогда по определению аргумента имеем:
и φ = arg z. Тогда по определению аргумента имеем:
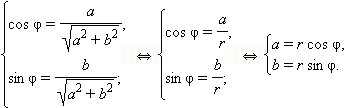 |
Отсюда получается
| z = a + bi = r(cos φ + i sin φ). |
Такая форма называется тригонометрической формой записи комплексного числа. Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.
