Виды несовершенства скважин.

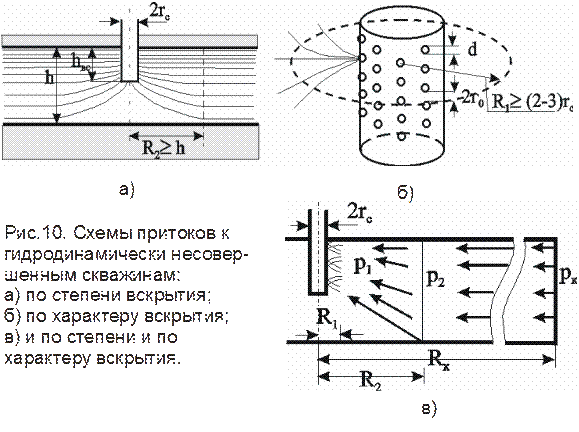
Различают три вида несовершенства скважин, рис. 10:

1) несовершенная скважина по степени вскрытия - это скважина с открытым забоем, вскрывшая пласт не на всю мощность, а только на некоторую глубину b.

2) несовершенная скважина по характеру вскрытия – это скважина, вскрывшая пласт на всю его мощность, но сообщающаяся с пластом только через отверстия в колонне труб (перфорация), в цементном кольце или в специальном фильтре.

3) на практике чаще всего встречаются скважины несовершенные как по степени, так и по характеру вскрытия пласта.

Дебит скважины, гидродинамически несовершенной по степени вскрытия при условии, что радиус контура питания R_к ≥ 0,5 h, можно определить по формуле М.Маскета:

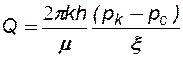(5.1)

где: ,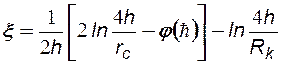

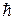=b/h – относительное вскрытие пласта,

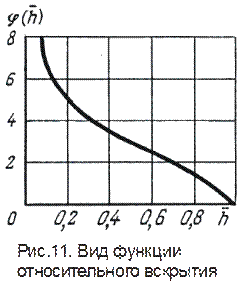
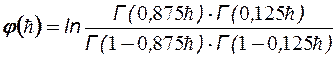- функция относительного вскрытия, представлена графически на рис.11.

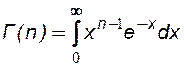- интеграл Эйлера второго рода или гамма-функция, которая табулирована в различных математи-ческих справочниках.

При условии, что величина вскрытия b мала по сравнению с мощностью пласта h (b<<h) и радиус зоны проявления несовершенства скважины по степени вскрытия R₀=1,5h, можно восполь-зоваться формулой И.А. Чарного:

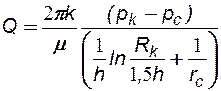(5.2)

Для скважины бесконечной мощности 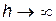дебит можно вычислить по формуле Н.К. Гиринского:

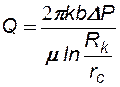(5.3)

Дебит скважины, несовершенной как по степени, так и по характеру вскрытия можно подсчитать по обобщенной формуле Дюпюи с добавочными фильтрационными сопротивлениями:

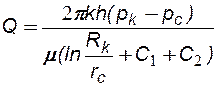(5.4)

где: С₁ - дополнительное фильтрационное сопротивление, обусловленное несовершенством по степени вскрытия, а С₂ - дополнительное фильтрационное сопротивление, обусловленное несовершенством по характеру вскрытия.

С₁ и С₂ можно определить из графиков В.И. Щурова, построенным по данным исследования притока жидкости к скважинам с двойным видом несовершенства на электролитических моделях, рис.12-13.

Величина С₁ представлена на рисунке 12 в зависимости от параметров: 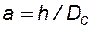и 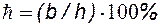, где D_c –диаметр скважины.

Величину С₁ можно оценить по приближенным формулам:

И.А.Чарного: 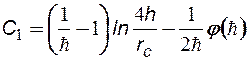(5.5)

А.М. Пирвердяна: (5.6)

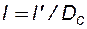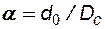Величина С₂ представлена на рисунке 13 в зависимости от параметров: nD_c, и , где 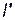- глубина проникновения пуль в породу, d₀ - диаметр отверстий, n - число прострелов на 1 м вскрытой мощности пласта.

Формулу (5.4) можно записать иначе, введя понятие приведенного радиуса скважины:

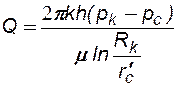(5.7)

где: 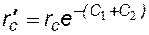- приведенный радиус, такой радиус совершенной скважины, дебит которой равен дебиту реальной несовершенной скважины.

Гидродинамическое несовершенство скважины можно оценить при

помощи коэффициента совершенства скважины d:

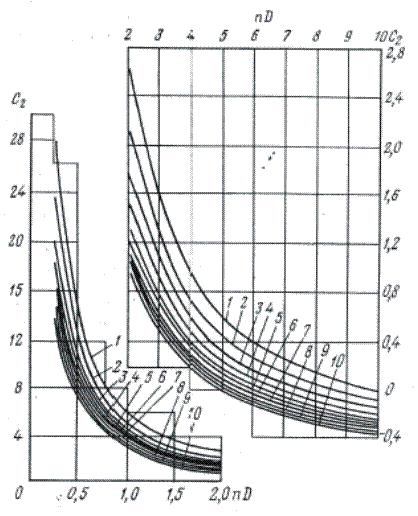
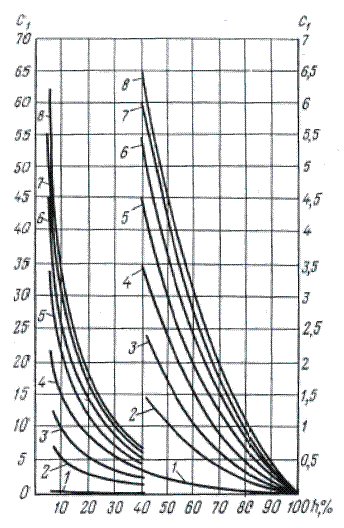
Рис.12. Графики В.И. Щурова для определения С1. Номерам кривых соответствуют значения а: № кривой а

Рис.13. Графики В.И. Щурова для определения С2 при l=0,5. Номерам кривых соответствуют значения a: № кривой a 0,02 0,04 0,06 0,08 0,1 0,12 0,14 0,16 0,18 0,2

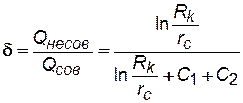(5.8)

Задачи к разделу 5

Задача 5.1

Определить скорость фильтрации у входа в скважину несовершенную по степени вскрытия, если мощность пласта h =25 м, относительное вскрытие пласта 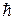=0,6, радиус скважины r_с = 0,1м, дебит скважины Q = 250м³/сут.

Задача 5.2

Гидродинамически несовершенная скважина, вскрывает пласт мощностью 20 м на глубину 10 м. Радиус скважины 10 см, а радиус контура питания – 200м.

Каково превышение фактического дебита, определенного по формуле Маскета, над дебитом в случае строго плоскорадиального потока к скважине с частичным вскрытием пласта?

Задача 5.3

Используя графики Щурова, найти коэффициенты, определяющие дополнительные фильтрационные сопротивления, обусловленные несовершенством по степени и по характеру вскрытия, а также приведенный радиус и коэффициент совершенства скважины, считая, что диаметр скважины равен 24 см. Скважина вскрывает пласт с радиусом контуром питания 500 м, мощностью 9,6 м на величину 5,76 м. Число прострелов на 1 м вскрытой мощности пласта равна 13 отв/м, глубина проникновения пуль в породу 12 см, диаметр отверстий 0,48 см.

Задача 5.4

Скважину исследовали по методу установившихся отборов, изменяя диаметр штуцера и замеряя забойное давление глубинным манометром. Результаты приведены в таблице:

Dр, кгс/см2
Q, 10-6 м3/с

Определить коэффициент проницаемости, если мощность пласта h=32 м, вскрытие пласта b=21,4м, диаметр скважины D_c=20 см, число прострелов на 1 м вскрытой мощности пласта равна n =10 отв/м, глубина проникновения пуль в породу l’ =10 см, диаметр отверстий d₀ =1,2см, радиус контура питания R_k = 300м, динамический коэффициент скважины m = 4сПз.

Задача 5.5

Какому коэффициенту С = С₁ + С₂, определяющему дополнительное фильтрационное сопротивление обусловленное несовершенством скважины, соответствует коэффициент совершенства d = 0,75?

Радиус скважины r_c = 0,1 м, радиус контура питания R_k = 1км.

Определить также приведенный радиус скважины.

Задача 5.6

Определить значение числа Рейнольдса по формулам Щелкачева и Миллионщикова у стенки гидродинамически несовершенной по характеру вскрытия нефтяной скважины, если известно, что эксплуатационная колонна перфорирована. На каждом погонном метре колонны прострелено 10 отверстий диаметром d₀ =10мм, мощность пласта h = 15м, проницаемость пласта k = 1Д, пористость т = 18%, коэффициент вязкости нефти m = 4 сПз, плотность нефти ρ = 870 кг/м³ и дебит скважины составляет 140м³/сут.