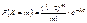Простейший Пуассоновский поток

Моменты n-го порядка. Дисперсия. Среднее квадратическое отклонение.

МО в теории вероятностей относится к типу характеристик положения (см. далее мода, медиана), кроме них используется еще ряд числовых характеристик различного назначения, среди них особое значение имеют моменты (начальные, центральные).Положим g(x)=x^S.

Опр.Начальным моментом S-го порядка СВ Х называется a_S=M[X^S]. Замечание: Иногда используются абсолютные начальные моменты S-го порядка M[çXç^S].

Для СВДТ: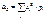

Для СВНТ: .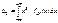

Замечание.

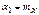– начальный момент 1-го порядка.

Обозначим .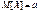

Определение. Центральным моментом S-го порядка называется .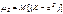

Замечание.

Иногда используются абсолютные центральные моменты S-го порядка.

.

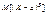Для СВДТ:

.

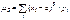Для СВНТ:

.

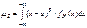Определение. Центральный момент II-го порядка ( 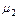) называется дисперсией СВ Х и обозначается .

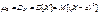Для СВДТ:

.

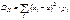Для СВНТ:

.

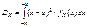Опр. 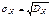– называется средним квадратическим отклонением СВ Х (стандартным отклонением в литературе).

Свойства дисперсии:

1. .

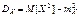Доказательство:

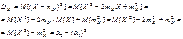g.

2. .

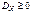Доказательство:

.

(*).

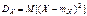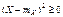По свойству 4 МО и с учетом неравенства (*) получаем доказательство свойства 2 для дисперсии.

3. .

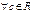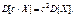
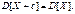
Доказательство:

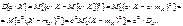
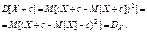Пример.

Пусть на прямой в точках x₁ <x₂ <…<x_k расположены точечные массы p₁,p₂., p_k Σp_i=1:

M[X]=Σx_ip_i (1<i<k) – центр тяжести

D[X]= Σ(x_i-m_i)p_i (1<i<k) – момент инерции масс p_i относительно центра тяжести.

Таким образом, МО характеризует место, вокруг которого группируются массы p_i, а дисперсия – степень разбросанности этих масс относительно МО.

Простейший Пуассоновский поток

На практике часто встречаются ситуации, где имеет место распределение Пуассона. Задача.

Пусть на оси времени 0t случайным образом возникают точки моменты появления каких-то однородных событий. (Например, вызовы на телефонной станции, приход посетителей в магазин и т.д.)). Последовательность таких моментов назовем потоком событий.Предположим, что поток обладает следующими свойствами.

Свойства.

1)Стационарность.Это свойство означает, что вероятность попадания, того или иного числа событий, на участок времени длиной t не зависит от того, где на оси 0t расположен этот участок, а зависит только от его длины t.Из этого следует, что среднее число событий, появляющееся в единицу (l) времени , постоянно.l – интенсивность потока.

2)Ординарность.Это свойство заключается в том, что вероятность попадания на малый участок Dt двух или более событий пренебрежимо мала с вероятностью попадания на него одного события.

Т.е. при Dt®0 вероятность двух или более событий является бесконечно малой более высокого порядка малости, чем вероятность попадания на него одного события.

3)Отсутствие последствия.Это свойство означает, что вероятность попадания некоторого числа событий на заданный участок оси 0t не зависит от того сколько событий попало на любой другой не пересекающийся с ним участок (в частности “будущее” потока не зависит от его “прошлого”).

Опр.Поток событий, обладающий этими 3-мя свойствами называется простейшим (или стационарным) Пуассоновским потоком.

Покажем, как простейший Пуассоновский поток связан с распределением Пуассона.

СВ Х – количество событий, попадающих на участок 0t, длиной t. Покажем, что Х имеет распределение Пуассона. Доказательство:

Разделим участок длины t на n равных частей

Dt =t/n. МО числа событий, попадающих на элементарный участок Dt, равно Dt*l. Согласно свойству 2 (ординарности) можно пренебречь вероятностью попадания на элементарный участок Dt, двух или более событий. Назовем элементарный участок Dt – занятым, если на нем появилось событие из потока. Назовем элементарный участок Dt – свободным, если на нем не появилось событие из потока.A = {участок Dt занят} I_A= 1(участок Dt занят) I_A= 0 (участок Dt свободен). M[I_A]=p_Dt– вероятность того, что участок Dt занят. Среднее число, то есть МО числа событий, попадающих на участок длины Dt, будет равно M[I_A]= Dt*l.

p_Dt= Dt*l. ® p_Dt=l*t/n

Рассмотрим теперь n-участков на временной оси, как n-независимых испытаний (опытов), в каждом из которых (независимость этих испытаний Þ из свойства 3) может появиться событие А и вероятность этого события 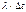. Число занятых элементарных участков – это и есть Х.

СВ Х имеет биномиальное распределение

.

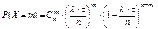
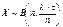Будем теперь неограниченно увеличивать число элементарных участков и найдем при .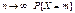

Согласно теореме Пуассона, при 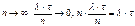,