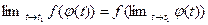Геометрическая интерпретация

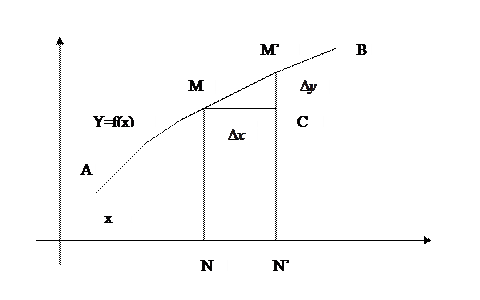
Кривая АВ – график функции f(x).

Рассмотрим точку M(x,y). Даем приращение координате х - 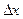. Тогда ордината y получит приращение 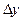. Точка M(x,y) займет положение .

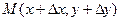Пусть С – точка пересечения прямой параллельной ОХ и перпендикуляра M’N’ на ОХ.

Очевидно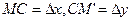

Может случиться, что для некоторого х при стремлении 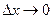точка M’ неограниченно приблизится к М, то есть .

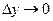В таком случае y=f(x) называется непрерывной при данном значении х.

Определение 2

Функция называется непрерывной в данной точке, если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Используя понятие предела функции, получаем развернутое определение непрерывности функции в точке.

Определение 3

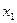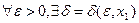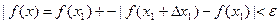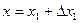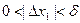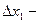Функция f(x) непрерывна в точке тогда и только тогда, когда , такое, что (4), если и , любое допустимое приращение.

Определение 4

Функция f(x) называется непрерывной на данном множестве Х, если

1) она определена на этом множестве, то есть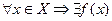

2) непрерывна в каждой точке этого множества, то есть 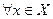справедливо равенство 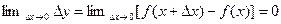(5), где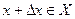

Пример

Исследовать на непрерывность функцию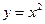

Решение

Давая х приращение 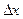, получим .

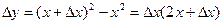Очевидно, каково бы ни было фиксированное значение х, если 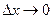, то 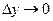, то есть функция непрерывна при любом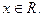

Определение 5

Точка, в которой нарушается непрерывность функции называется точкой разрыва этой функции. Если 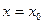- точка разрыва функции y=f(x), то возможны два случая:

1) функция f(x) определена при 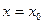, причем 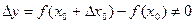при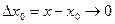

2) функция f(x) не определена при 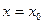и говорить о приращении функции в точке 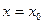не имеет смысла. В этом случае условимся 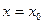называть точкой разрыва функции f(x) только тогда, когда функция f(x) определена в непосредственной близости значения .

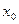Если можно изменить или дополнительно определить функцию f(x) в точке 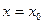, то есть выбрать число 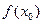, так, что измененная или дополненная функция f(x) будет непрерывна при 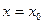, то эта точка называется устранимой точкой разрыва функции f(x).

В противном случае, то есть когда функция f(x) остается разрывной при 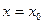при любом выборе числа 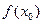значение 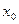называется неустранимой точкой разрыва функции f(x).

Пример 1

Рассмотрим функцию Е(х), равную целой части числа х, то есть, если x=n+q, где n – целое число, 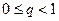, то E(x)=n

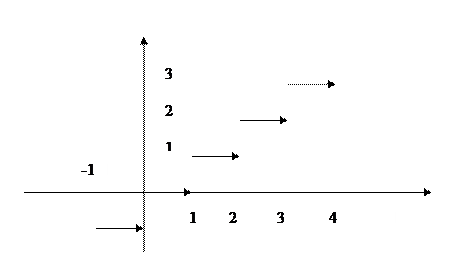
Так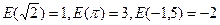

Функция Е(х) разрывная при каждом целочисленном значении аргумента х.

Действительно при x=1 и достаточно малом 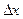получаем

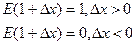
Отсюда, приняв во внимание, что E(1)=1 получим

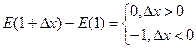
Следовательно, приращение функции 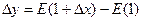не стремится к нулю при 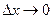, то есть функция разрывная при х=1. Аналогичное рассуждение можно провести и для x=k, где k -целое.

Пример 2

Функция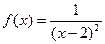не определена при х=2, но имеет смысл для всех значений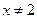

Какое бы значение не приписывали числу f(2), всегда будем иметь 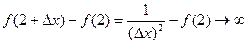при 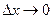. Таким образом, при х=2 при любом выборе значения f(2) при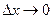 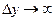, следовательно, эта функция имеет неустранимую точку разрыва при х=2.

В виду важности понятия непрерывности функции приведем другое определение непрерывности функции в точке, эквивалентное, приведенному выше.

Определение 6

Функция f(x) называется непрерывной при 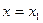, если

1) эта функция определена при ;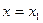

2) имеет место равенство 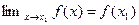(1).

То есть функция непрерывна в данной точке 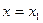, тогда и только тогда, когда предел функции при 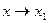равен значению функции в предельной точке. Точка 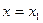- предельная точка области определения функции f(x).

Для функции, непрерывной на множестве Х, в силу формулы (1) для каждого значения 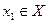выполнено неравенство .

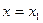Так как 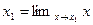, то отсюда получаем 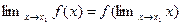(2), то есть , если функция непрерывна, то знаки предела и функции перестановочны.

Справедливо усиленное свойство перестановочности функции f(x) и предела, а именно 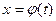- непрерывная функция 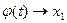при 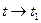, тогда для f(x) имеем