Методика и порядок выполнения работы. 5.1Моделирование произвести на примере прибыли компании за последние четыре года (таблица 4.1).
5.1Моделирование произвести на примере прибыли компании за последние четыре года (таблица 4.1).
Таблица 4.1 – Прибыль компании за последние четыре года
| № квартала, t | Прибыль компании, Уi (№ варианта) | ||||||||||
5.2 В качестве наглядного примера рассмотрим вариант №1.
Пусть имеются поквартальные данные о прибыли компании за последние четыре года (таблица 4.2).
Таблица 4.2 – Прибыль компании, тыс. долл. США
| Квартал Год | I | II | III | IV |
| 72 70 62 52 | 100 92 .80 60 | 90 80 68 50 |
График данного временного ряда (рисунок 4.1) свидетельствует о наличии сезонных колебаний (период колебаний равен 4) и общей убывающей тенденции уровней ряда. Прибыль компании в весенне-летний период выше, чем в осенне-зимний период. Поскольку амплитуда сезонных колебаний уменьшается, можно предположить существование мультипликативной модели. Определим ее компоненты.
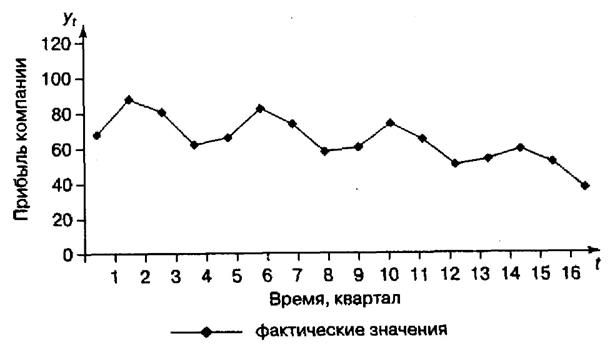
Рисунок 4.1 – Прибыль компании
5.3 Проведем выравнивание исходных уровней ряда методом скользящей средней. Методика, применяемая на этом шаге, полностью совпадает с методикой аддитивной модели. Результаты расчетов оценок сезонной компоненты представлены в таблице 4.3.
5.4 Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 таблицы 4.3). Используем эти оценки для расчета значений сезонной компоненты S (таблица 4.4). Для этого найдем средние за каждый квартал оценки сезонной компоненты St. Взаимопогашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле. В данном случае число периодов одного цикла (год) равно 4 (четыре квартала).
Таблица 4.3 – Расчет оценок сезонной компоненты в мультипликативной модели
| № квартала, t | Прибыль компании, y, | Итого за четыре квартала | Скользящая средняя за четыре квартала | Центрированная скользящая средняя | Оценка сезонной компоненты |
| 2 | |||||
| 81,5 81,0 79,0 76,5 75,0 73,0 70,0 67,0 64,5 62,0 57,0 52,5 48,0 | 81,25 80,00 77,75 75,75 74,00 71,50 68,50 65,75 63,25 59,50 54,75 50,25 | 1,108 0,800 0,900 1,215 1,081 0,811 0,905 1,217 1,075 0,807 0,950 1,194 |
Таблица 4.4 – Расчет сезонной компоненты в мультипликативной модели
| Показатели | Год | № квартала, i | |||
| I | II | III | IV | ||
| – 0,900 0,905 0,950 | – 1,215 1,217 1,194 | 1,108 1,081 1,075 – | 0,800 0,817 0,807 – | ||
| Итого за i-й квартал (за все годы) | 2,755 | 3,626 | 3,264 | 2,424 | |
| Средняя оценка сезонной компоненты для i-го квартала, Si | 0,918 | 1,209 | 1,088 | 0,808 | |
| Скорректированная сезонная компонента, S | 0,913 | 1,202 | 1,082 | 0,803 |
Имеем:
0,918 + 1,209 + 1,088 + 0,808 = 4,023.
Определим корректирующий коэффициент: к = 4/4,023 = 0,9943.
Определим скорректированные значения сезонной компоненты, умножив ее средние оценки на корректирующий коэффициент к.
| Si = Si • k | (4.2) |
где i= 1, 2, …4.
Проверим условие равенства 4 суммы значений сезонной компоненты:
0,913 + 1,202 + 1,082 + 0,803 = 4.
Получим следующие значения сезонной компоненты:
I квартал: S1 = 0,913;
II квартал: S2= 1,202;
III квартал: S3= 1,082;
IV квартал: S4 = 0,803.
Занесем полученные значения в таблицу 4.5 для соответствующих кварталов каждого года (стр. 3).
5.5 Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. Тем самым мы получим величины Т • Е = Y/S (гр. 4 таблица 4.5), которые содержат только тенденцию и случайную компоненту.
Занесем полученные значения в таблицу 4.5 для соответствующих кварталов каждого года (стр. 3).
5.6 Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. Тем самым мы получим величины Т • Е = Y/S (гр. 4 таблицы 4.5), которые содержат только тенденцию и случайную компоненту.
Таблица 4.5 – Расчет выравненных значений Т и ошибок Е в мультипликативной модели
| t | yt | Si | Т•Е = = yt/si | T | T•S | E = = yt/(T•S) | E= =yi - (T•S) | E2 |
| 0,913 | 78,86 | 87,80 | 80,16 | 0,898 | -8,16 | 66,66 | ||
| 1,202 | 83,19 | 85,03 | 102,20 | 0,978 | -2,20 | 4,86 | ||
| 1,082 | 83,18 | 82,25 | 89,00 | 1,011 | 1,00 | 1,00 | ||
| 0,803 | 79,70 | 79,48 | 63,82 | 1,003 | 0,18 | 0,03 | ||
| 0,913 | 76,67 | 76,70 | 70,03 | 1,000 | -0,03 | 0,00 | ||
| 1,202 | 76,54 | 73,93 | 88,86 | 1,035 | 3,14 | 9,85 | ||
| 1,082 | 73,94 | 71,15 | 76,99 | 1,039 | 3,01 | 9,08 | ||
| 0,803 | 72,23 | 68,38 | 54,91 | 1,056 | 3,09 | 9,57 | ||
| 0,913 | 67,91 | 65,60 | 59,90 | 1,035 | 2,10 | 4,43 | ||
| 1,202 | 66,56 | 62,83 | 75,52 | 1,059 | 4,48 | 20,08 | ||
| 1,082 | 62,85 | 60,05 | 64,98 | 1,047 | 3,02 | 9,14 | ||
| 0,803 | 59,78 | 57,28 | 45,99 | 1,044 | 2,01 | 4,03 | ||
| 0,913 | 56,96 | 54,50 | 49,76 | 1,045 | 2,24 | 5,02 | ||
| 1,202 | 49,92 | 51,73 | 62,18 | 0,965 | -2,18 | 4,73 | ||
| 1,082 | 46,21 | 48,95 | 52,97 | 0,944 | -2,97 | 8,79 | ||
| 0,803 | 37,36 | 46,18 | 37,08 | 0,809 | -7,08 | 50,12 |
5.7 Определим компоненту T в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни (Т • Е). Результаты аналитического выравнивания этого ряда представлены ниже:
Константа 90,585150
Коэффициент регрессии -2,773250
Стандартная ошибка коэффициента регрессии 0,225556
R-квадрат 0,915239
Число наблюдений 16
Число степеней свободы 14
Уравнение тренда имеет следующий вид: Т= 90,59-2,773 t.
Подставляя в это уравнение значения t = 1, ..., 16, найдем уровни T для каждого момента времени (гр. 5 таблицы 4.5). График уравнения тренда приведен на рисунке 4.2.
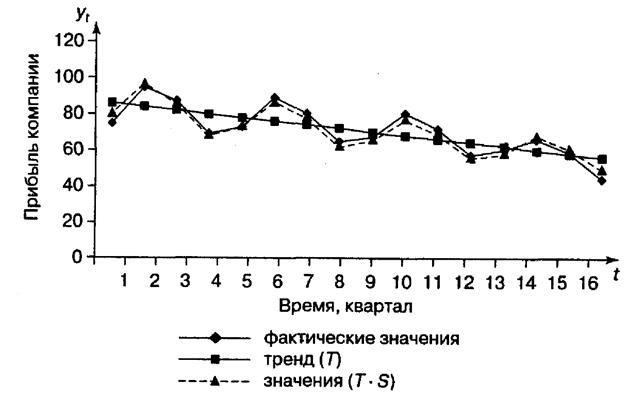
Рисунок 4.2 – Прибыль компании
5.8 Найдем уровни ряда по мультипликативной модели, умножив уровни Т на значения сезонной компоненты для соответствующих кварталов. Графически значения (Т • S) представлены на рисунке 4.2.
5.9 Расчет ошибки в мультипликативной модели производится по формуле:
| E=Y/(T • S). | (4.3) |
Численные значения ошибки приведены в гр. 7 таблицы 4.5. Если временной ряд ошибок не содержит автокорреляции, его можно использовать вместо исходного ряда для изучения его взаимосвязи с другими временными рядами. Для того чтобы сравнить мультипликативную модель и другие модели временного ряда, можно по аналогии с аддитивной моделью использовать сумму квадратов абсолютных ошибок. Абсолютные ошибки в мультипликативной модели определяются как
| E = yt - (T • S). | (4.4) |
В данной модели сумма квадратов абсолютных ошибок составляет 207,40. Общая сумма квадратов отклонений фактических уровней этого ряда от среднего значения равна 5023. Таким образом, доля объясненной дисперсии уровней ряда равна: (1 - 207,40/5023) = 0,959, или 95,9%.
Выявление и устранение сезонного эффекта (в некоторых источниках применяется термин «десезонализация уровней ряда») используются в двух направлениях. Во-первых, воздействие сезонных колебаний следует устранять на этапе предварительной обработки исходных данных при изучении взаимосвязи нескольких временных рядов. Поэтому в российских и международных статистических сборниках часто публикуются данные, в которых устранено влияние сезонной компоненты (если это помесячная или поквартальная статистика), например, показатели объемов производства в отдельных отраслях промышленности, уровня безработицы и т. д. Во-вторых, это анализ структуры одномерных временных рядов с целью прогнозирования уровней ряда в будущие моменты времени.
5.10 Прогнозирование по мультипликативной модели.
Необходимо сделать прогноз ожидаемой прибыли компании за первое полугодие ближайшего следующего года.
Прогнозное значение Ft уровня временного ряда в мультипликативной модели в соответствии с соотношением (4.1) есть произведение трендовой и сезонной компонент. Для определения трендовой компоненты за каждый квартал воспользуемся уравнением тренда Т= 90,59 -2,773•t.
Получим:
T17 = 90,59 -2,773 •17 = 43,401;
T18 = 90,59 - 2,773 •18 = 40,626.
Значения сезонной компоненты равны S1=0,913 (I квартал); S2=1,202 (II квартал).
Таким образом:
F17 = Tl7 • S1 = 43,401 • 0, 913 = 39,626;
F18 = Tl7 • S2 =40,626 • 1, 202 = 48,832.
Прогноз ожидаемой прибыли компании на первое полугодие ближайшего следующего года составит:
(39, 626 + 48,832) = 88,458 тыс. долл. США.
Содержание отчета и его форма
Отчет должен содержать:
6.1 Выровненный исходный ряд методом скользящей средней.
6.2 Расчет значений сезонной компоненты.
6.3 Выравненные данные (Т + Е) модели.
6.4 Расчет значений Т.
6.5 График потребления электроэнергии жителями района (фактические, выровненные и полученные по аддитивной модели значения уровней ряда).
6.6 Расчет ошибок.
6.7 Прогноз ожидаемой прибыли компании за первое полугодие ближайшего следующего года.
6.8 Выводы.
Контрольные вопросы и защита работы
7.1 Сформулируйте общий вид мультипликативной модели временного ряда.
7.2 Как производится расчет абсолютных ошибок?
7.3 Перечислить этапы построения мультипликативной модели.
7.4 С какими целями проводятся выявление и устранение сезонного эффекта?
7.5 Как осуществляется прогноз по данной модели?
Защита работы проводится в устной форме, состоит в предоставлении студентом правильно выполненного отчета по работе, коротком докладе и в ответах на вопросы, представленные выше.
Практическое занятие 29.
Метод экспоненциального сглаживания
Цель и содержание
Цель работы – приобрести навыки прогнозирования при помощи метода экспоненциального сглаживания.
В результате выполнения работы студенты должны:
1. Выбрать аппроксимирующую функцию.
2. Определить параметры уравнения.
3. Определить расчетные значения тренда.
4. Определить параметр сглаживания.
5. Определить окончательную модель прогноза.
Теоретическое обоснование
Метод экспоненциального сглаживания является одним из наиболее эффективных, надежных и широко применяемых методов прогнозирования. Он позволяет получить оценку параметров тренда, характеризующих не средний уровень процесса, а тенденцию, сложившуюся к моменту последнего наблюдения, и при этом отличается простотой вычислительных операций.
Сущность метода заключается в сглаживании исходного динамического ряда взвешенной скользящей средней, веса которой (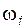 
) подчиняются экспоненциальному закону (рисунок 5.1).
Пусть исходный динамический ряд описывается полиномом вида:
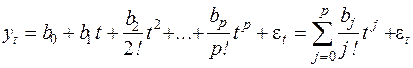 | (5.1) |
где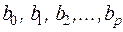 
– коэффициенты;
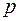– порядок полинома;
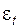– случайная ошибка.
 |
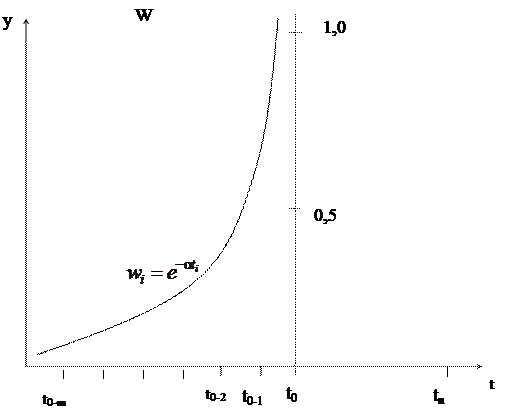Рисунок 5.1 – Коэффициент экспоненциального сглаживания
Метод экспоненциального сглаживания позволяет построить такое описание процесса (5.1), при котором более поздним наблюдениям придаются большие веса по сравнению с ранними наблюдениями, причем веса наблюдений убывают по экспоненте.
Выражение
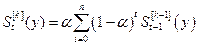 | (5.2) |
называется экспоненциальной средней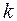 
-гопорядка для ряда 
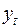, где 
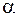– параметр сглаживания.
В расчетах экспоненциальную среднюю определяют, пользуясь рекуррентной формулой, полученной Брауном:
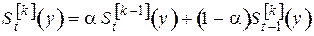 . | (5.3) |
Использование соотношения (5.3) предполагает задание начальных условий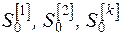 
, которые могут быть определены по формуле Брауна-Мейера:
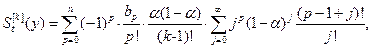 | (5.4) |
где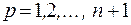 
;
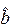– оценки коэффициентов.
Оценки коэффициентов прогнозирующего полинома определяют через экспоненциальные средние по фундаментальной теореме Брауна-Мейера. В этом случае коэффициенты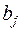 
находят решением системы ( 
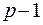) уравнений с ( 
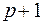) неизвестными, связывающей параметры полинома с исходной информацией.
Рассмотрим применение метода экспоненциального сглаживания для двух наиболее употребительных случаев, когда тренд описывается линейной функцией и параболой.
Линейная модель Брауна
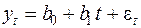 . | (5.5) |
Начальные приближения для случая линейного тренда равны (по формуле (5.4)):
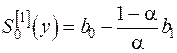 , | (5.6) |
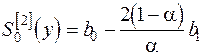 . | (5.7) |
Зная начальные условия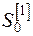 
и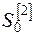 
и значение параметра 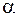, вычисляют экспоненциальные средние 1-го и 2-го порядка:
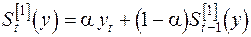 , | (5.8) |
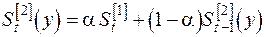 . | (5.9) |
Оценки коэффициентов линейного тренда
| , | (5.10) |
| . | (5.11) |
Прогноз на шагов (на время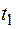 
) равен .
Ошибка прогноза:
| . | (5.12) |
Для метода экспоненциального сглаживания основным и наиболее трудным моментом является выбор параметра сглаживания 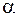, начальных условий и степени прогнозирующего полинома.
Параметр сглаживания 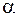определяет оценки коэффициентов модели, а следовательно, результаты прогноза.
В зависимости от величины параметра прогнозные оценки по-разному учитывают влияние исходного ряда наблюдений: чем больше 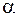, тем больше вклад последних наблюдений в формирование тренда, а влияние начальных условий убывает быстро. При малом 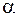прогнозные оценки учитывают все наблюдения, при этом уменьшение влияния более ранней информации происходит медленно.
Для приближенной оценки 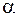известны два основных соотношения:
1) соотношение Брауна, выведенное из условия равенства скользящей и экспоненциальной средней:
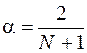 , | (5.13) |
где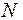 
– число точек ряда, для которых динамика ряда считается однородной и устойчивой (число точек в интервале сглаживания);
Иногда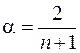 
, где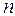 
– число наблюдений (точек) в ретроспективном динамическом ряду;
2) соотношение Мейера:
| , | (5.14) |
где – среднеквадратическая ошибка модели;
– среднеквадратическая ошибка исходного ряда.
Однако достоверно определить и из исходной информации очень сложно, поэтому использование соотношения (5.14) затруднено.
Очевидно, что выбор параметра 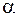нужно связывать с точностью прогноза, поэтому для более обоснованного выбора 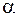можно использовать процедуру обобщенного сглаживания. В этом случае получаются следующие соотношения, связывающие дисперсию прогноза и параметр сглаживания 
:
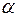для линейной модели
| , | (5.15) |
где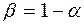 
;
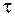– период прогноза;
– среднеквадратическая ошибка аппроксимации исходного динамического ряда.
При 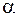=0 выражения, стоящие в правой части формулы (5.15) обращаются в нуль, следовательно, для уменьшения ошибки прогноза необходимо выбирать минимальное .
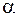В то же время, чем меньше 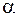, тем ниже точность определения начальных условий, а следовательно, ухудшается и качество прогноза.
Таким образом, использование формулы (5.15) приводит к противоречию при определении параметра сглаживания. В ряде случаев параметр 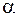выбирают так, чтобы минимизировать ошибку прогноза, рассчитанного по ретроспективной информации.
Качество прогноза во многом зависит от выбора порядка прогнозирующего полинома. Известно, что превышение второго порядка модели не приводит к существенному увеличению точности прогноза, но значительно усложняет расчет.
Аппаратура и материалы
Микрокалькулятор, программное обеспечение MS Excel.