Механические колебания и волны

Основные формулы

Гармонические колебания происходят по закону:

x = A cos(ωt + φ₀),

где x – смещение частицы от положения равновесия, А – амплитуда колебаний, ω – круговая частота, φ₀ – начальная фаза, t – время.

Период колебаний T = .

Скорость колеблющейся частицы:

υ = = – A ω sin (ωt + φ₀),

ускорение a = = – Aω² cos (ωt + φ₀).

Кинетическая энергия частицы, совершающей колебательное движение: E_k = 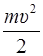= sin²(ωt + φ₀).

Потенциальная энергия:

E_n = cos²(ωt + φ₀).

Периоды колебаний маятников

– пружинного T = ,

где m – масса груза, k – коэффициент жесткости пружины,

– математического T = ,

где l – длина подвеса, g – ускорение свободного падения,

– физического T = ,

где I – момент инерции маятника относительно оси, проходящей через точку подвеса, m – масса маятника, l – расстояние от точки подвеса до центра масс.

Приведенная длина физического маятника находится из условия: l_np = ,

обозначения те же, что для физического маятника.

При сложении двух гармонических колебаний одной частоты и одного направления получается гармоническое колебание той же частоты с амплитудой:

A = A₁² + A₂² + 2A₁A₂ cos(φ₂ – φ₁)

и начальной фазой: φ = arctg .

где А₁, A₂ – амплитуды, φ₁, φ₂ – начальные фазы складываемых колебаний.

Траектория результирующего движения при сложении взаимноперпендикулярных колебаний одной частоты:

+ – cos (φ₂ – φ₁) = sin² (φ₂ – φ₁).

Затухающие колебания происходят по закону:

x = A₀e^{- βt} cos(ωt + φ₀),

где β – коэффициент затухания, смысл остальных параметров тот же, что для гармонических колебаний, А₀ – начальная амплитуда. В момент времени t амплитуда колебаний:

A = A₀e ^{- βt}.

Логарифмическим декрементом затухания называют:

λ = ln = βT,

где Т – период колебания: T = .

Добротностью колебательной системы называют:

D = .

Уравнение плоской бегущей волны имеет вид:

y = y₀ cos ω(t ± ),

где у – смещение колеблющейся величины от положения равновесия, у₀ – амплитуда, ω – круговая частота, t – время, х – координата, вдоль которой распространяется волна, υ – скорость распространения волны.

Знак «+» соответствует волне, распространяющейся против оси X, знак «–» соответствует волне, распространяющейся по оси Х.

Длиной волны называют ее пространственный период:

λ = υT,

где υ–скорость распространения волны, T–период распространяющихся колебаний.

Уравнение волны можно записать:

y = y₀ cos 2π ( + ).

Стоячая волна описывается уравнением:

y = (2y₀ cos ) cos ω t.

В скобки заключена амплитуда стоячей волны. Точки с максимальной амплитудой называются пучностями,

x_п = n ,

точки с нулевой амплитудой – узлами,

x_у = (n + ) .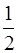

Примеры решения задач

Задача 20

Амплитуда гармонических колебаний равна 50 мм, период 4 с и начальная фаза . а) Записать уравнение этого колебания; б) найти смещения колеблющейся точки от положения равновесия при t=0 и при t = 1,5 с; в) начертить график этого движения.

Решение

Уравнение колебания записывается в виде x = a cos(wt + j₀).

По условию известен период колебаний. Через него можно выразить круговую частоту w = . Остальные параметры известны:

а) x = 0,05 cos( t + ).

б) Смещение x при t = 0.

x₁ = 0,05 cos = 0,05 = 0,0355 м.

При t = 1,5 c

x₂ = 0,05 cos( 1,5 + )= 0,05 cos p= – 0,05 м.

в) график функции x=0,05cos ( t + ) выглядит следующим образом:

Определим положение нескольких точек. Известны х₁(0) и х₂(1,5), а также период колебаний. Значит, через Dt = 4 c значение х повторяется, а через Dt = 2 c меняет знак. Между максимумом и минимумом посередине – 0 .

Задача 21

Точка совершает гармоническое колебание. Период колебаний 2 с, амплитуда 50 мм, начальная фаза равна нулю. Найти скорость точки в момент времени, когда ее смещение от положения равновесия равно 25 мм.

Решение

1 способ. Записываем уравнение колебания точки:

x = 0,05 cos p t,т. к. w = = p.

Находим скорость в момент времени t:

υ = = – 0,05cos p t.

Находим момент времени, когда смещение равно 0,025 м:

0,025 = 0,05 cos p t₁,

отсюда cos pt₁ = 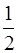, pt₁ = . Подставляем это значение в выражение для скорости:

υ = – 0,05 p sin = – 0,05 p = 0,136 м/c.

2 способ. Полная энергия колебательного движения:

E = ,

где а – амплитуда, w – круговая частота, m –масса частицы.

В каждый момент времени она складывается из потенциальной и кинетической энергии точки

E_k = 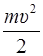, E_п = , но k = mw², значит, E_п = .

Запишем закон сохранения энергии:

= + ,

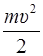отсюда получаем: a²w² = υ ² + w²x²,

υ = w = p = 0,136 м/c.

Задача 22

Амплитуда гармонических колебаний материальной точки А = 2 см, полная энергия Е = 3∙10^-7 Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила F = 2,25∙10^-5 Н?

Решение

Полная энергия точки, совершающей гармонические колебания, равна: E = .(13)

Модуль упругой силы выражается через смещение точек от положения равновесия x следующим образом:

F = k x (14)

В формулу (13) входят масса m и круговая частота w, а в (14) – коэффициент жесткости k. Но круговая частота связана с m и k:

w² = ,

отсюда k = mw² и F = mw²x. Выразив mw² из соотношения (13) получим: mw² = , F = x.

Откуда и получаем выражение для смещения x: x = .

Подстановка числовых значений дает:

x = = 1,5∙10^-2 м = 1,5 см.

Задача 23

Точка участвует в двух колебаниях с одинаковыми периодами и начальными фазами. Амплитуды колебаний А₁ = 3 см и А₂ = 4 см. Найти амплитуду результирующего колебания, если: 1) колебания происходят в одном направлении; 2) колебания взаимно перпендикулярны.

Решение

1) Если колебания происходят в одном направлении, то амплитуда результирующего колебания определится как:

A = ,

где А₁ и А₂ – амплитуды складываемых колебаний, j₁ и j₂–начальные фазы. По условию начальные фазы одинаковы, значит j₂ – j₁ = 0, а cos 0 = 1.

Следовательно:

A = = = А₁+А­₂ = 7 см.

2) Если колебания взаимно перпендикулярны, то уравнение результирующего движения будет:

cos(j ₂ – j ₁) = sin²(j ₂ – j ₁).

Так как по условию j₂ – j₁ = 0, cos 0 = 1, sin 0 = 0, то уравнение запишется в виде: =0,

или =0,

или .

Полученное соотношение между x и у можно изобразить на графике. Из графика видно, что результирующим будет колебание точки на прямой MN. Амплитуда этого колебания определится как: A = = 5 см.

Задача 24

Период затухающих колебаний Т=4 с, логарифмический декремент затухания l = 1,6 , начальная фаза равна нулю. Смещение точки при t = равно 4,5 см. 1) Написать уравнение этого колебания; 2) Построить график этого движения для двух периодов.

Решение

1) Уравнение затухающих колебаний с нулевой начальной фазой имеет вид:

x = A₀e ^-bt cos2p .

Для подстановки числовых значений не хватает величин начальной амплитуды А₀ и коэффициента затухания b.

Коэффициент затухания можно определить из соотношения для логарифмического декремента затухания:

l = bТ.

Таким образом b = = = 0,4 с^-1.

Начальную амплитуду можно определить, подставив второе условие:

4,5 см = A₀ cos 2p = A₀ cos = A₀ .

Отсюда находим:

A₀ = 4,5∙ (см) = 7,75 см.

Окончательно уравнение движения:

x = 0,0775 cos t.

2) Для построения графика сначала рисуем огибающую x = 0,0775 , а затем колебательную часть.

Задача 25

Чему равен логарифмический декремент затухания математического маятника, если за t = 1 мин амплитуда колебаний уменьшилась в два раза? Длина маятника l = 1 м.

Решение

Логарифмический декремент затухания можно найти из соотношения: l= bТ,

где b – коэффициент затухания, Т – период колебаний. Собственная круговая частота математического маятника:

w₀ = = 3,13 с^-1.

Коэффициент затухания колебаний можно определить из условия: 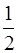A₀ = A₀ e^-bt,

bt = ln2 = 0,693 ,

b = = 0,0116 c^-1.

Поскольку b << w₀, то в формуле w = можно пренебречь b по сравнению с w₀ и период колебаний определить по формуле: T = = 2 c.

Подставляем b и Т в выражение для логарифмического декремента затухания и получаем:

l = bT = 0,0116 с^-1 ∙ 2 с = 0,0232.

Задача 26

Уравнение незатухающих колебаний дано в виде x = 4 sin600 pt см.

Найти смещение от положения равновесия точки, находящейся на расстоянии l = 75 см от источника колебаний, через t = 0,01 с после начала колебаний. Скорость распространения колебаний υ = 300 м/с.

Решение

Запишем уравнение волны, распространяющейся от данного источника: x = 0,04 sin 600 p(t – ).

Находим фазу волны в данный момент времени в данном месте:

t – = 0,01 – = 0,0075 ,

600p ∙ 0,0075 = 4,5p ,

sin 4,5p = sin = 1.

Следовательно, смещение точки x = 0,04 м, т.е. на расстоянии l =75 см от источника в момент времени t = 0,01 c смещение точки максимально.

Список литературы

1. Волькенштейн В.С. Сборник задач по общему курсу физики. – СПб.: СпецЛит, 2001.

2. Савельев И.В. Сборник вопросов и задач по общей физике. – М.: Наука, 1998.