Общая задача интерполирования алгебраическими многочленами. ИМ Эрмита с узлами кратности 2
Общая задача интерполирования ОМ формулир. след. образом. Для ф. 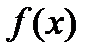 и набора попарно неравных узлов
и набора попарно неравных узлов 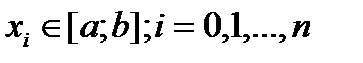 требуется построить ОМ
требуется построить ОМ 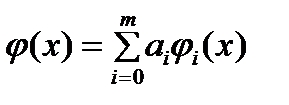 по сист. ф.
по сист. ф. 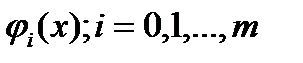 так, чтобы знач. ОМ и его производных до определ. порядка в узлах совпадали с соотв. знач. ф. и ее производных:
так, чтобы знач. ОМ и его производных до определ. порядка в узлах совпадали с соотв. знач. ф. и ее производных:

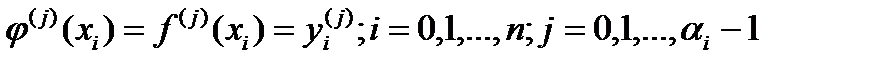 .
.
Ограничимся рассмотр. здесь случая, когда 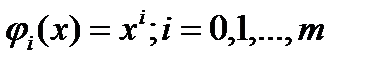 , т.е., общей задачей интерпол. алгебраическими М. Для ф.
, т.е., общей задачей интерпол. алгебраическими М. Для ф. 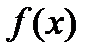 и набора попарно неравных узлов
и набора попарно неравных узлов 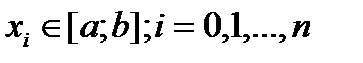 требуется построить М
требуется построить М 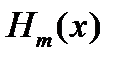 , удовлетв. условиям
, удовлетв. условиям

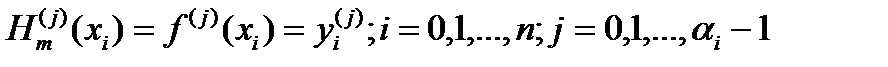 .(1)
.(1)
Рассм. разность 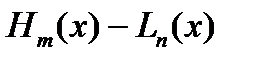 , где
, где 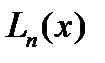 - ИМ Лагранжа для
- ИМ Лагранжа для 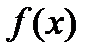 по узлам
по узлам 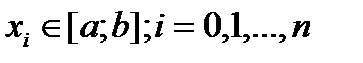 . Т.к.
. Т.к. 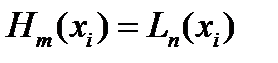 при
при 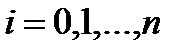 , то
, то 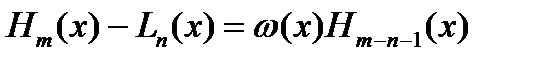 . (2)
. (2)
Исходная задача сведена к построению М 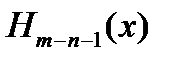 .
.
Продифф. равенство (2): 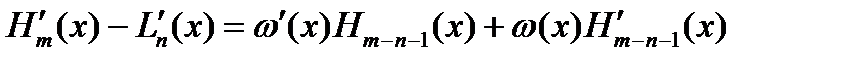 . Для узлов
. Для узлов 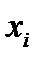 , в кот. заданы знач. произв.
, в кот. заданы знач. произв. 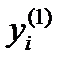 отсюда имеем
отсюда имеем 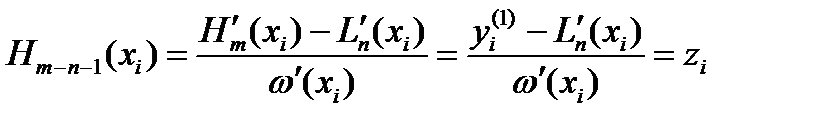 . (3)
. (3)
Дифф. равенство (2) дважды, получим
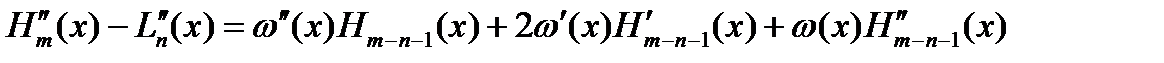 Отсюда для узлов
Отсюда для узлов 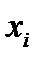 , в кот. заданы знач. произв.
, в кот. заданы знач. произв. 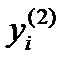 , имеем
, имеем
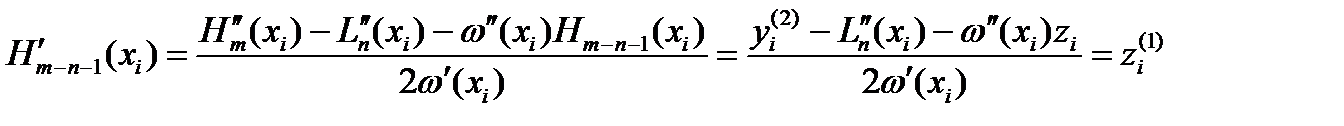 Далее, приходим к задаче постр. М
Далее, приходим к задаче постр. М 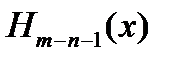 степени
степени 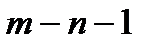 , удовл. усл.
, удовл. усл. 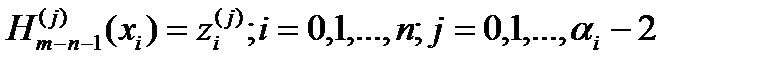 . (4)
. (4)
Для построения М 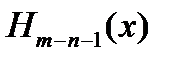 по услов. (4) применяем тот же прием, что и при построении М
по услов. (4) применяем тот же прием, что и при построении М 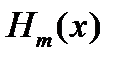 по усл. (1). Повторяя процесс, приходим к задаче построения ИМ по его знач. в узлах, где в (1) задавались знач. старшей производной. Последняя задача решается единственным образом и, следовательно, искомый мн.
по усл. (1). Повторяя процесс, приходим к задаче построения ИМ по его знач. в узлах, где в (1) задавались знач. старшей производной. Последняя задача решается единственным образом и, следовательно, искомый мн. 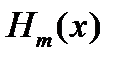 имеет степень
имеет степень 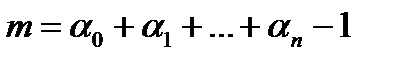 и является единственным.
и является единственным.
Мн. 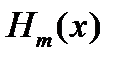 , удовлетв. усл. (1), наз. мн. Эрмитадля ф.
, удовлетв. усл. (1), наз. мн. Эрмитадля ф. 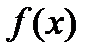 по набору попарно неравных узлов
по набору попарно неравных узлов 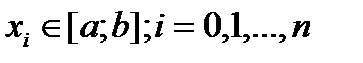 с соотв. кратностями
с соотв. кратностями 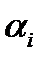 узлов.
узлов.
Проведем построение мн. Эрмита для случая, когда все узлы имеют одинаковую кратность, равную двум. Усл. (1) при этом принимают вид
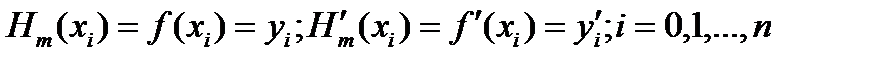 . (5)
. (5)
Используя форм. (2) и (3), получим 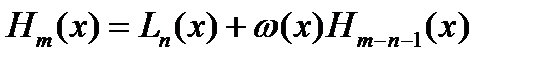 ;
;
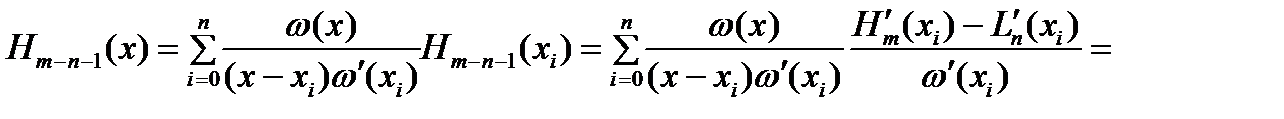
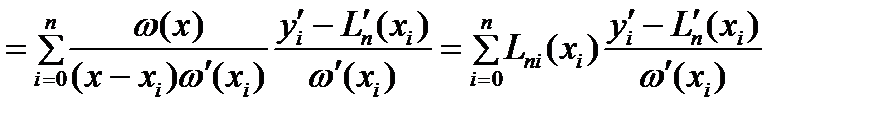 .
.
Т.о., построен искомый ИМ Эрмита
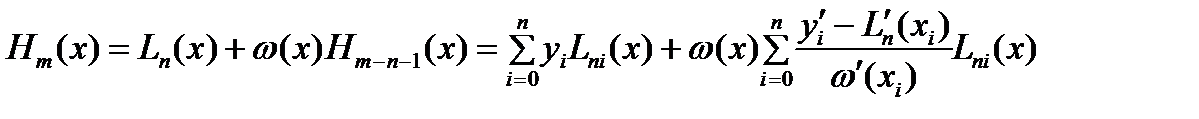 . (6)
. (6)
Проведем в выражении (6) алгебраические преобр. Учтем, что 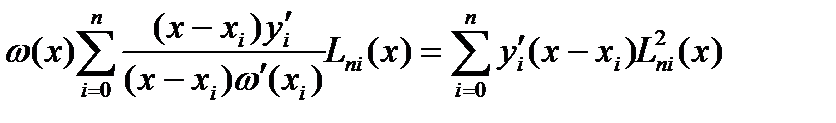 и
и
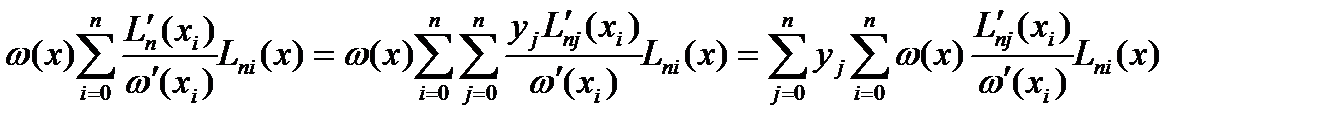 Тогда формула (6) примет вид
Тогда формула (6) примет вид
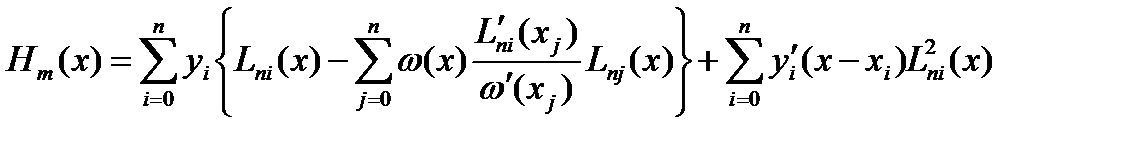 (7)
(7)
Рассм. выражение в фигурных скобках 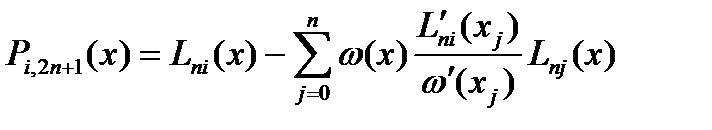 . Это мн. степени
. Это мн. степени 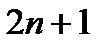 . При этом
. При этом 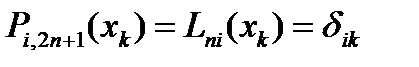
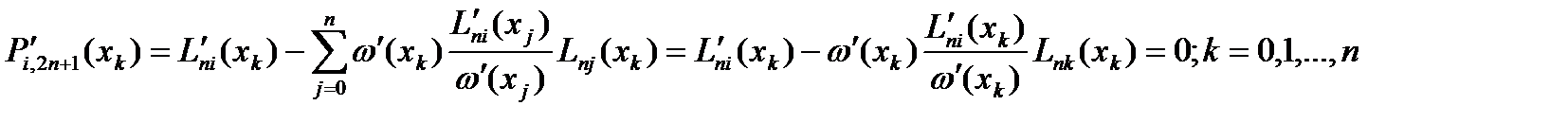 Следов., рассматриваемый мн. представляется в виде
Следов., рассматриваемый мн. представляется в виде 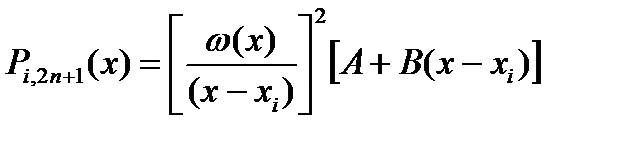 . (8)
. (8)
Полагая в (8) 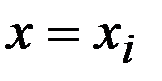 , имеем
, имеем 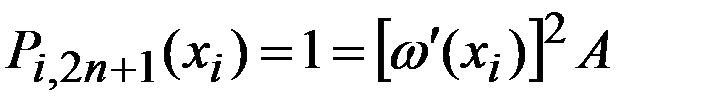 и
и 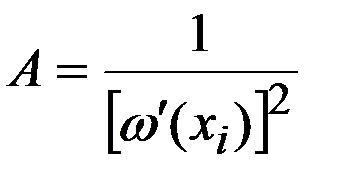 . Из условия
. Из условия
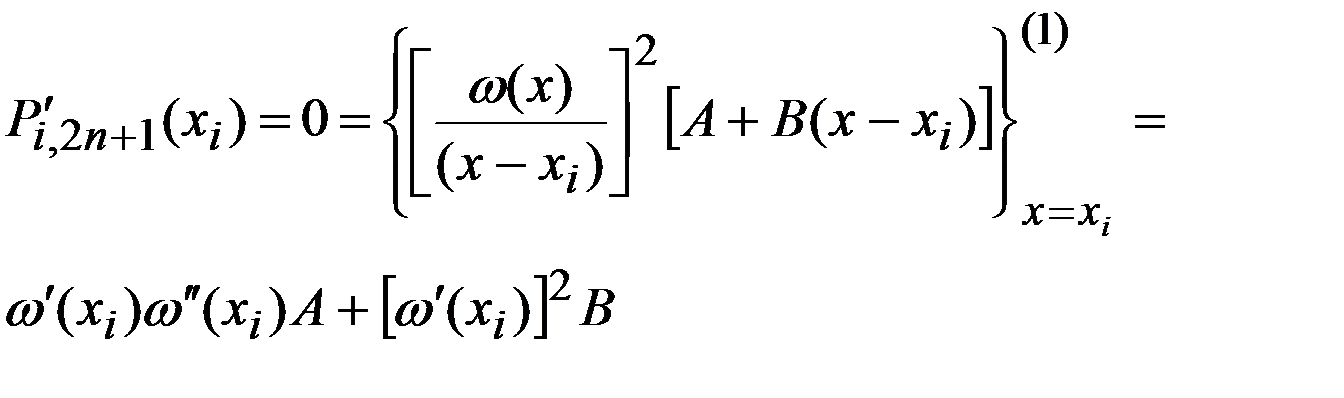 находим
находим
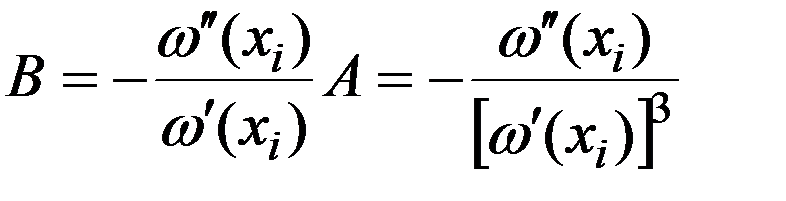 . Подставляя получ. выражения коэффициентов в (8), имеем
. Подставляя получ. выражения коэффициентов в (8), имеем
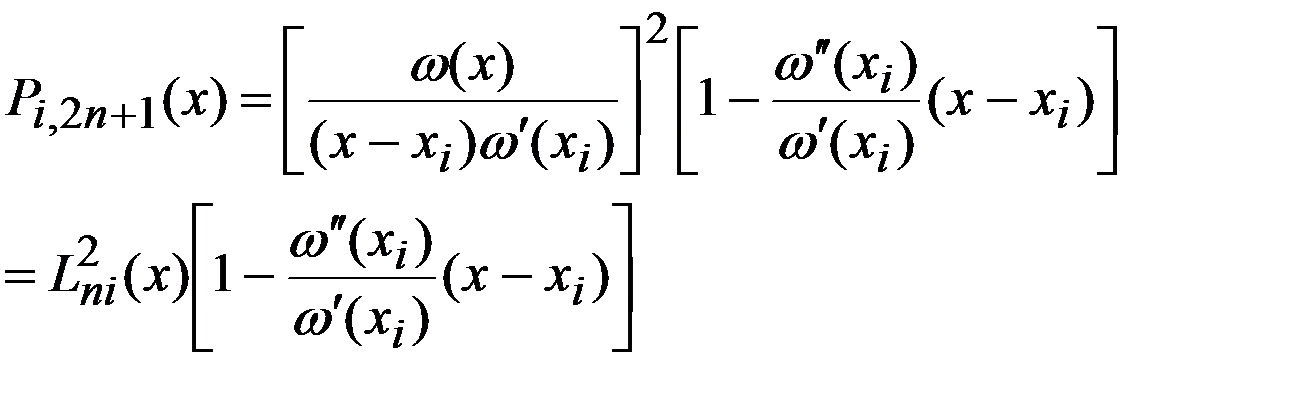 .
.
Заменим в (7) мн. 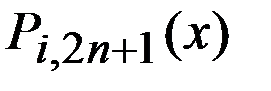 в фигурных скобках найденным выражением, тогда для мн. Эрмита с узлами кратности 2 получим окончательное выражение
в фигурных скобках найденным выражением, тогда для мн. Эрмита с узлами кратности 2 получим окончательное выражение
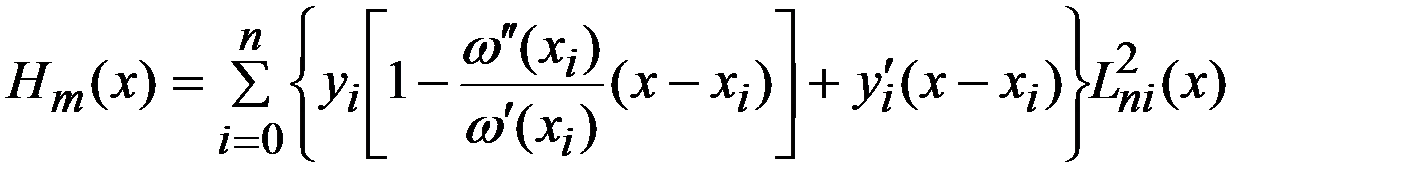 . (9)
. (9)
12. Некорректность задачи численного диф-я в пр-ве ℂ.  Примеры.Пусть ф.
Примеры.Пусть ф. 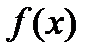 задана на
задана на 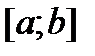 табл. знач.
табл. знач. 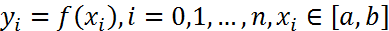 и надо найти приближ. знач. ее производной в некоторой точке этого отрезка.
и надо найти приближ. знач. ее производной в некоторой точке этого отрезка.
Решение поставленной задачи можно провести с использованием ИМ Лагранжа 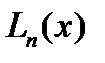 порядка n, кот. приближает ф. с погрешн.
порядка n, кот. приближает ф. с погрешн. 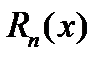 . Дифференцируя равенство
. Дифференцируя равенство 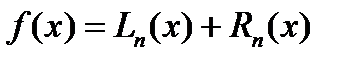 , (1)m раз имеем погрешность
, (1)m раз имеем погрешность 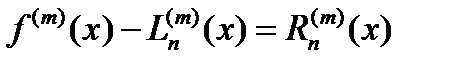 . (2)
. (2)
Т.о., производная мн. 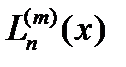 приближает производную ф.
приближает производную ф. 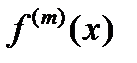 с погрешн.
с погрешн. 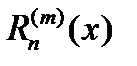 , т.е., приближенное равенство
, т.е., приближенное равенство 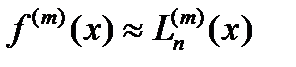 (3)имеет погрешность
(3)имеет погрешность 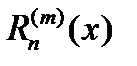 .
.
Покажем, что в общем случае малая разность между двумя ф. на отр. еще не означает, что малой будет и разность их производных на этом отр. В качестве примера рассм. ф. 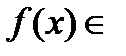 ℂ
ℂ 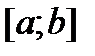 и
и 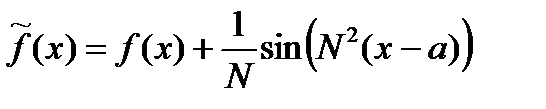 . Найдем отклонение
. Найдем отклонение 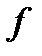 от
от 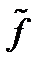 . Расстоян. между этими ф. в пр. ℂ
. Расстоян. между этими ф. в пр. ℂ 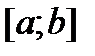 равно
равно 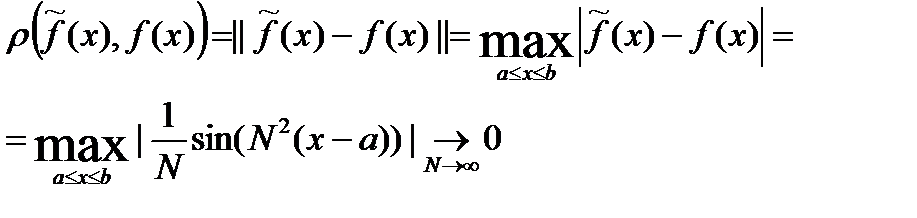
а расстояние между их производными в этом пр. 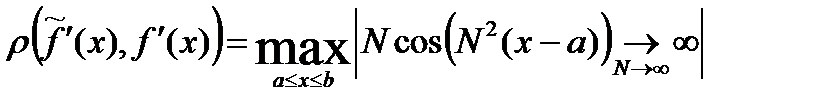 . Некорректность в пр. ℂ задачи численного дифференц. заключ. в том, что из сходимости в этом пр. последовательности ф. не следует, что последовательность производных этих ф. также будет сходиться.
. Некорректность в пр. ℂ задачи численного дифференц. заключ. в том, что из сходимости в этом пр. последовательности ф. не следует, что последовательность производных этих ф. также будет сходиться.
Примеры формул численного дифференцирования
В качестве примера рассм. использование для интерполирования в начале таблицы ИМ Ньютона:
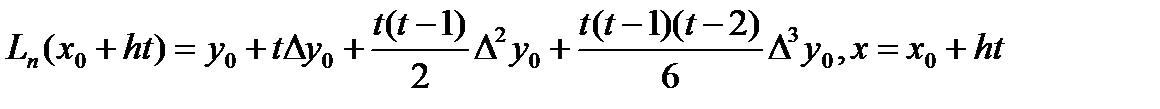 .
.
Дифф. приближенное равенство 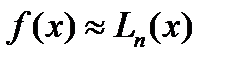 будем иметь:
будем иметь:
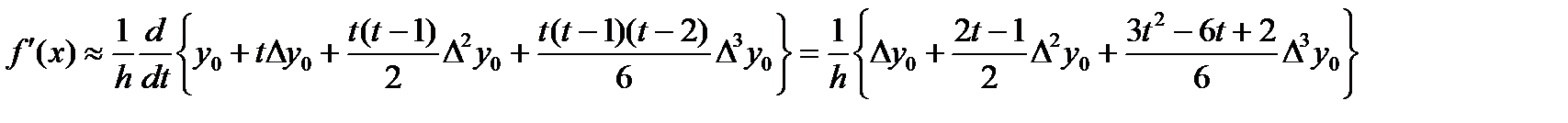 В случае
В случае 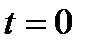 форм. приобретает вид
форм. приобретает вид 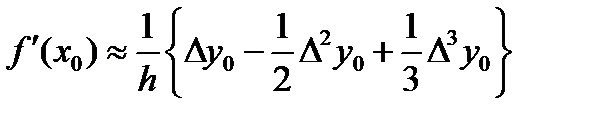 . Для второй производной получаем соотв.
. Для второй производной получаем соотв. 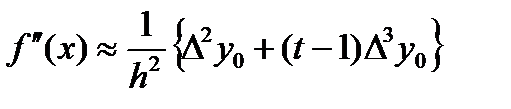 и
и 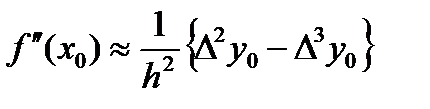 .
.
Третья производная мн. третьей степени явл. константой 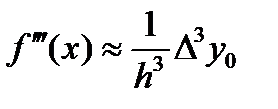 .
.
При неравноотстоящих узлах для построения форм. численного дифференц. используются ИМ Лагранжа
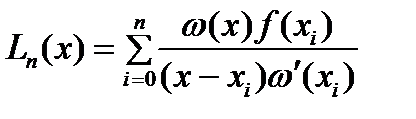 и интерпол. форм. Ньютона с РР
и интерпол. форм. Ньютона с РР
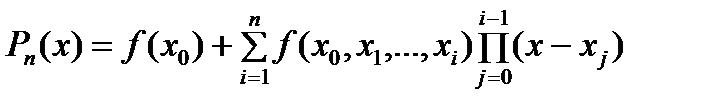 .
.
