Оценка качества парной регрессии
1. Величины стандартных ошибок коэффициентов регрессии приведены в поле Std.Error (рис. 1.1). Они показывают, насколько в среднем значение случайной величины отклоняется от его математического ожидания. В поле Prob – указывается Р-значение – вероятность того, что гипотеза о незначимости коэффициента верна.
· Для константы Р-значение равно 0,0022, что говорит о том, что коэффициент значим на уровне значимости 0,01 на уровне доверия = 99%.
· Для образования: Р-значение равно 0,0005, что говорит о том, что коэффициент значим на уровне значимости 0,01 на уровне доверия = 99%
2. Доверительные интервалы коэффициентов определяются с помощью полей Coefficient и Std.Error.
· Константа: доверительный интервал для 1% =[4860,86-1575,78*2,58; 4860,86+1575,78 *2,58] = [795,35; 8926,41]; для 5% =[4860,86-1575,78*1,96; 4860,86+1575,78 *1,96] = [1772,33; 7949,39] и для 10% =[4860,86-1575,78*1,65; 4860,86+1575,78*1,65]=[2260,823; 7460,897].
· Образование: доверительный интервал для 1% =[315,55-90,05*2,58; 315,55+90,05*2,58] = [83,22; 547,879]; для 5%=[315,55-90,05*1,96; 315,55+90,05*1,96] = [139,05;492,05] и для 10%=[315,55-90,05*1,65; 315,55+90,05*1,65] = [166,97;464,13].
3. Коэффициент детерминации приводится в поле R-squared = 0,035981. Данный показатель значит, что на 3, 6% изменение переменной salary определяется изменением переменной education, и на 96,4% изменение переменной salary определяется изменением других факторов.
4. Стандартная ошибка регрессии S (поле S.E. of regression) может сравниваться со средним значением зависимой переменной в поле Mean dependent var. Чем меньше значение S по отношению к среднему значению зависимой переменной, тем лучше качество модели. В нашем случае S = 5999,47 и Mean dependent var = 10260,51, говорит о том, что качество модели неплохое.
5. В поле Prob(F-statistic) приводится вероятность того, что гипотеза о незначимости уравнения верна. В нашем случае Prob(F-statistic) = 0,000521, значит уравнение значимо на уровне значимости 0,01 (на уровне доверия 99%).
6. Для определения средней абсолютной процентной ошибки в окне Equation нажимаем кнопку Forecast, в новом окне нажимаем OK.
В результате в окне рабочего файла появился ряд теоретических значений зависимой переменной (SALARYF), а в окне Equation отобразились графики фактических и теоретических значений зависимой переменной (рис. 1.3).
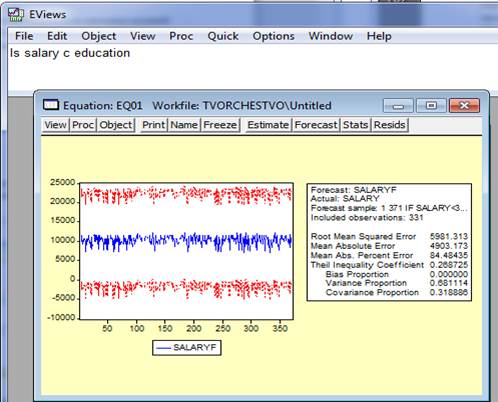
Рис. 1.3
В таблице справа значение поля Mean Abs. Percent Error и есть значение средней абсолютной процентной ошибки = 84,48,что является достаточно большим значением и указывает на плохое качество подгонки уравнения.
Проверим качество построенного уравнения регрессии. Для этого в окне Equation выбираем меню View => Actual, Fitted, Residual=> Actual, Fitted, Residual Graph. Перед нами открывается окно (рис. 1.4)
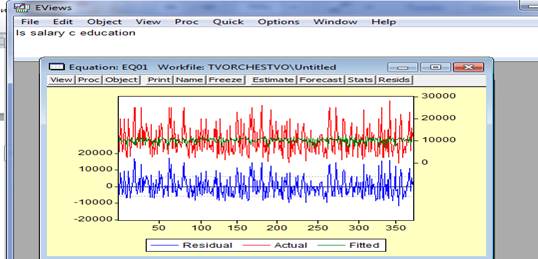
Рис. 1.4
Качество уравнения считается хорошим, если графики фактических (Actual) и прогнозных (Fitted) данных близки, и график остатков (Reaidual) показывает небольшие значения относительно значений зависимой переменной (заработной платы). Получается, что качество уравнения можно считать хорошим.
