Тема 6. Интегральное исчисление.

МАТЕМАТИКА

Семестр

Учебно-методический комплекс

Для студентов заочной формы обучения

направления «Менеджмент»

Составитель: Н.П. Дмитриев

Содержание дисциплины в 1 семестре

Тема 1. Линейная и векторная алгебра.

1. Понятие матрицы. Линейные операции над матрицами. Произведение матриц. Свойства операций сложения и произведения матриц.
2. Определители и их свойства. Правило Крамера решения систем линейных уравнений.
3. Миноры и алгебраические дополнения. Единичная и обратная матрицы. Методы решений систем линейных уравнений: метод обратной матрицы, метод Гаусса.
4. Векторы и линейные операции над ними. Скалярное произведение. Длина вектора. Прямоугольная система координат на плоскости и в трехмерном пространстве. Разложение вектора по координатным ортам. Угол между векторами. Условия коллинеарности и перпендикулярности векторов.
5. Векторное и смешанное произведения векторов, их геометрический смысл. N-мерные векторы, линейная зависимость векторов, базис векторного пространства.

Тема 2. Аналитическая геометрия

1. Прямая на плоскости. Описание прямой, проходящей через заданную точку и с заданным наклоном. Прямая, проходящая через две точки. Общее уравнение прямой на плоскости. Условие параллельности и перпендикулярности прямых. Уравнение прямой в отрезках. Расстояние от точки до прямой.
2. Плоскости и прямые в трехмерном пространстве. Векторное описание плоскости, проходящей через заданную точку перпендикулярно заданному вектору. Общее уравнение плоскости. Условия параллельности и перпендикулярности плоскостей.
3. Общее описание прямой в пространстве. Канонические уравнения прямой. Взаимное расположение прямых и плоскостей в пространстве и их аналитическая характеристика.
4. Кривые на плоскости. Геометрические объекты второго порядка (эллипс, гипербола, парабола). Специальные кривые (кардиоиды, лемнискаты, циклоиды…).
5. Поверхности в пространстве. Геометрические объекты второго порядка (эллипсоид, гиперболоид, параболоид).

Тема 3. Введение в анализ.

1. Числовые функции. Их способы задания и классификация.
2. Предел числовой последовательности. Предельный переход в арифметических операциях и неравенствах. Признаки существования предела для промежуточных и монотонных последовательностей. Число е.
3. Два равносильных определения предела числовой функции в точке. Арифметические свойства операции предельного перехода. Замечательные пределы. Сравнение функций.
4. Непрерывные функции. Непрерывность основных элементарных функций. Точки разрыва и их классификация. Теоремы об экстремальных и промежуточных значениях непрерывных функций.

Тема 4. Дифференциальное исчисление.

1. Три основных понятия дифференциального исчисления функции одного переменного (производная, дифференцируемость, дифференциал) и их интерпретации в физике, геометрии, экономике и др.
2. Формулы дифференцирования арифметических операций, сложной и обратной функций.
3. Производные и дифференциал высших порядков. Формула Тейлора.
4. Основные теоремы дифференциального исчисления (Ферма, Ролля, Лагранжа, Коши).
5. Приложение дифференциального исчисления к исследованию качественных свойств числовых функций.
6. Асимптоты графика функции. Правило Лопиталя. Схема исследования функций.

Тема 5. Функции многих переменных.

1. Функции многих переменных. Понятие их предела и непрерывности. Частные производные, дифференцируемость и дифференциал. Высшее дифференцирование. Формулы дифференцирования неявных функций.
2. Необходимые и достаточные условия локального экстремума функции многих переменных.
3. Условный экстремум. Метод множителей Лагранжа.

Тема 6. Интегральное исчисление.

1. Первообразная и неопределенный интеграл. Простейшие свойства неопределенного интегрирования. Таблица интегралов.
2. Методы замены переменного и интегрирования по частям. Интегрирование рациональных и иррациональных функций.
3. Определённый интеграл и его свойства. Теорема о среднем значении. Интеграл с переменным верхним пределом. Условия его непрерывности и дифференцируемости. Формула Ньютона-Лейбница.
4. Замена переменной и интегрирование по частям в определенном интеграле. Несобственные интегралы. Приложения определенного интеграла.

Вопросы к экзамену в 1 семестре

1) Матрицы. Понятие матрицы. Линейные операции над матрицами и их свойства

2) Произведение матриц. Свойства произведения матриц.

3) Определители и их свойства. Правило Крамера.

4) Единичная и обратная матрицы. Решение СЛАУ матричным методом.

5) Решение СЛАУ методом Гаусса.

6) Решение СЛАУ методом Гаусса-Жордана.

7) Векторы, действия над ними. Координаты вектора (теорема о базисе плоскости).

8) Скалярное произведение векторов. Свойства и геометрические приложения.

9) Расстояние между точками. Деление отрезка в данном отношении.

10) Векторы в пространстве (теорема о базисе пространства).

11) Векторное произведение векторов. Свойства и геометрические приложения.

12) Смешанное произведение векторов. Свойства и геометрические приложения.

13) Прямая на плоскости. Прямая, проходящая через две точки.

14) Описание прямой, проходящей через заданную точку и с заданным угловым коэффициентом. Условие параллельности и перпендикулярности прямых.

15) Общее уравнение прямой на плоскости. Условие параллельности и перпендикулярности прямых. Уравнение прямой в отрезках.

16) Угол между прямыми. Расстояние от точки до прямой.

17) Плоскость в пространстве. Взаимное расположение плоскостей в пространстве

18) Линии второго порядка на плоскости и их общее описание.

19) Каноническое уравнение эллипса, геометрическая характеристика, построение.

20) Каноническое уравнение гиперболы, геометрическая характеристика, построение.

21) Каноническое уравнение параболы, геометрическая характеристика, построение.

22) Прямые в трехмерном пространстве.

23) Векторное описание плоскости, проходящей через заданную точку перпендикулярно заданному вектору.

24) Векторное описание плоскости, проходящей через три точки.

25) Условия параллельности и перпендикулярности плоскостей.

26) Общее уравнение поверхности. Цилиндрическая поверхность.

27) Эллипсоид, гиперболоид, параболоид, конус

28) Множества и действия над ними.

29) Элементарные функции. Свойства. Графики. Преобразование графиков.

30) Предел функции в точке. Раскрытие неопределенностей.

31) Замечательные пределы.

32) Непрерывность функции в точке.

33) Непрерывность функции на отрезке.

34) Производная функции, её геометрический смысл.

35) Правила дифференцирования. Таблица производных.

36) Основные теоремы дифференциального исчисления (Ферма, Ролля, Лагранжа, Коши).

37) Исследование функции на монотонность и экстремумы.

38) Нахождение направлений выпуклости и точек перегиба графика функции.

39) Правило Лопиталя.

40) Асимптоты графика функции.

41) Формула Тейлора и ее применение.

42) Функция двух переменных, её область определения и график.

43) Частные производные функции двух переменных.

44) Экстремум функции двух переменных: необходимое условие, достаточное условие существования.

45) Условный экстремум. Задача Дидоны. Функция Лагранжа.

46) Глобальный экстремум функции двух переменных в замкнутой области.

47) Неопределённый интеграл и его свойства.

48) Таблица неопределённых интегралов.

49) Метод замены переменной в неопределённом интеграле.

50) Формула интегрирования по частям в неопределённом интеграле.

51) Интегрирование рациональных дробей.

52) Интегрирование некоторых трансцендентных функций.

53) Определённый интеграл и его свойства. Формула Ньютона – Лейбница.

54) Геометрические приложения определённого интеграла.

3. Варианты контрольных заданий

Инструкция к оформлению

1. Контрольную работу (КР1) оформлять в отдельной школьной тетрадке с указанием ФИО студента и номера группы

2. Каждая КР выполняется согласно выбранному варианту. Номер варианта соответствует номеру фамилии студента в списке студенческой группы

3. Все задачи должны быть решены четко и ясно со ссылками на известные теоремы и формулы

4. В конце работы проставляется дата и подпись

5. В случае, если КР не зачтена, делается работа над ошибками и она снова отправляется на проверку преподавателю

Тексты контрольных заданий №1

1. Разложить вектор X по векторам P, Q, R. Систему решить 1) методом Крамера, 2) матричным методом, 3) методом Гаусса

2. Треугольник АВС задан своими вершинами А, B, C. Найти: 1) уравнения сторон, 2) уравнение и длину высоты из точки А на сторону ВС, 3) площадь треугольника

3. Тетраэдр АВСD задан своими вершинами А, B, C, D. Найти: 1) уравнения граней, 2) уравнение средней линии грани АВС, 3) объем тетраэдра

4. Найти пределы функций

5. Исследовать функции и построить график

№ зад	Вариант 0
	X=(1,7,1) P(-1,0,2) Q(0,-2,1) R(3,1,0)
	A(2,1) B(4,-3) C(-3,0)
	A(2,1,4) B(-2,1,0) C(0,-3,-5) D(1,0,-3)

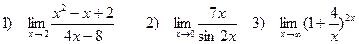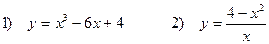№ зад	Вариант 1
	X=(4,-3,4) P(0,1,2) Q(1,1,0) R(3,-1,1)
	A(3,1) B(4,-1) C(-3,5)
	A(1,1,4) B(-2,3,0) C(0,-3,-1) D(4,0,-3)

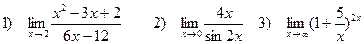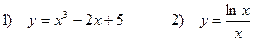№ зад	Вариант 2
	X=(-2,2,3) P(-1,0,2) Q(0,-2,1) R(3,1,0)
	A(3,0) B(4,-2) C(-4,6)
	A(-1,1,4) B(-1,3,0) C(0,-4,-1) D(4,0,-5)

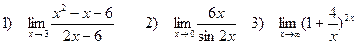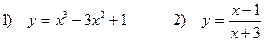№ зад	Вариант 3
	X=(6,0,6) P(0,1,2) Q(1,1,0) R(3,-1,1)
	A(3,0) B(4,-1) C(-4,1)
	A(2,1,5) B(-4,3,0) C(0,-2,-1) D(4,0,-4)

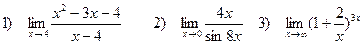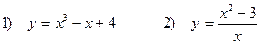№ зад	Вариант 4
	X=(9,-1,2) P(-1,0,2) Q(0,-2,1) R(3,1,0)
	A(3,-2) B(4,-1) C(-3,6)
	A(1,-1,4) B(-2,3,0) C(0,-3,1) D(4,0,-2)

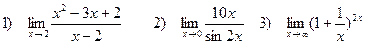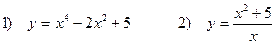№ зад	Вариант 5
	X=(4,-3,4) P(0,1,2) Q(1,1,0) R(3,-1,1)
	A(3,1) B(4,-1) C(-3,5)
	A(1,1,4) B(-2,3,0) C(0,-3,-1) D(4,0,-3)

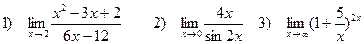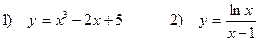№ зад	Вариант 6
	X=(-5,2,2) P(-1,0,2) Q(0,-2,1) R(3,1,0)
	A(3,0) B(4,-2) C(-4,6)
	A(-1,1,4) B(-1,3,0) C(0,-4,-1) D(4,0,-5)

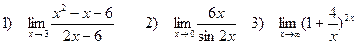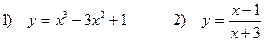№ зад	Вариант 7
	X=(3,1,5) P(0,1,2) Q(1,1,0) R(3,-1,1)
	A(3,0) B(4,-1) C(-4,1)
	A(2,1,5) B(-4,3,0) C(0,-2,-1) D(4,0,-4)

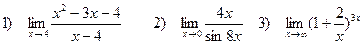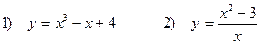№ зад	Вариант 8
	X=(-5,-7,7) P(-1,0,2) Q(0,-2,1) R(3,1,0)
	A(3,-2) B(4,-1) C(-3,6)
	A(1,-1,4) B(-2,3,0) C(0,-3,1) D(4,0,-2)

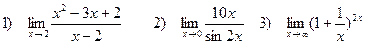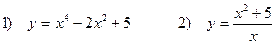№ зад	Вариант 9
	X=(4,-3,4) P(0,1,2) Q(1,1,0) R(3,-1,1)
	A(3,1) B(4,-1) C(-3,5)
	A(1,1,4) B(-2,3,0) C(0,-3,-1) D(4,0,-3)

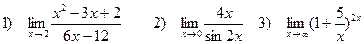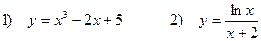№ зад	Вариант 10
	X=(4,-2,-1) P(-1,0,2) Q(0,-2,1) R(3,1,0)
	A(3,0) B(4,-2) C(-4,6)
	A(-1,1,4) B(-1,3,0) C(0,-4,-1) D(4,0,-5)

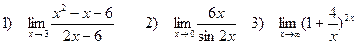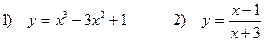№ зад	Вариант 11
	X=(4,-1,-1) P(0,1,2) Q(1,1,0) R(3,-1,1)
	A(3,0) B(4,-1) C(-4,1)
	A(2,1,5) B(-4,3,0) C(0,-2,-1) D(4,0,-4)

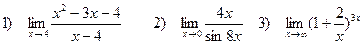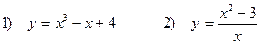№ зад	Вариант 12
	X=(-4,1,1) P(-1,0,2) Q(0,-2,1) R(3,1,0)
	A(3,-2) B(4,-1) C(-3,6)
	A(1,-1,4) B(-2,3,0) C(0,-3,1) D(4,0,-2)

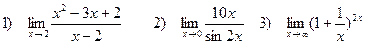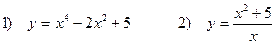№ зад	Вариант 13
	X=(4,-3,4) P(0,1,2) Q(1,1,0) R(3,-1,1)
	A(3,1) B(4,-1) C(-3,5)
	A(1,1,4) B(-2,3,0) C(0,-3,-1) D(4,0,-3)

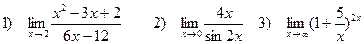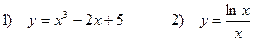№ зад	Вариант 14
	X=(-5,-7,7) P(-1,0,2) Q(0,-2,1) R(3,1,0)
	A(3,0) B(4,-2) C(-4,6)
	A(-1,1,4) B(-1,3,0) C(0,-4,-1) D(4,0,-5)

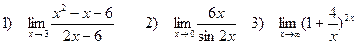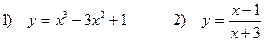№ зад	Вариант 15
	X=(7,0,4) P(0,1,2) Q(1,1,0) R(3,-1,1)
	A(3,0) B(4,-1) C(-4,1)
	A(2,1,5) B(-4,3,0) C(0,-2,-1) D(4,0,-4)

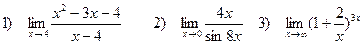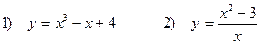№ зад	Вариант 16
	X=(4,-2,6) P(-1,0,2) Q(0,-2,1) R(3,1,0)
	A(3,-2) B(4,-1) C(-3,6)
	A(1,-1,4) B(-2,3,0) C(0,-3,1) D(4,0,-2)

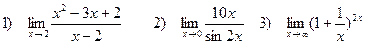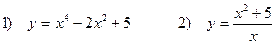№ зад	Вариант 17
	X=(4,5,2) P(0,1,2) Q(1,1,0) R(3,-1,1)
	A(3,0) B(4,-2) C(-4,6)
	A(-1,1,4) B(-1,3,0) C(0,-4,-1) D(4,0,-5)

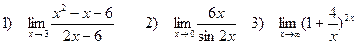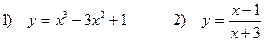№ зад	Вариант 18
	X=(-5,-2,11) P(-1,0,2) Q(0,-2,1) R(3,1,0)
	A(3,0) B(4,-1) C(-4,1)
	A(2,1,5) B(-4,3,0) C(0,-2,-1) D(4,0,-4)

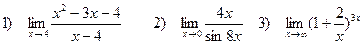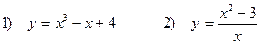№ зад	Вариант 19
	X=(1,3,4) P(0,1,2) Q(1,1,0) R(3,-1,1)
	A(3,-2) B(4,-1) C(-3,6)
	A(1,-1,4) B(-2,3,0) C(0,-3,1) D(4,0,-2)

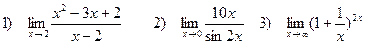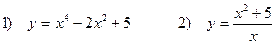№ зад	Вариант 20
	X=(2,1,2) P(-1,0,2) Q(0,-2,1) R(3,1,0)
	A(3,1) B(4,-1) C(-3,5)
	A(1,1,4) B(-2,3,0) C(0,-3,-1) D(4,0,-3)

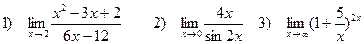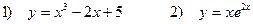№ зад	Вариант 21
	X=(1,2,2) P(0,1,2) Q(1,1,0) R(3,-1,1)
	A(3,0) B(4,-2) C(-4,6)
	A(-1,1,4) B(-1,3,0) C(0,-4,-1) D(4,0,-5)

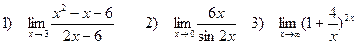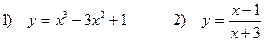№ зад	Вариант 22
	X=(-5,-7,7) P(-1,0,2) Q(0,-2,1) R(3,1,0)
	A(3,0) B(4,-1) C(-4,1)
	A(2,1,5) B(-4,3,0) C(0,-2,-1) D(4,0,-4)

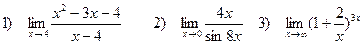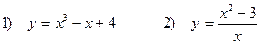№ зад	Вариант 23
	X=(4,-3,4) P(0,1,2) Q(1,1,0) R(3,-1,1)
	A(3,-2) B(4,-1) C(-3,6)
	A(1,-1,4) B(-2,3,0) C(0,-3,1) D(4,0,-2)

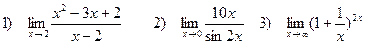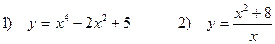№ зад	Вариант 24
	X=(2,-1,3) P(-1,0,2) Q(0,-2,1) R(3,1,0)
	A(3,1) B(4,-1) C(-3,5)
	A(1,1,4) B(-2,3,0) C(0,-3,-1) D(4,0,-3)

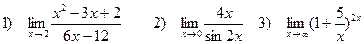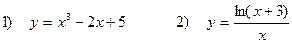№ зад	Вариант 25
	X=(4,1,3) P(0,1,2) Q(1,1,0) R(3,-1,1)
	A(3,0) B(4,-2) C(-4,6)
	A(-1,1,4) B(-1,3,0) C(0,-4,-1) D(4,0,-5)

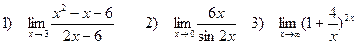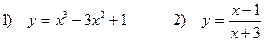№ зад	Вариант 26
	X=(-5,-7,7) P(3,1,0) Q(0,-2,1) R(-1,0,2)
	A(3,0) B(4,-1) C(-4,1)
	A(2,1,5) B(-4,3,0) C(0,-2,-1) D(4,0,-4)

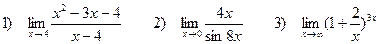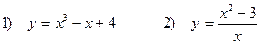№ зад	Вариант 27
	X=(4,-3,4) P(1,1,0) Q(0,1,2) R(3,-1,1)
	A(3,-2) B(4,-1) C(-3,6)
	A(1,-1,4) B(-2,3,0) C(0,-3,1) D(4,0,-2)

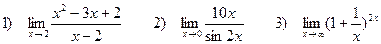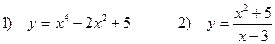№ зад	Вариант 28
	X=(-5,7-,7) P(0,1,-2) Q(3,0,1) R(-1,2,0)
	A(3,1) B(4,-1) C(-3,5)
	A(1,1,4) B(-2,3,0) C(0,-3,-1) D(4,0,-3)

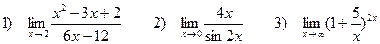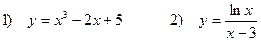№ зад	Вариант 29
	X=(-3,4,4) P(1,0,2) Q(1,1,0) R(-1,3,1)
	A(3,0) B(4,-2) C(-4,6)
	A(-1,1,4) B(-1,3,0) C(0,-4,-1) D(4,0,-5)

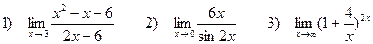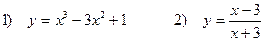№ зад	Вариант 30
	X=(-7,-5,7) P(0,-1,2) Q(-2,0,1) R(1,3,0)
	A(3,0) B(4,-1) C(-4,1)
	A(2,1,5) B(-4,3,0) C(0,-2,-1) D(4,0,-4)

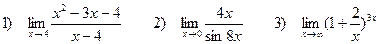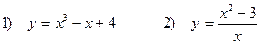№ зад	Вариант 31
	X=(4,-3,4) P(0,1,2) Q(1,1,0) R(3,-1,1)
	A(3,-2) B(4,-1) C(-3,6)
	A(1,-1,4) B(-2,3,0) C(0,-3,1) D(4,0,-2)

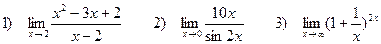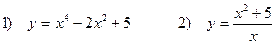№ зад	Вариант 32
	X=(-5,-7,7) P(-1,0,2) Q(0,-2,1) R(3,1,0)
	A(3,-2) B(4,-1) C(-3,6)
	A(1,-1,4) B(-2,3,0) C(0,-3,1) D(4,0,-2)

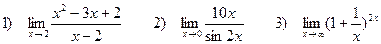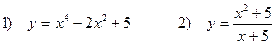№ зад	Вариант 33
	X=(5,-3,9) P(3,-1,0) Q(0,-2,1) R(-1,0,-2)
	A(3,5) B(4,-1) C(-4,2)
	A(-2,1,5) B(-4,-3,0) C(0,2,-1) D(4,0,6)

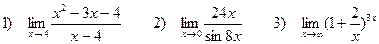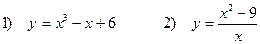Решение варианта 0 контрольной работы №1

Задача 1. Разложение вектора X=(1,7,1) по векторам P(-1,0,2), Q(0,-2,1,) R(3,1,0) имеет вид:

X=άP+βQ+γR

Распишем это векторное уравнение покоординатно, т.е. сначала приравняем абсциссы, затем ординаты, а потом аппликаты. В результате получим систему трех линейных алгебраических уравнений с тремя неизвестными ά, β, γ:

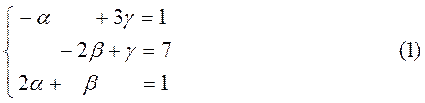
1) Решим систему (1) методом Крамера. Для этого подсчитаем 4 определителя: главный ∆ и 3 вспомогательных ∆_ά, ∆_β, ∆_γ. Напомним, что главный определитель составляется из коэффициентов при неизвестных ά, β, γ. Вспомогательные определители формируются из главного заменой соответствующего столбца столбцом свободных членов.

Главный определитель вычислим методом Лапласа с помощью разложения, например, по первой строке:

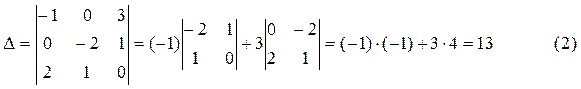
Аналогично вычисляются вспомогательные определители.

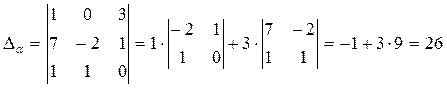
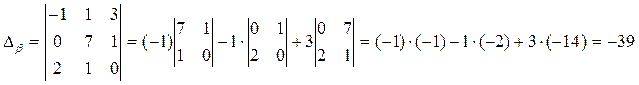
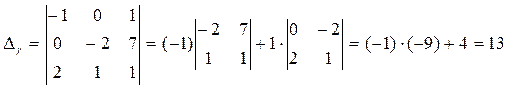
Неизвестные ά, β, γ находятся как отношения соответствующих вспомогательных определителей к главному:

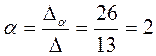
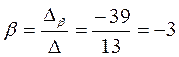
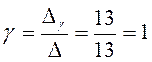
2) Решим систему (1) матричным методом. Очевидно, что

X=A^-1B,

где A^-1 – обратная матрица по отношению к матрице коэффициентов системы, B – столбец свободных членов.

Найдем обратную матрицу по схеме:

A → A^* → (A^*)^T → (A^*)^T/∆=A^-1

где A – исходная матрица,

A^* - присоединенная матрица (состоящая из алгебраических дополнений каждого элемента исходной матрицы),

(A^*)^T – транспонированная матрица относительно присоединенной матрицы A^*,

∆ - определитель матрицы А

Напомним, что для нахождения присоединенной матрицы необходимо отыскать алгебраические дополнения всех элементов исходной матрицы. Алгебраическое дополнение элемента матрицы – это определитель, получающийся вычеркиванием строки и столбца, на пересечении которых находится данный элемент. Знак такого определителя меняется на противоположный, если сумма номеров строки и столбца нечетна.

Алгебраическим дополнением элемента (-1), находящегося на пересечении первой строки и первого столбца, является определитель

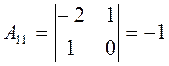
Алгебраическим дополнением элемента 0, находящегося на пересечении первой строки и второго столбца, является определитель

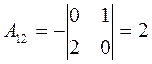
Знак определителя изменен на противоположный, так как 1+2=3 – нечетное число.

Аналогично отыскиваются алгебраические дополнения других элементов исходной матрицы.

Итак,

В результате транспонирования получаем

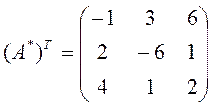
Определитель исходной матрицы был подсчитан ранее, а именно (см. формулу (2)), ∆=13. Таким образом,

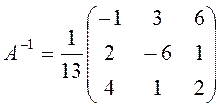
Умножая справа на столбец свободных членов, находим

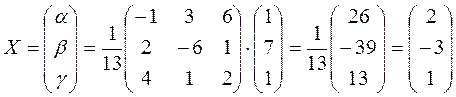
или ά=2, β=-3, γ=1.

Решим систему методом Гаусса. Составим расширенную матрицу

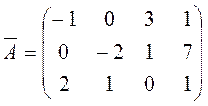
Пусть разрешающим элементом будет a₂₃=1, а разрешающей строкой – вторая строка. С помощью выбранной второй строки элементарными преобразованиями исключим переменную γ, т.е. добьемся того, чтобы все элементы третьего столбца, кроме разрешающего, оказались равными 0. А именно, если к первой строке добавить вторую, умноженную на (-3), то получим

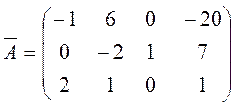
Пусть теперь разрешающим элементом будет a₃₂=1, а разрешающей строкой – третья строка. С помощью выбранной третьей строки элементарными преобразованиями исключим переменную β, т.е. добьемся того, чтобы все элементы второго столбца, кроме разрешающего, оказались равными 0. А именно, если к первой строке добавить третью, умноженную на (-6), а ко второй – третью, умноженную на 2, то получим

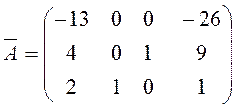
Сократим все элементы первого столбца на (-13):

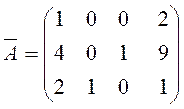
Выберем в качестве разрешающего элемент a₁₁=1. Прибавим ко второй строке первую, умноженную на (-4), а к третьей – первую, умноженную на (-2). После такого преобразования получаем

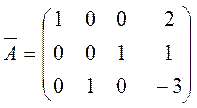
Отсюда снова получаем ά=2, β=-3, γ=1.

Итак, разложение вектора X=(1,7,1) по векторам P(-1,0,2), Q(0,-2,1,) R(3,1,0) имеет вид:

X=2P-3Q+R

Задача 2. Треугольник АВС задан своими вершинами

А(2,1), B(4,-3), C(-3,0).

1) Найдем уравнение стороны АВ, для чего воспользуемся уравнением прямой, проходящей через две точки:

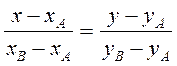
Подставляя координаты точек А и В, получаем уравнение:

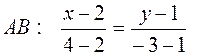
Итак, каноническое уравнение прямой АВ имеет вид:

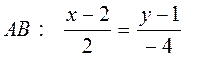
Приведем это уравнение к общему виду. По правилу пропорции получаем:

-4(x-2)=2(y-1). Раскрывая скобки, приходим к общему уравнению прямой АВ:

2x+y=5

Изолируем y и получим уравнение прямой с угловым коэффициентом:

y=-2x+5

Аналогично находятся уравнения других сторон. Каноническое уравнение прямой ВС:

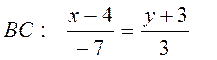
Общее уравнение прямой ВС:

3x+7y+9=0

Уравнение прямой ВС с угловым коэффициентом:

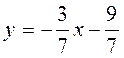
Каноническое уравнение прямой АС:

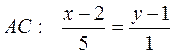
Общее уравнение прямой АС:

x-5y+3=0

Уравнение прямой АС с угловым коэффициентом:

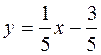
2) Найдем уравнение и длину высоты AD из точки А на сторону ВС. Из канонического уравнения стороны ВС получаем направляющий вектор

q_ВС=(-7, 3)

Этот вектор можно принять в качестве нормального вектора прямой AD:

n_AD=(-7, 3)

Следовательно, уравнение прямой AD, проходящей через точку А и имеющей нормальный вектор n_AD, имеет вид:

-7(x-2)+3(y-1)=0

Раскроем скобки и приведем к общему виду:

-7x+3y+11=0

Уравнение медианы AD в явной форме имеет вид:

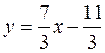
Далее найдем координаты точки D, для чего необходимо совместно решить уравнения прямой ВС и медианы AD:

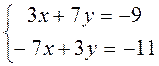
Решим эту систему методом Гаусса (алгебраического сложения). Умножим первое уравнение на 7, а второе на 3. После сложения этих уравнений переменная x исключается, что позволяет найти y. А именно,

y=-48/29

Теперь умножим первое уравнение на -3, а второе на 7. После сложения этих уравнений переменная y исключается, что позволяет найти x. А именно,

x=25/29

Проверим правильность решения системы линейных уравнений с помощью пакета символьных преобразований Maple:

> first:=-7*x+3*y=-11:

> second:=3*x+7*y=-9:

> sys:={first,second};

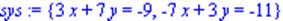
> solve(sys);

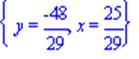
Итак, D(25/29, -48/29). Длину медианы AD находим по формуле расстояния между двумя точками:

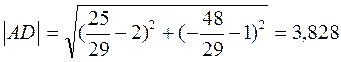
3) Для вычисления площади треугольника найдем длину стороны ВС:

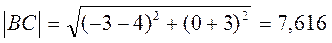
Тогда площадь треугольника ABC равна

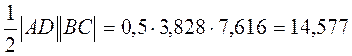
Задача 3. Тетраэдр АВСD задан своими вершинами

А(2,1 4), B(-2,1,0), C(0,-3,-5), D(1,0,-3).

1) Найдем уравнение грани ABC через смешанное произведение векторов AB, AC и AM, где М(x,y,z) – произвольная точка грани:

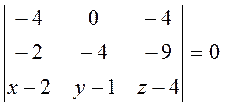
Разлагая определитель по третьей строке, получаем

-16(x-2)-28(y-1)+16(z-4)=0

или

ABC: 4x+7y-4z+1=0

Аналогично находятся уравнения других граней.

2) Уравнение средней линии грани АВС будем искать в следующей последовательности: сначала вычислим координаты точек P, Q – середин сторон АВ и АС. А именно, по формулам

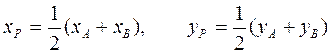
находим: P(0,1,2). По аналогичным формулам Q(1,-1,-0.5). Уравнение средней линии PQ запишем в канонической форме:

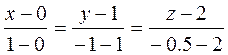
или

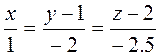
3) Объем тетраэдра вычислим по формуле

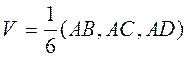
где (AB,AC,AD) – смешанное произведение этих трех векторов. Итак,

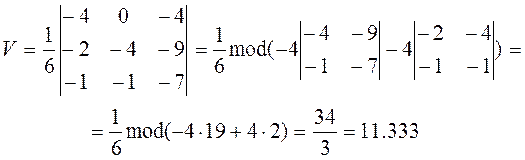
Задача 4. Найти пределы функций:

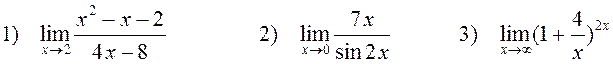
1) Сначала подставим предельную точку x=2: числитель и знаменатель дроби равны нулю. Значит, мы имеем неопределенность первого типа 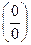. По теореме Виета или через дискриминант найдем корни квадратичной формы в числителе и разложим ее на линейные множители:

x²-x-2=(x-2)(x+1)

Теперь предел можно записать так:

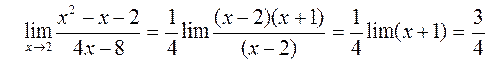
2) Воспользуемся таблицей эквивалентных бесконечно малых, а именно,

sin2x~2x

(Это следствие из первого замечательного предела)

Тогда

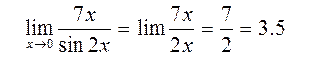
Решим эту же задачу по правилу Лопиталя. Напомним, что по этому правилу отношение дифференцируемых бесконечно малых можно заменить отношением их производных. Тогда

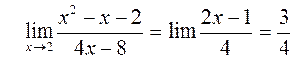
3) Сделаем следующие преобразования:

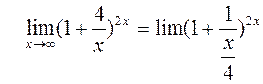
Обозначим v=x/4 и снова воспользуемся таблицей эквивалентных бесконечно малых, а именно,

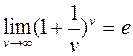
(Это второй замечательный предел).

Тогда

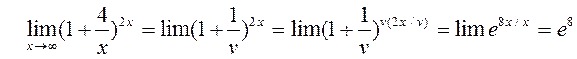
Задача 5. Исследовать функции и построить графики

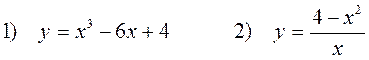
Исследование функций проведем по следующей схеме:

А) общие характеристики

· область определения

· нули

· четность

· периодичность

· особые точки

· асимптоты

В) дифференциальные характеристики

· монотонность

· экстремумы

· выпуклость

· перегибы

1) Рассмотрим сначала функцию

· область определения – вся числовая прямая: D(y)=R

· нули – точки, в которых значение функции равно нулю. Очевидно, что один корень x₁=2. Разделим (например, уголком) кубическую форму в правой части функции на линейный множитель (x-2) для отыскания еще двух других корней. Получим

x³-6x+4=(x-2)(x²+2x-2)

Квадратичная форма x²+2x-2 (по теореме Виета или через дискриминант) имеет два корня x₂=-1-√3, x₃=-1+√3. Таким образом,

D₀={-1-√3, -1+√3, 2}

· Очевидно, что это функция общего вида, т.е. не обладает свойством четности

y(x) = y(-x)

или нечетности

y(x) = - y(-x)

· Функция не является периодической, т.е. не найдется такого Т, что

y(x)=y(x+Т)

· Особые точки: y(0)=4. Значит, график функции пересекает ось ординат в точке (0,4).

· Вертикальных асимптот нет, так как функция не имеет точек существенного разрыва (разрыва второго рода) хотя бы с одним односторонним бесконечным пределом. Убедимся, что нет и наклонных асимптот. Действительно, угловой коэффициент асимптоты равен

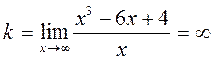
· Исследуем функцию на монотонность. Для этого вычислим критические точки первого рода, т.е. точки, в которых производная равна нулю или не существует. Найдем производную

y^’=3x²-6

и приравняем нулю:

x²-2=0.

Критические точки: -√2, √2. Они делят область определения на три участка монотонности:

D=(-∞, -√2)U(-√2, √2)U(√2, ∞)

Исследуем направление монотонности с помощью таблицы

x	(-∞, -√2)	(-√2, √2)	(√2, ∞)
y’	+	-	+
y	↑	↓	↑

Итак, участки монотонности:

(-∞, -√2) – участок возрастания функции

(-√2, √2) – участок убывания функции

(√2, ∞) - участок возрастания функции

· Из таблицы легко определить точки экстремума. А именно, x=-√2 – точка локального максимума функции, а x=√2 – точка локального минимума функции

· Исследуем функцию на выпуклость. Для этого вычислим критические точки второго рода, т.е. точки, в которых производная второго порядка равна нулю или не существует. Найдем производную второго порядка

y^’’=6x

Приравнивая нулю, получаем одну точку x=0. Она делит область определения функции на два участка:

D=(-∞, 0)U(0, ∞)

Исследуем направление выпуклости с помощью таблицы

x	(-∞, 0)	(0, ∞)
y’’	-	+
y	∩	U

Итак, участки выпуклости:

(-∞, 0) – участок выпуклости вверх

(0, ∞) - участок выпуклости вниз

· Из таблицы легко определить точку перегиба. А именно, x=0 – точка перегиба функции

Используя полученную информацию, построим график заданной функции с помощью пакета Maple.

plot(x^3-6*x+4,x=-3..3);

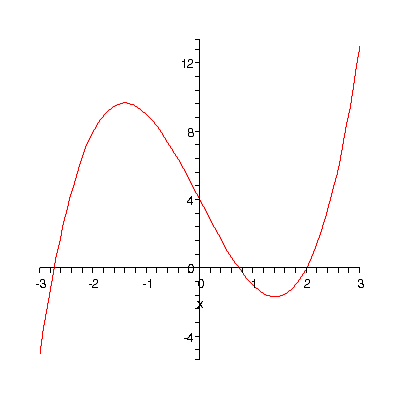
2) Рассмотрим теперь функцию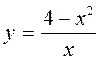

· область определения – все точки числовой прямой, за исключением точки x=0: D(y)=R\{0}

· нули – точки, в которых значение функции равно нулю.Приравнивая нулю числитель, получаем

D₀={-2, 2}

· Очевидно, что это нечетная функция. В самом деле,

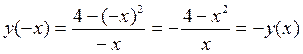
Значит, график функции симметричен относительно начала координат.

· Функция также не является периодической, т.е. не найдется такого Т, что

y(x)=y(x+Т)

· Особые точки: x=0. Найдем односторонние пределы в этой точке:

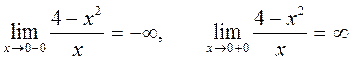
· Полученные значения односторонних пределов позволяются сделать вывод, что функция имеет вертикальную асимптоту x=0. Убедимся, что функция имеет и наклонную асимптоту y=kx+b. Действительно,

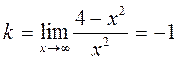
Следовательно, y=-x+b. Найдем параметр b.

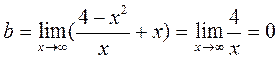
Итак, наклонная асимптота заданной функции такова: y=-x

· Исследуем функцию на монотонность. Для этого вычислим критические точки первого рода. Найдем производную

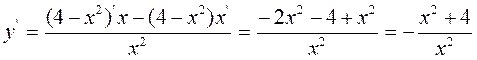
Проверим правильность дифференцирования в среде Maple:

> diff((4-x^2)/x,x);

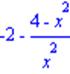
Критическая точка: 0. Она не входит в область определения функции, но является граничной для нее. Область определения в этом случае естественным образом представляется объединением двух участков монотонности:

D=(-∞,0)U(0, ∞)

Исследуем направление монотонности с помощью таблицы

x	(-∞, 0)	(0, ∞)
y’	-	-
y	↓	↓

Итак, участки монотонности:

(-∞, 0) – участок убывания функции

(0, ∞) - участок убывания функции

· Из таблицы видно, что экстремумов функция не имеет

· Исследуем функцию на выпуклость. Для этого вычислим критические точки второго рода. Найдем производную второго порядка

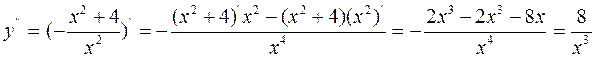
Критическая точка: x=0. Она делит область определения функции на те же два участка:

D=(-∞, 0)U(0, ∞)

Исследуем направление выпуклости с помощью таблицы

x	(-∞, 0)	(0, ∞)
y’’	-	+
y	∩	U

Итак, участки выпуклости:

(-∞, 0) – участок выпуклости вверх

(0, ∞) - участок выпуклости вниз

· Точка x=0 не является точкой перегиба, так как она не входит в область определения функции и в ней не существует производная второго порядка.

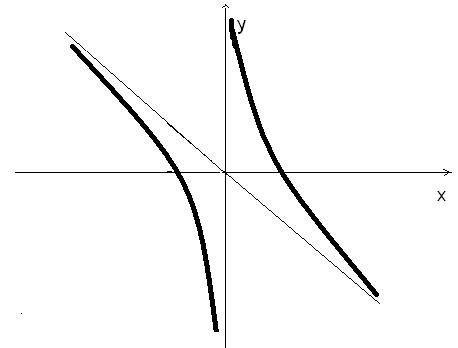
Используя полученную информацию, построим график заданной функции

Литература

Основная литература

1. Бугров А.Г., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – М.: Наука, 1984

2. Бугров А.Г., Никольский С.М. Дифференциальное и интегральное исчисление. – М.: Наука, 1980

3. Бугров А.Г., Никольский С.М. Задачник. – М.: Наука, 1984

4. Высшая математика для экономистов / под ред. проф. Кремера Н.Ш. – М.: ЮНИТИ, 1997

5. Общий курс высшей математики для экономистов / под ред. проф. В.И.Ермакова. – М.: Инфра-М, 2005

6. Сборник задач по высшей математике для экономистов / под ред. проф. В.И.Ермакова. – М.: Инфра-М, 2002

7. Шипачев В.С. Высшая математика. – М.: ВШ, 2000

1. Шипачев В.С. Задачник по высшей математике. – М.: ВШ, 2001

Дополнительная литература

1. Воронов М.В., Мещеряков Г.П. Высшая математика для экономистов и менеджеров. – Ростов-на-Дону, ФЕНИКС, 2004

2. Высшая математика. Общий курс / под ред. А.И.Яблонского. – Минск: ВШ, 1993

3. Головина Л.И. Линейная алгебра и некоторые ее приложения. – М.: Наука, 1985

4. Гусак А.А. Высшая математика. – Мн.: ТетраСистемс, 1998. – т.1,2

5. Гусак А.А. Задачи и упражнения по высшей математике. – Мн.: Выш.шк., 1988. – т.1,2

6. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М.: ВШ, 1986. - ч.1,2

7. Демидович Б.П. Сборник задач и упражнений по математическому анализу. – М.: Наука, 1977

8. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Наука, 1975

9. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, 1978

10. Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. – М.: ВШ, 1982. – ч.1,2

11. Колесников А.Н. Краткий курс математики для экономистов. – М.: ИНФРА-М, 1997

1. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1989

9. Малыхин В.И. Математика в экономике. – М.: ИНФРА-М, 2000

12. Мантуров О.В., Матвеев Н.М. Курс высшей математики. Линейная алгебра. Аналитическая геометрия. Дифференциальное исчисление функции одной переменной. – М.: ВШ, 1986

13. Мордкович А.Г., Солодовников А.С. Математический анализ. – М.: ВШ, 1990

14. Матвеев Н.М. Обыкновенные дифференциальные уравнения. – С.-П.: Спец. литература, 1996

15. Матвеев Н.М. Сборник задач и упражнений по обыкновенным дифференциальным уравнениям. – М.: ВШ, 1987

16. Пискунов Н.С. Дифференциальное и интегральное исчисление. – М.: Наука, 1988. – ч.1,2

17. Сборник задач по высшей математике для втузов, ч.1,2 / под ред. проф. Ефимова А.В., Демидовича Б.П.. – М.: ВШ, 1985

1. Справочник по математике для экономистов / под ред. проф.Ермакова В.И. – М.: Наука, 1986