Способ. Тригонометрическая подстановка

Теорема: Интеграл вида 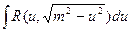подстановкой 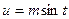или

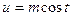сводится к интегралу от рациональной функции относительно sint или cost.

Пример:

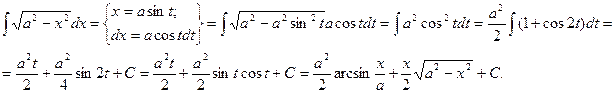
Теорема: Интеграл вида 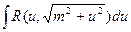подстановко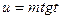й или 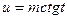сводится к интегралу от рациональной функции относительно sint и cost.

Пример:

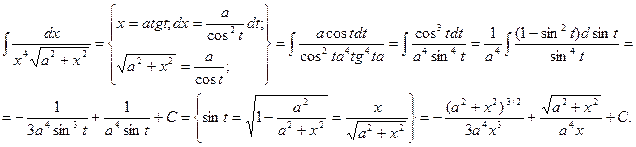
Теорема: Интеграл вида 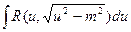подстановко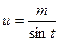й или 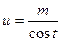сводится к интегралу от рациональной функции относительно sint или cost.

Пример:

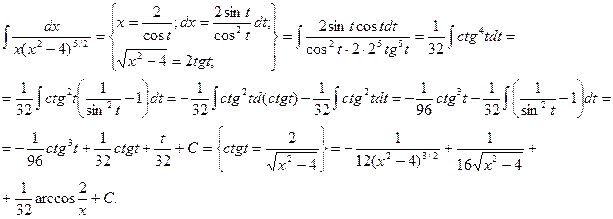
2 способ. Подстановки Эйлера.(1707-1783)

1) Если а>0, то интеграл вида 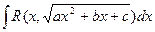рационализируется подстановкой

.

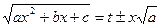2) Если a<0 и c>0, то интеграл вида 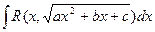рационализируется подстановкой .

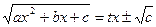3) Если a<0 , а подкоренное выражение раскладывается на действительные множители a(x – x₁)(x – x₂), то интеграл вида 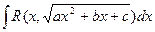рационализируется подстановкой .

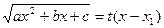Отметим, что подстановки Эйлера неудобны для практического использования,

т.к. даже при несложных подинтегральных функциях приводят к весьма громоздким вычислениям. Эти подстановки представляют скорее теоретический интерес.