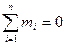Аналитические условия равновесия системы сходящихся сил.

Мы выяснили, что равнодействующая системы сил равна их геометрической сумме. Вычислим проекции выражения(1) на оси координат X,Y и Z.

R_X=P_1X+P_2X+…+P_NX=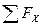

R_Y=P_1Y+P_2Y+…+P_NY=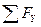

R_Z=P_1Z+P_2Z+…+P_NZ=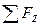

Где Fx, Fy и Fz проекции всех сил соответственно на оси X,Y и Z.

По проекциям определяем модуль равнодействующей и ее направление

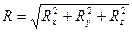
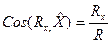
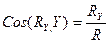
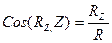
В случае если силы взаимно уравновешиваются, их равнодействующая R=0, следовательно равны нулю и суммы проекции всех сил.

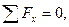
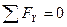
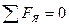(2)

Полученные уравнения называются аналитическими уравнениями равновесия пространственной системы сходящихся сил.Для сходящихся сил, расположенных в одной плоскости, получаем два уравнения равновесия

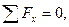
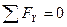(3)

Метод решения задач с помощью уравнений (2) и(3) называется аналитическими.

ТЕМА 3. ТЕОРИЯ ПАР СИЛ

Теория сил. Момент пары сил

Система двух равных по модулю, параллельных и противоположно направленных сил P и P¹ называется парой сил. Плоскость, в которой находятся линии действия сил Р и Р¹, называется плоскостью действия пары сил. (рис.17)

Пара сил не имеет равнодействующей , однако силы пары не уравновешиваются, так как они не направлены по одной прямой. Пара сил стремится произвести вращение твердого тела, к которому она приложена.пара сил, не имея равнодействующей, очевидно, не может быть уравновешена силой.

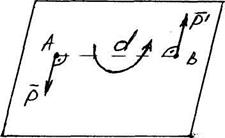Рис.17

Кратчайшее расстояние между линиями действия сил, составляющих пару, называется плечом пары сил.

Действие пары сил на твердое тело характеризуется ее моментом. Момент пары сил определяется произведением модуля одной из сил пары на ее плечо.

М= 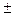P*d (4)

Момент пары считается положительным, если пара стремится вращать плоскость против хода часовой стрелки (рис.17), и отрицательным – по ходу часовой стрелки. Момент пары сил выражается в ньютонах-метрах (Н*м).

Эквивалентность пар сил.

Исходя из определения пары сил и ее момента, можно сделать ряд важных выводов.

Пары сил, расположенные в одной плоскости по своему действию на тело отличаются одна от другой только алгебраическим моментом. Две пары сил называются эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях, т.е. у пары сил можно менять плечо и силы, сохраняя при этом алгебраический момент. Причем, пару сил можно как угодно поворачивать и переносить не только в плоскости ее действия, но и в параллельную плоскость.

Векторный момент пары сил направлен перпендикулярно плоскости действия пары так, чтобы с его направления можно было видеть вращение пары против хода часовой стрелки.

Так как пару сил можно переносить в параллельную плоскость, то векторный момент пары сил можно переносить параллельно самому себе в любую точку тела, не изменяя действие пары сил на твердое тело. Поэтому векторный момент пары сил есть свободный вектор, т.е. он характеризуется только модулем и направлением, а точкой приложения у него может быть любая точка тела.

Следовательно, две пары сил, действующие на одно и тоже твердое тело, эквивалентны, если они имеют одинаковые по модулю и направлению векторные моменты.

Для того чтобы сложить несколько пар сил, необходимо найти такую ра­внодействующую пару сил, действие которой эквивалентно действию систе­мы пар сия Для этого необходимо:

а) на основании теоремы свойств эквивалентных пар привести все па­ры к одному плечу;

б) повернуть все пары так, чтобы линии действия сил были параллельны;

в) наложить все пары так, чтобы точки приложения сил, составляющих
пары сил, совпадали.

Для того чтобы тело под действием пар сил находилось в состоянии рав­новесия, необходимо и достаточно, чтобы момент равнодействующей пары или алгебраическая сумма моментов всех пар сил, приложенных к телу, рав­нялись бы нулю, т.е.