Исходные данные для расчетов. Для периодических сигналов и амплитудная, и фазовая характеристики всегда являются дискретными или линейчатыми
Амплитудные Фазовые
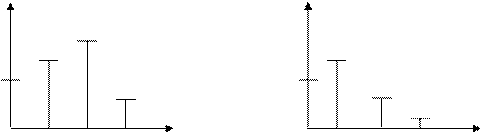 An Φn
An Φn
A2
A1 Φ1
A0 Φ0
A3 Φ2
Φ3
0 ω1 2ω1 3ω1 ωn 0 ω1 2ω1 3ω1 ωn
Для периодических сигналов и амплитудная, и фазовая характеристики всегда являются дискретными или линейчатыми.
Ряд Фурье в комплексной форме
Используя формулы Эйлера, можно получить другое симметричное и равноправное представление ряда Фурье – его комплексную форму:
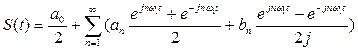 (8)
(8)
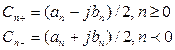 (9)
(9)
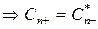 (10)
(10)
Подставляя (9) в (8), получаем ряд Фурье в комплексной форме:
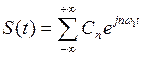 , (11)
, (11)
где 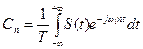 . (12)
. (12)
Между амплитудами гармоник тригонометрического ряда Фурье и коэффициентами его комплексной формы существует элементарная связь:
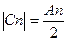 . (13)
. (13)
Энергия периодического сигнала в промежутке времени [t1, t2] на сопротивлении, равном 1 Ом, вычисляется по формуле:
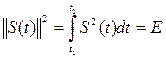 . (14)
. (14)
Среднюю мощность любого сигнала можно вычислить по формуле:
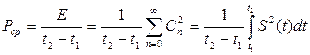 . (15)
. (15)
Таким образом, средняя за период мощность периодического сигнала:
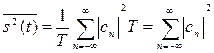 . (16)
. (16)
Используя тригонометрическую форму ряда Фурье и учитывая, что с0 = а0/2 и 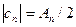 , получаем
, получаем
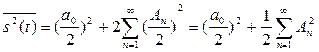 (17)
(17)
Если s(t) представляет собой ток i(t), то при прохождении его через сопротивление r выделяется мощность (средняя)
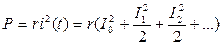 , (18)
, (18)
где I0 – постоянная составляющая тока.
Задание.Для предложенных в соответствии со своим вариантом видов сигналов:
1. Записать ряд Фурье в тригонометрической и комплексной форме.
2. Составить общие выражения для расчета тригонометрических и комплексных амплитуд и фаз гармонических составляющих данных сигналов.
3. Найти значения амплитуд и фаз первых пяти гармоник для конкретных заданных параметров анализируемых сигналов.
4. Построить графики амплитудного и фазового спектров.
5. Определить полную (среднюю за период) мощность данных сигналов и мощности, приходящиеся на постоянную составляющую и каждую из первых пяти гармоник.
6. Найти эффективную ширину спектра, в которой сосредоточено 90% полной мощности данных сигналов.
Исходные данные для расчетов.
1. Меандр: а) четный, б) нечетный.
2. Пилообразное колебание.
3. Гармоническое колебание: a) s(t) = Е /cos(pt/T)/; б) s(t) = Е /sin (pt/T)/.
4. Последовательность: а) четная; б) нечетная – прямоугольных униполярных импульсов.
| Варианты/ Параметры | |||||||
| Амплитуда, В | |||||||
| Период, мс | |||||||
| Длительность импульса, мс | 0,5 | 0,5 |
Контрольные вопросы:
1. Каков физический смысл постоянной составляющей периодического сигнала?
2. Существует ли различие между спектральными диаграммами периодического сигнала при использовании амплитуд гармоник тригонометрического ряда Фурье и коэффициентов комплексного ряда? Если да, то в чем оно проявляется?
3. Каковы размерности амплитудного и фазового спектров периодических сигналов?
4. Каков физический смысл квадрата нормы функции сигнала?
5. Отличаются ли между собой амплитудные и фазовые диаграммы для четных и нечетных функций одинакового вида? Если да, то как?
6. Изменятся ли амплитудные и фазовые спектры при увеличении длительности импульсов, составляющих данную периодическую последовательность? Если да, то почему и как?
7. Почему спектральные диаграммы периодических сигналов всегда дискретны?
8. Зависит ли значение средней за период энергии сигнала от его положения на оси времени, четности или нечетности описывающей его функции?
9. Определите и поясните зависимость между изменением длительности импульсов, составляющих периодическую последовательность, и количеством гармоник, приходящихся на эффективную ширину спектра сигнала.
