Описание установки и вывод расчетной формулы. В комплект лабораторной установки входят маятник (рисунок 2), секундомер, мерная линейка

В комплект лабораторной установки входят маятник (рисунок 2), секундомер, мерная линейка.

Чечевицу 2 можно передвигать по стержню и фиксировать с помощью винта. Для определения ее положения на конце стержня нанесены миллиметровые деления 1. Опорные призмы 3 и 7 закреплены на стержне 5 жестко.

На рисунке 2 приведено одно из положений маятника. При этом маятник будет колебаться относительно призмы 3. Можно перевернуть маятник и установить призму 7 в канавку 4. Если передвигать чечевицу 2 по стержню, то изменится положение точки C – центра масс маятника, а, следовательно, и период колебаний.

Исходя из (1) период колебаний маятника на ребре призмы (оси) А выразится:

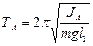, (2)

а период колебаний на ребре призмы (оси) B:

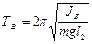, (3)

где J_А – момент инерции маятника относительно оси A ;

J_B – момент инерции маятника относительно оси B.

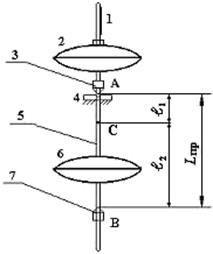
Рисунок 2 Схема подвешенного оборотного маятника:

1 – миллиметровая шкала; 2 – подвижная чечевица;

3, 7 – опорные призмы; 4 – опорная канавка; 5 – стержень;

6 – неподвижная чечевица

На рисунке приняты обозначения: С – центр масс маятника; l₁ – расстояние между ребром А и точкой С; l₂ – расстояние между ребром В и точкой С

Преобразуем (2) и (3), используя теорему Штейнера, которая для колебаний на ребре призмы A записывается как

J_A = J_C + m_C l₁2, (4)

и гласит: момент инерции маятника относительно ребра призмы А равен сумме момента инерции маятника относительно центра масс C (J_C) и произведения массы на квадрат расстояния от оси вращения до центра масс C (m_C l₁2 ).

Теорема Штейнера для колебаний маятника относительно ребра призмы B записывается в виде

J_B = J_C + m_C l₂2 , (5)

где l₂ - расстояние междуребром B и центром масс C; J_C - момент инерции оборотного маятника относительно центра масс C.

Определение величины J тела сложной формы, такого как оборотный маятник, является трудной задачей. Поэтому преобразуем зависимости моментов инерции так, чтобы исключить величину J_C .

Перепишем формулы (2) и (3) с учетом выражений (4) и (5)

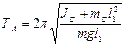, (6)

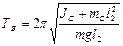_. (7)

Для решения нашей задачи найдем такое положение чечевицы 2, что будет выполняться условие

T_А = T_В = T₀ . (8)

Подставим (6) и (7) в условие (8): .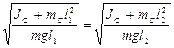

Отсюда получаем

J_C = m×l₁ l₂ . (9)

Выражение (9) подставим, например, в формулу (6) (или в (7))

_.

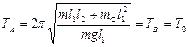Учтем, что m_C = m, тогда получаем

.

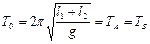Отсюда ускорение свободного падения тел ,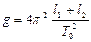

где, как видно из рисунка 2, l₁ + l₂ = L_пр (L_пр - приведенная длина оборотного маятника).

Таким образом, для вычисления ускорения свободного падения тел окончательно получаем

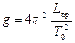_. (10)

Из (10) видно, что требуется найти экспериментально такие периоды колебаний маятника, чтобы выполнялось условие (8). Заметим, что добиться точного совпадения значений T_А и T_В практически невозможно. Приходится подбирать такое положение чечевицы 2, чтобы на призмах 3 и 7 оборотный маятник совершал колебания с приблизительно одинаковыми периодами T_А » T_В .