Задача об оптимальном составе сплава

Для получения сплавов А и В используются четыре металла I, II, III и IV. Характеристики и запасы руд, из которых получают эти металлы, указаны в табл. 48.

Требования к содержанию металлов I, II, III и IV в сплавах, а также стоимости одной тонны сплавов при продаже приведены в табл. 49.

Необходимо максимизировать прибыль от продажи сплавов А и В.

Таблица 48

Руда	Максимальный запас, тонны	Состав, %	Цена, доллары за тонну
I	II	III	IV	Другие компоненты

Таблица 49

Сплав	Требование к содержанию металла	Цена одной тонны сплава, в долларах
А	Не более 80% металла I
Не более 30% металла II
В	От 40% до 60% металла II
Не менее 30% металла II
Не более 70% металла IV

Решение включает этапы, описанные в пп. 3.2.2 -3.2.5.

Построение математической модели

1. Определение целевой функции

Обозначим количество металлов I, II, III и IV, использованных для получения сплава А, переменными Х_1А, Х_2А, Х_3А, Х_4А. Количество металлов I, II, III и IV, использованных для получения сплава В, обозначим переменными Х_1В, Х_2В, Х_3В, Х_4В.

Для обозначения количества используемой руды введем переменные Y₁, Y₂, Y₃.

Объем производимого сплава А (в тоннах) равен

Х_1А + Х_2А + Х_3А + Х_4А.

Аналогично объем сплава В равен

Х_1В + Х_2В + Х_3В + Х_4В.

Прибыль от продажи сплава А составит

Z₁ = 200 (Х_1А + Х_2А + Х_3А + Х_4А), (16)

а прибыль от продажи сплава В равна

Z₂ = 210 (Х_1В + Х_2В + Х_3В + Х_4В). (17)

Стоимость руд, использованных при литье металлов, равна

Z₃ = 30 Y₁ + 40 Y₂ + 50 Y₃. (18)

Тогда целевую функцию – прибыль предприятия – можно записать в виде разности между прибылью от продажи сплавов и затратами на руды

Z = Z₁ + Z₂ - Z₃. (19)

Или, подставляя выражения (16), (17) и (18) получим

Z = 200 (Х_1А + Х_2А + Х_3А + Х_4А) + 210 (Х_1В + Х_2В + Х_3В + Х_4В) -30 Y₁-40 Y₂ – 50 Y₃ (20).

2. Определение ограничений на переменные

Можно выделить четыре вида ограничений:

а) По физическому смыслу переменных – объемы используемых металлов и руд не могут быть отрицательными, следовательно

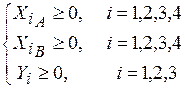(21)

б) Ограничения на состав сплавов. Согласно табл.49, получаем

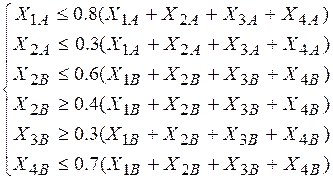(22)

в) Ограничения на состав металлов согласно табл. 48:

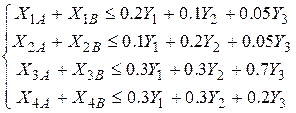(23)

г) ограничения по запасам руды:

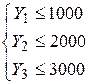(24)

Итак, для решения задачи нужно найти такие значения расходуемых объемов металлов Х_1А, Х_2А, Х_3А, Х_4А, Х_1В, Х_2В, Х_3В, Х_4В и руд Y_1, Y₂, Y₃, которые обеспечат максимальное значение целевой функции (20) при выполнении ограничений (21) – (24).

Построение начального плана решения

1. Отведем под переменные Х_1А, Х_2А, Х_3А, Х_4А диапазон ячеек В4:В7 электронной таблицы (в табл. 50 ЭТ приведена в режиме показа вычислений, в табл. 51 – в режиме показа формул Excel, в табл. 52 – показа формул в Calc).

Таблица 50

A

B

C

D

E

F

G

H

I

J

K

Оптимальный состав сплава

Сплав

Металл

А

В

Руда

Состав металлов

Номер

Затраты

Запас

Цена

I

II

III

IY

0,2

0,1

0,3

0,3

0,1

0,2

0,3

0,3

0,05

0,1

0,7

0,2

Ограничения

Левая часть

Правая часть

Целевая функция

2. Для хранения переменных Х_1В, Х_2В, Х_3В, Х_4В отведем диапазон ячеек С4:С7 электронной таблицы.

3. В ячейках Е5:Е7 разместим значения переменных Y_1, Y₂, Y₃. Для всех переменных начальные значения полагаем равными нулю.

4. В диапазоне ячеек F5:F7 вводим значения имеющихся запасов руды из второго столбца табл. 48.

5. В диапазон ячеек G5:G7 вводим цены за одну тонну руды из последнего столбца табл. 48.

6. В диапазон ячеек Н5:К7 помещаем характеристики состава руд из столбцов 3 – 6 табл. 49.

7. В ячейки диапазона А10:А15 вводим левые части ограничений (22).

8. В ячейки диапазона Е10:Е15 вводим правые части ограничений (22).

9. В ячейки диапазона А16:А19 вводим левые части ограничений (23).

10. В ячейки диапазона Е16:Е19 вводим правые части ограничений (23).

11. В ячейке А21 размещаем целевую функцию (20).

Оптимизация плана решения

1) Вызываем режим Поиск решения (Сервис – Поиск решения).

2) Заполняем окно Поиск решения (рис. 14а для Excel и 14б для Calc).

3) Командой Выполнить запускаем режим Поиск решения.

Результат его работы представлен в табл. 53.

Таблица 51

	A	B	C	D	E	F	G	H	I	J	K
	Оптимальный состав сплава
		Сплав
	Металл	А	В	Руда	Состав металлов
				Номер	Затраты	Запас	Цена	I	II	III	IY
								0,2	0,1	0,3	0,3
								0,1	0,2	0,3	0,3
								0,05	0,05	0,7	0,2
	Ограничения
	Левая часть	Правая часть
	=В4	=0,8*СУММ(В4:В7)
	=В5	=0,3*СУММ(В4:В7)
	=С5	=0,6*СУММ(С4:С7)
	=С5	=0,4*СУММ(С4:С7)
	=С6	=0,3*СУММ(С4:С7)
	=С7	=0,7*СУММ(С4:С7)
	=СУММ(B4:C4)	=СУММПРОИЗВ(E5:E7;H5:H7)
	=СУММ(B5:C5)	=СУММПРОИЗВ(E5:E7;I5:I7)
	=СУММ(B6:C6)	=СУММПРОИЗВ(E5:E7;J5:J7)
	=СУММ(B7:C7)	=СУММПРОИЗВ(E5:E7;K5:K7)
	Целевая функция
	=200*СУММ(B4:B7)+210*СУММ(C4:C7)-СУММПРОИЗВ(E5:E7;G5:G7)

В OpenOffice.org Calc строки 8-21 будут иметь вид табл. 52.

Таблица 52

	A	B	C	D	E	F	G	H	I	J	K
	Ограничения
	Левая часть	Правая часть
	=В4	=0,8*SUM(В4:В7)
	=В5	=0,3* SUM(В4:В7)
	=С5	=0,6* SUM(С4:С7)
	=С5	=0,4* SUM(С4:С7)
	=С6	=0,3* SUM(С4:С7)
	=С7	=0,7* SUM(С4:С7)
	=SUM(B4:C4)	=SUMPRODUCT(E5:E7;H5:H7)
	= SUM(B5:C5)	=SUMPRODUCTE5:E7;I5:I7)
	= SUM(B6:C6)	=SUMPRODUCT(E5:E7;J5:J7)
	= SUM(B7:C7)	=SUMPRODUCT(E5:E7;K5:K7)
	Целевая функция
	=200* SUM(B4:B7)+210*SUM(C4:C7)-SUMPRODUCT(E5:E7;G5:G7)

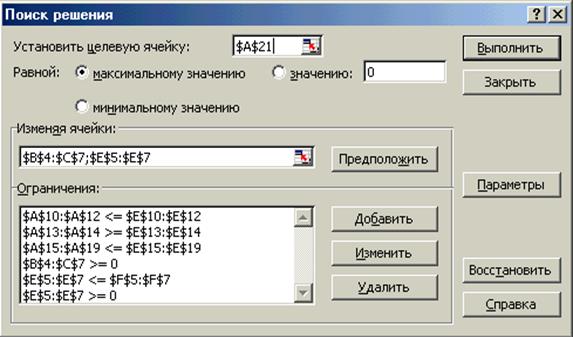
Excel Microsoft Office

Рис. 14а

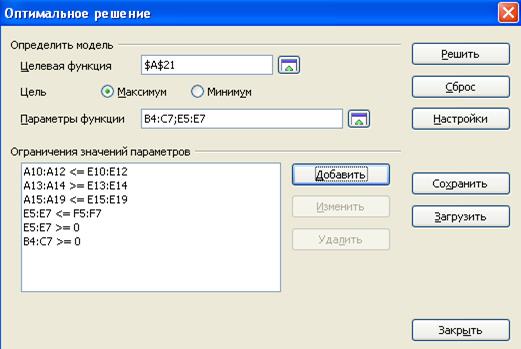
OpenOffice.org Calc

Рис. 14б

Таблица 53