Методика поиска оптимального дележа
1. Рассматриваются возможные коалиции и составляется первоначальный базовый дележ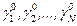 
. В дальнейшем значения 
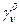по договоренности не изменяются.
2. Выигрыш каждого участника коалиции n в векторе дележа определяется по формуле Шепли
,
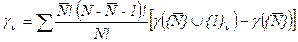где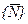 
-возможные коалиции без участника 
, 
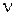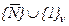-коалиции с участником .
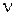3. Составляются вектора Шепли (ядра Шепли) рассмотренных коалиций, в которые включают только полезных участников.
4. Путём сравнения векторов находят оптимальный делёж (наилучшую коалицию).
Пример кооперативной игры
Пусть трем автомобилестроительным комбинатам необходим завод по выпуску шин. Строить завод можно на паях или отдельно каждому комбинату, например, по цеху. В этом случае возможны следующие коалиции участников:
- каждый комбинат строит завод в отдельности по цехам,
- строят часть завода на паях два комбината,
- строят весь завод на паях три комбината.
Расходы на строительство, затрачиваемые коалициями, (базовый дележ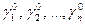 
) сведены в таблицу.
| Коалиции |  |  |  |  |  |  |  |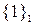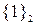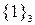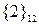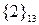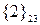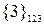
| Стоимость работ |
Из анализа дележа следует, что все участники полезные, так как затраты при индивидуальном строительстве 
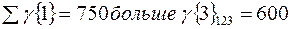
Рассчитаем сумму взносов на строительство каждого из участников в других коалициях.
1. Коалиция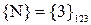 
.
Определим сумму взносов в млн. руб. 1-го участника по формуле Шепли
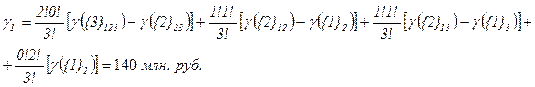
Аналогично определим сумму взносов 2-го и 3-го участников:
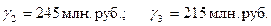
Общая сумма взносов
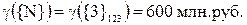
2. Коалиции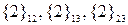 
. По формуле Шепли определяем сумму взносов участников в коалиции в млн. руб.
Для коалиции :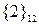 
, 
,
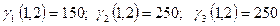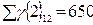для коалиции :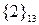 
, 
,
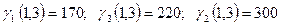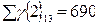для коалиции :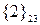 
, 
.
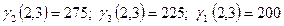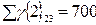Из сравнения полученных дележей (сумм взносов на строительство) следует, что наилучшая (справедливая) коалиция 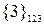, имеющая дележ
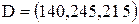. При этом каждый из участников, вступая в такую коалицию, по сравнению с индивидуальным строительством будет иметь соответственно выигрыш 60 млн. руб., 55 млн. руб., 35 млн. руб.
Литература
1. Коршунов Ю.М. Математические основы кибернетики. Учеб. пособие. М.: Энергия, 1972.
2. Волков И.К., Загоруйко Е.А. Исследование операций. Учеб. пособие. М.: Издательство МГТУ им. Баумана, 2002.
CОДЕРЖАНИЕ
| Введение | |
| 1. Основы оптимизации процессов управления…………………..… | |
| 1.1. Математическое описание объекта….………………………….. | |
| 2. Одношаговые задачи управления………………………………..... | |
| 2.1.Линейное программирование……………………………………. | |
| 2.2. Двойственная задача линейного программирования | |
| 3. Многошаговые процессы управления……………………………. | |
| 3.1. Динамическое программирование……………………………… | |
| 4. Игровые задачи управления………………………………………. | |
| 4.1. Основы игровых задач…………………………………………… | |
| 4.2. Кооперативные игры…………………………………………….. | |
| Литература……………………………………………………………... |
D:\Kafedra\Morozov\Комплекс Математические основы
оптимального управления 2014
Состав курса:
| Очное отделение: 1. Лекций, ч. – 16 2. Упражнений, ч. – 16 3. Аттестация – зачет 4. Семестр – 2(уск.), 3 | Заочное отделение: 1. Лекций, ч. – 4 (5-ти л.), 2 (4-х. л.) 5. Упражнений, ч. – 6 (5-ти л.), 4 (4-х. л.) 2. Контрольная работа 3. Аттестация – зачет 4. Семестр – 4 |