Р е ш е н и е. Текстовая задача равносильна смешанной задаче

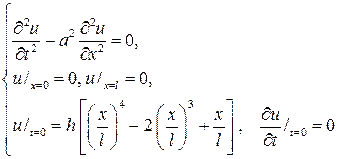
Подставив u(x,t)=X(x)T(t) в дифференциальное уравнение, получим

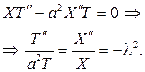
Из граничных условий найдем

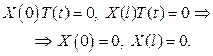
Решаем задачу Штурма Лиувилля:

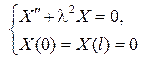
Общее решение

,

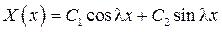из граничных условий следует .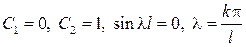

Собственные функции имеют вид .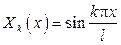

Из дифференциального уравнения 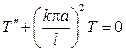следует, что

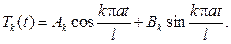
Возьмем теперь функциональный ряд

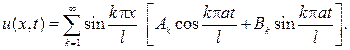
Подставляя его в первое начальное условие, получим

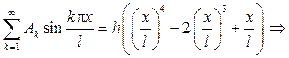
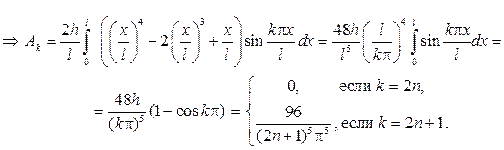
При вычислении интеграла применялось интегрирование по частям, причем вне интегральные слагаемые обращались в нуль на каждом шаге.

Из второго начального условия имеем

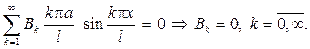
Подставляя найденные коэффициенты в функциональный ряд, придем к ответу

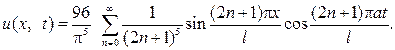
145.Труба, открытая с одного конца, движется поступательно в направ- лении своей оси с постоянной скоростью v . Вмомент t=0труба мгновен- но останавливается. Определить смещение воздуха внутри трубы на рас- стоянии х от ее закрытого конца.

Р е ш е н и е. Текстовая задача приводится к смешанной задаче

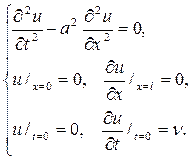
Полагая u(x,t)=X(x)T(t), получим после подстановки в дифферен-циальное уравнение и разделения переменных

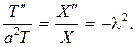
Из граничных условий найдем

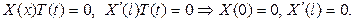
Присоединяя полученные граничные условия к дифференциальному уравнению для функции Х(х) придем к задаче Штурма Лиувилля:

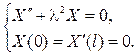
Необходимо найти ее собственные значения и собственные функции. Подставляя общее решение 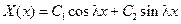в первое из граничных условий, будем иметь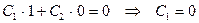

Считая С₂=l, из второго граничного условия найдём

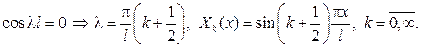
Дифференциальное уравнение для функции Т(t) будет иметь вид

,

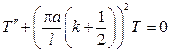и его общее решение

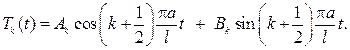
Cогласно схеме метода Фурье, перемножаем T_k(t) на собственные функции 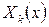и составляем ряд

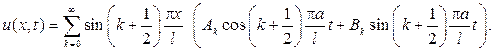
Подставив в первое начальное условие, получим

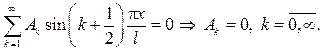
Из второго начального условия найдем

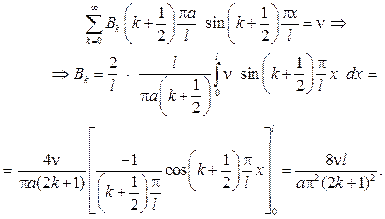
С учетом найденных значени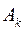й и 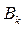придем к ответу

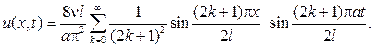
146. Найти продольные колебания упругого стержня, один конец ко- торого 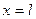закреплен жестко, а другой х=0 свободен, при начальных ус- ловиях

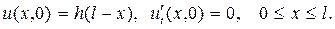
Р е ш е н и е. Отклонение точек стержня 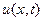от положения равнове -сия будет решением смешанной задачи

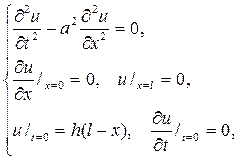
которую решаем по методу Фурье, полагая u(x,t)=X(x)T(t).

После разделения переменных получим два обыкновенных дифферен- циальных уравнения с параметром :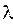

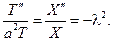
Из граничных условий найдем

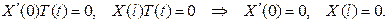
Теперь решаем задачу Штурма-Лиувилля

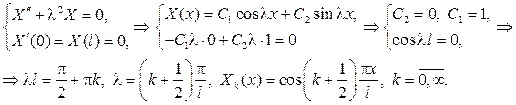
Из дифференциального уравнения для функции T(t) найдем

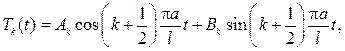
и решение смешанной задачи разыскиваем в виде ряда

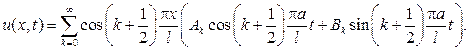
Подставляя этот ряд в первое начальное условие, будем иметь

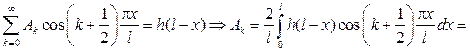
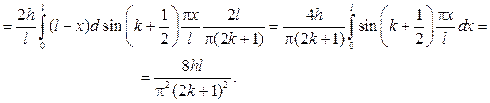
Из второго начального условия получим

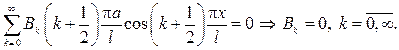
Подставляя найденные коэффициенты в ряд, придем к ответу

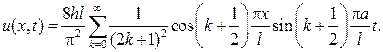
147. Найти продольные колебания упругого стержня со свободными концами х=0и 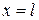при начальных условиях

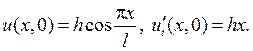
Р е ш е н и е. Отклонение точек стержня u(x,t) от положения равнове -сия будет решением смешанной задачи для однородного уравнения коле -баний струны

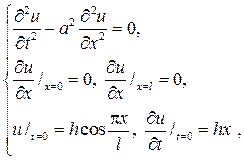
которую решаем методом Фурье, полагая u(x,t)=X(x)T(t). После подста- новки в дифференциальное уравнение и разделения переменных найдем опять таки

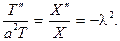
Из граничных условий на этот раз получим

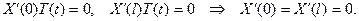
Теперь находим собственные значения и собственные функции задачи Штурма Лиувилля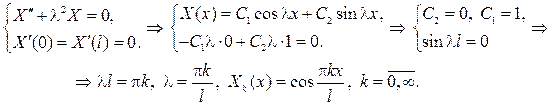

Решая дифференциальное уравнение для функции T(t), будем иметь

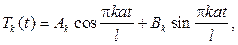
и, следовательно, для смешанной задачи нужно составить ряд

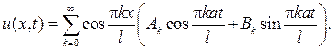
Подставляя его в первое начальное условие, получим

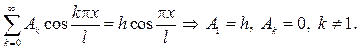
Из второго начального условия найдем

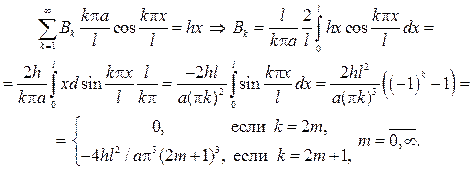
Подставляя значения коэффициентов в ряд, придем к ответу

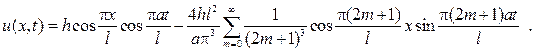
148.Один конец х=0 стержня свободен, а другой 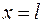закреплен упруго. Найти продольные колебания стержня при начальных условиях

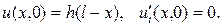
Решение. Здесь нужно решать смешанную задачу

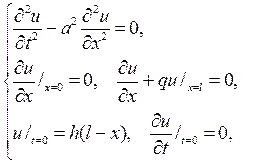
методом разделения переменных, полагая u(x,t)=X(x)T(t).

После разделения переменных придем к двум обыкновенным диффе- ренциальным уравнениям:

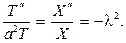
Из граничных условий найдем

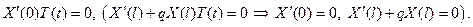
Теперь решаем задачу Штурма-Лиувилля:

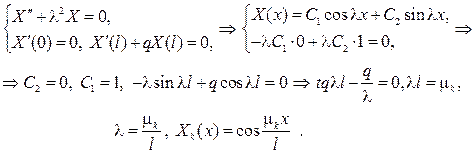
Обозначим через 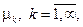положительные корни уравнения

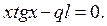
Из дифференциального уравнения для функции Т(t)найдем

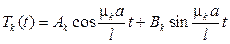
и решение смешанной задачи разыскиваем теперь в виде ряда

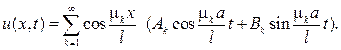
Подставляя этот ряд в первое начальное условие, получим

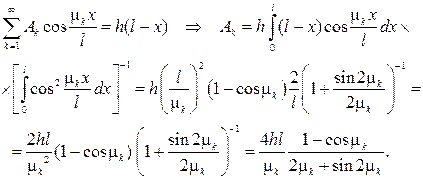
Из второго начального условия найдем, что 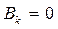, следовательно при- дем к ответу

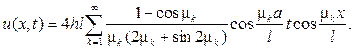
149.Однородная струна, закрепленная на концевых точках x=0и х=l, имеет в начальный момент времени форму параболы, симметричной относительно прямой 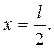Определить смещение точек струны u=u(x,t) от прямолинейного положения равновесия, предполагая, что начальные скорости равны нулю.

150.Однородная струна длиной l натянута между точками х=0и x=l. В точке x=l/2струна отклонена на небольшое расстояние h от положения равновесия и в момент t=0 отпускается без начальной скорости. Определить отклонение u(x,t)струны при t>0.

151.Однородная струна длиной l закреплена на конце x=0, а к другому ее концу прикреплено кольцо, массой которого можно пренебречь. Кольцо может скользить по гладкому стержню, оно отклонено на малое рассто- яние h от положения равновесия и в момент t=0 отпущено. Найти u(x,t) при t>0.

Решите следующие смешанные задачи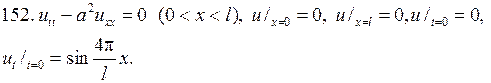

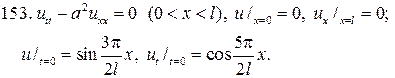
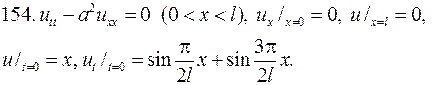
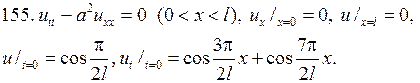
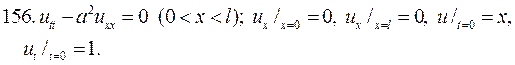
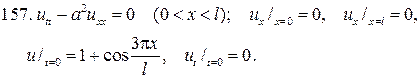
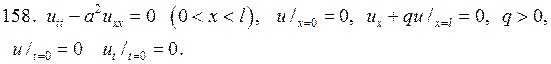
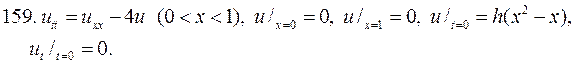
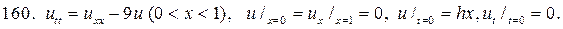
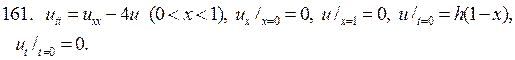
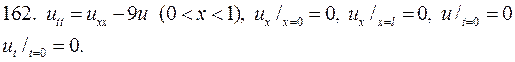
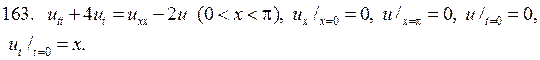
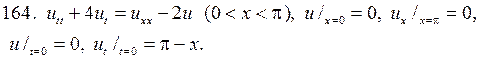
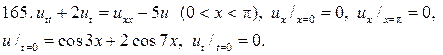
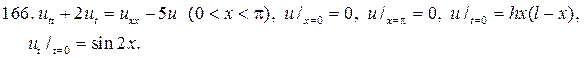
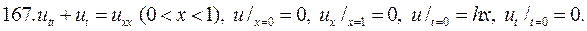
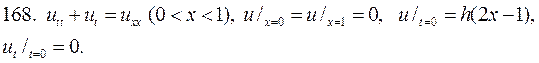
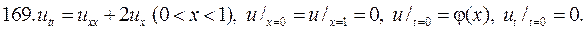
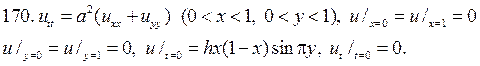
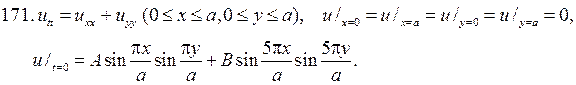
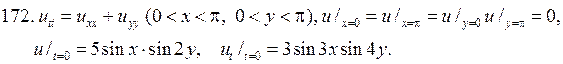
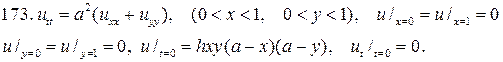
РЕШЕНИЕ СМЕШАННОЙ ЗАДАЧИ