Следствия из второго свойства пары

1. Действие пары на твердое тело не изменяется, если пару сил поворачивают в плоскости пары. Очевидно, что при этом момент пары не изменяется.

2. Действие пары сил на твердое тело не изменяется, если пару сил переносят в другое место плоскости пары. Это соответствует переносу момента пары, как свободного вектора, параллельно плоскости пары.

3. Действие пары сил на твердое тело не изменяется, если ее перенести в плоскость, параллельную плоскости пары. То есть момент пары, как свободный вектор, переносится перпендикулярно плоскости пары.

Эти на первый взгляд парадоксальные свойства пары сил поясним физическими примерами. Гаечный ключ одинаково действует на гайку, к каким бы граням этой гайки его не приложить - момент пары не изменяется от поворота пары сил в плоскости пары. Трансмиссионный вал передает шкиву вращающий момент независимо от места закрепления шкива на валу - момент пары сил не изменяется от ее переноса в плоскость, параллельную плоскости пары.

Моменты пар рассматриваются как векторы, когда пары сил лежат в различных плоскостях. В плоской системе сил, когда все силы и пары сил лежат в одной плоскости, моменты пар направлены перпендикулярно этой плоскости и поэтому параллельны друг другу. Естественно, что в этом случае, момент пары удобнее рассматривать как алгебраическую величину, равную

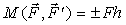(6)

Момент пары будет положительной величиной, если пара сил стремиться повернуть тело против хода часов и отрицательной, если она поворачивает тело по ходу часов.

Эквивалентность пар сил. Две пары сил с равными моментами эквивалентны. Или (F,F') ~ (P,P') , если M(F,F') ~ M(P,P'). Эквивалентность пар сил сразу следует из свойств пары сил. Очевидно, что только при равных моментах пар сил их действие на твердое тело будет одинаковым.

Следует отметить, что силы, образующие пары могут быть не равны между собой F 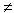P, но обе пары сил должны лежать в одной плоскости. Это замечание и понятие эквивалентности пар сил позволяют сформулировать правило трансформирования пары сил.

При трансформировании пары сил можно менять величины сил и плечо пары так, чтобы величина момента пары не изменялась, и переносить пару сил согласно следствиям из 2-го свойства.

Система пар сил.

Системой пар сил является совокупность пар сил, приложенных к одному телу.

Сложение пар сил. Система пар сил эквивалентна одной паре, момент которой равен сумме моментов пар, образующих систему:

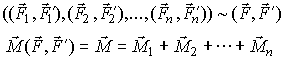(8)

где M₁ = M(F₁,F₁'), M₂ = M(F₂,F₂'), ..., M_n = M(F_n,F_n').

Моментом пары сил называется взятое со знаком (+) или (-) произведение величины одной из сил на ее плечо: m = ±Pd. Момент пары считается положительным, если пара стремится вращать тело против вращения часовой стрелки. Пару сил принято изображать изогнутой стрелкой (фиг.30, б). Буква у конца стрелки обозначает момент пары.

Условие равновесия пар: для равновесия нескольких пар необхо­димо и достаточно, чтобы алгебраическая сумма их моментов была равна нулю.

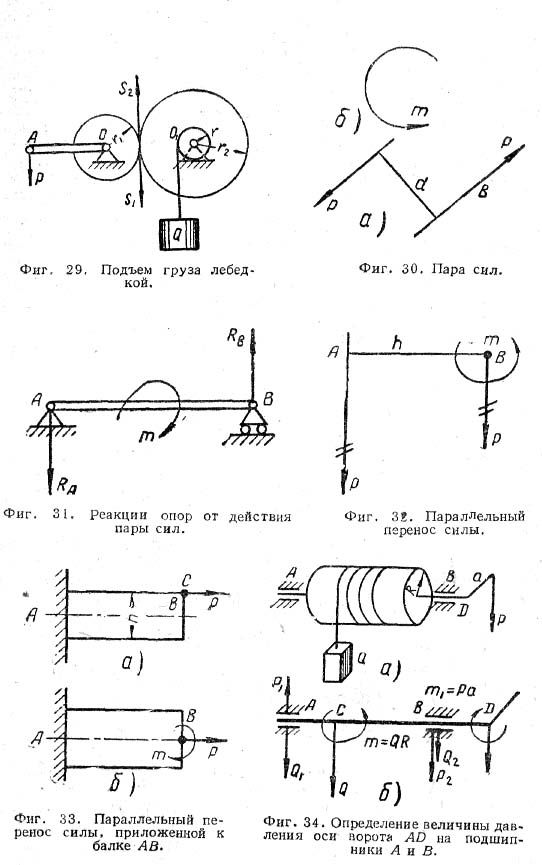
Момент пары сил не имеет точки приложения (Вторая теорема Вариньона): к каким бы частям твёрдого тела ни прикладывались силы, при данных величине и направлении момента сил вращаться оно будет одинаково.

Действие силы, приложенной к твёрдому телу на некотором расстоянии d от центра масс (в точке, в которую из центра масс можно провести вектор 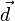), эквивалентно дествию такой же силы, приложенной непосредственно к центру масс, комбинированной с некоторой парой сил, такой, что 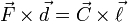, то есть с моментом, равным моменту силы относительно центра масс (в частности, если 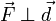, можем задаться 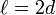, в таком случае одна из сил будет приложена в той же точке, что и исходная, и составит ).

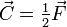11.Теорема об эквивалентности пар сил. Пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющий одинаковый с первой парой момент.

Доказательство: Пусть на твердое тело действует пара сил .

Перенесем силу в точку , а силу в точку . Проведем через точки две любые параллельные прямые, пересекающие линии действия сил пары. Соединим точки отрезком прямой и разложим силы в точке и в точке по правилу параллелограмма.

Так как , то

и

Поэтому эквивалентна системе , а эта система эквивалентна системе , так как эквивалентна нулю.

Таким образом мы заданную пару сил заменили другой парой сил . Докажем, что моменты у этих пар сил одинаковы.

Момент исходной пары сил численно равен площади параллелограмма , а момент пары сил численно равен площади параллелограмма . Но площади этих параллелограммов равны, так как площадь треугольника равна площади треугольника .

Что и требовалось доказать.

Выводы:

1. Пару сил как жесткую фигуру можно как угодно поворачивать и переносить в ее плоскости действия.

2. У пары сил можно изменять плечо и силы, сохраняя при этом момент пары и плоскость действия.

14.